数学分析：多元微积分2
这是内积的概念，经常说的欧几里得空间。
这是一个非常重要的概念，我们是根据不等式，然后引入了向量之间的夹角的概念。
同时我们需要证明几何上的向量之间的夹角和我们内积空间下的夹角是一样的。
上述都可以较好的证明两者的等价性：
请教内积公式A·B=|A||B|cosθ是怎么推导出来的？ - 知乎
用向量证明余弦定理是否存在逻辑错误？ - 知乎
这个定理叫做里斯表示定理，在《线性代数应该这样学》的内积章节里面有证明。这个非常重要，将是我们解开多元微积分里的一个重要的钥匙。
这里我们就要开始适应多元微积分的概念，这里的f'(x)并不是一个斜率，而是一个矩阵，是一个线性映射。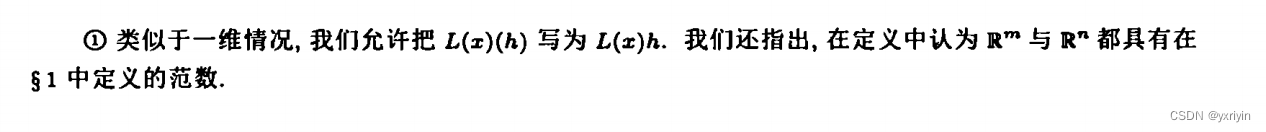
这段话要好好理解，向量h是点x上的切空间里的向量，它上面的微分值是f(x)里的切空间里的向量。所以f'(x)的线性映射就是x的切空间到f(x)的切空间的映射。
这里的4就是利用了里斯表示定理。
这样我们就十分自然的得到了全微分公式，多元微分公式也在此。
要注意，这里的偏导依然是一个线性映射，是一个矩阵。
这个是多元函数下自变量的微分等于自变量的增量的一个推倒过程。
首先
而
这是微分的定义 ,所以我们根据(8)可以得到(9).
终于，我们得到了这个雅克比矩阵。要注意我们的思路：
首先我们把映射f拆成多个(f1,f2,....fn),这样每个映射都可以用里斯表示定理，得到偏导数的求和形式，然后再展开成两个矩阵的乘积。
确实太妙了。
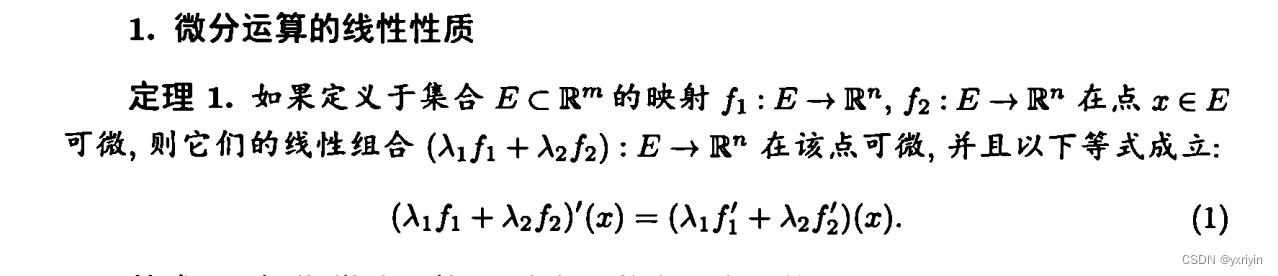
微分运算具有线性性质。
一个线性映射就对应一个雅克比矩阵。