题目 

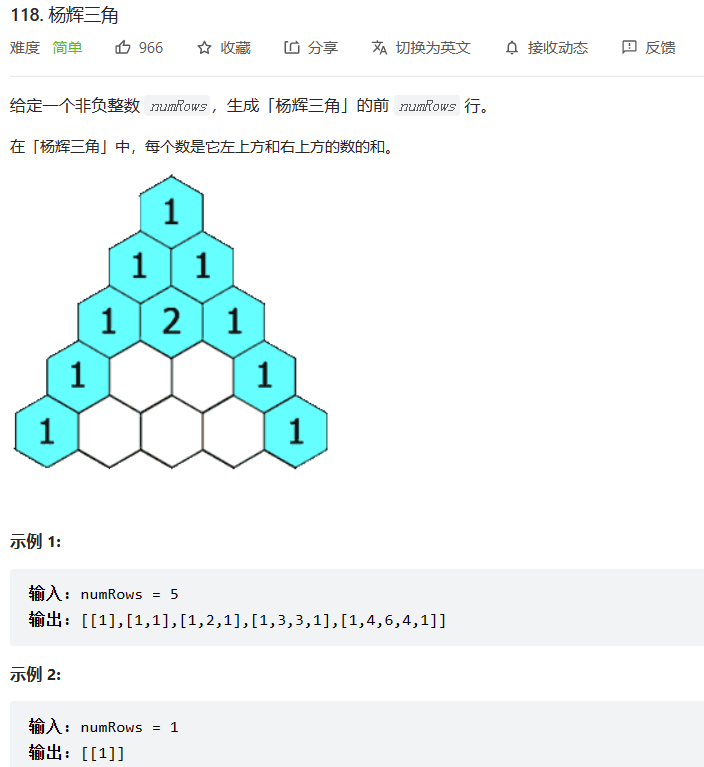
118. 杨辉三角 - 力扣（LeetCode）

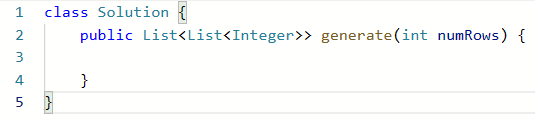
 可以看到，默认的代码块中出现List<List<Integer>>为二级ArrayList，类似于数组中的二维数组。List<元素类型>

在List<List<Integer>>中，元素类型为List<Integer>；

在List<Integer>中，元素类型为Integer。

即每一行为一个线性表，线性表中的元素为Integer类型，最终的杨辉三角也是一个线性表，元素类型为每一行的线性表。

思路 

 接下来，我们分析一下题目：

1.在杨辉三角中，第一行只有一个元素，为数字1；

2.第二行只有两个元素，均为1；

3.第三行有三个元素，为1,2,1（中间的数字2为上一行的两个1相加得到）；

4.第四行有四个元素，为1,3,3,1（从第三行开始，需要运算得到的数为当前行数的下标－1，即内层循环为j < i）； 

.......

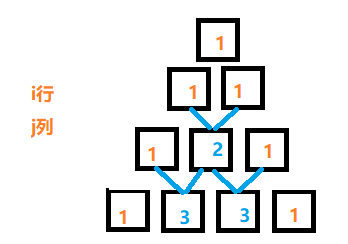
 假设我们有i行，j列，那么每一行的第一个元素和最后一个元素均为1，且第i行的第j个元素就等于i-1行的第j个元素和第j-1个元素之和。

即array[ i ][ j ] = array[ i - 1 ][ j ] + array[ i - 1 ][ j - 1 ]

完整代码

class Solution {public List<List<Integer>> generate(int numRows) {//根据题目已知，numRows为行数if(numRows == 1){//构建一个新的线性表用来存放最终的结果List<List<Integer>> ans = new ArrayList<>();//构建一个新的线性表用来存放每一行的元素List<Integer> row = new ArrayList<>();//将元素1放入第一行中row.add(1);//将第一行放入最终的线性表中ans.add(row);return ans;}if(numRows == 2){//有两行时，先把第一行的线性表加入，再将第二行的线性表加入List<List<Integer>> ans = new ArrayList<>();List<Integer> row = new ArrayList<>();row.add(1);     ans.add(row);   //第一行的线性表加入到最终的线性表中row = new ArrayList<>();row.add(1);row.add(1);ans.add(row);   //第二行的线性表加入到最终的线性表中return ans;}//从第三行开始，中间的元素需要经过运算得出List<List<Integer>> ans = new ArrayList<>();List<Integer> row = new ArrayList<>();row.add(1);     ans.add(row);   //第一行的线性表加入到最终的线性表中row = new ArrayList<>();row.add(1);row.add(1);ans.add(row);   //第二行的线性表加入到最终的线性表中//第三行开始下标为2for(int i = 2;i < numRows;i++){row = new ArrayList<>();row.add(1);List<Integer> lastRow = ans.get(i-1);    //得到上一行的元素for(int j = 1;j < i;j++){int a = lastRow.get(j);int b = lastRow.get(j - 1);row.add(a + b);}row.add(1); //将最后一个元素1放在整行最后ans.add(row);   //将这一行线性表加入到最终结果中    } return ans;}
}

代码优化

class Solution {public List<List<Integer>> generate(int numRows) {List<List<Integer>> ans = new ArrayList<>();List<Integer> row = new ArrayList<>();row.add(1);ans.add(row);if(numRows == 1){return ans;}row = new ArrayList<>();row.add(1);row.add(1);ans.add(row);if(numRows == 2){return ans;}//从第三行开始（下标为2）for (int i = 2; i < numRows; i++) {row = new ArrayList<>();row.add(1);       //添加每一行第一个元素为1List<Integer> lastrow = ans.get(i-1);   //得到上一行的元素//从每一行第二个元素开始（下标为1）//从第三行开始，需要运算得到的数为当前行数的下标－1for (int j = 1; j < i; j++) {int a = lastrow.get(j);int b = lastrow.get(j -1);row.add(a + b);}row.add(1);ans.add(row);}return ans;}
}