【轴承故障检测】滚动轴承中进行基于振动的故障诊断研究(Matlab代码实现)

💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
滚动轴承故障检测方法一般包括温度分析、油液分析以及振动信号检测等,通过不同的传感器的信号表现形式可以从不同角度分析轴承故障,通过多种方法的结合运用可以更加准确地判断轴承
故障。
本文可用于在匀速运行的滚动轴承中进行基于振动的故障诊断。
这是一个三步程序:(i)倒谱预白化:
减少其他周期性来源(如齿轮)的贡献。
(ii) 带通滤波:提高信噪比,特别是当对系统共振执行时 (iii) 平方包络频谱:允许检测
(伪)循环稳态贡献,其特征是在特定循环频率下具有大分量
此功能与一个简单的演示一起提供,并且与倍频程完全兼容。
📚2 运行结果
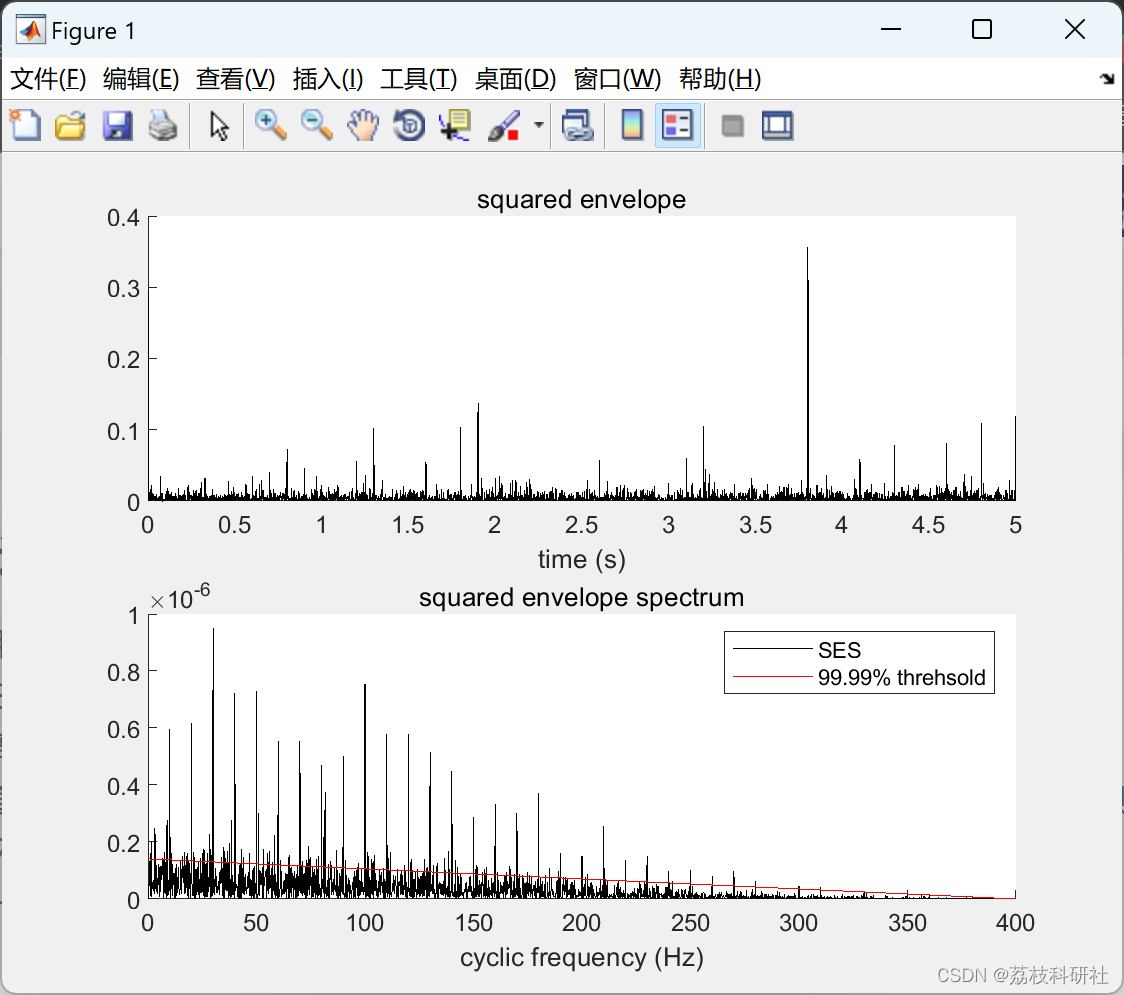
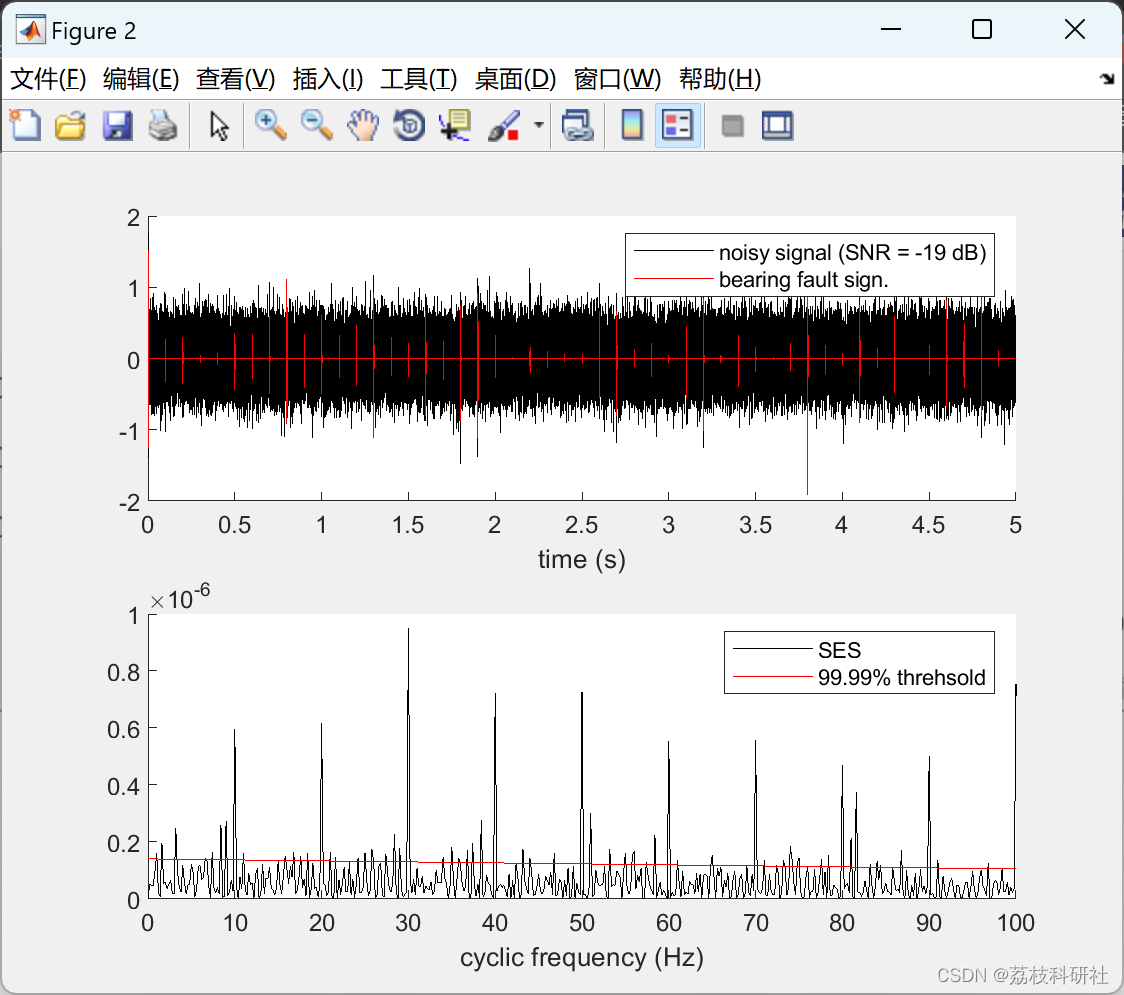
部分代码:
function [xSES,alpha,th] = SES(x,fs,bpf,plotFlag,p,cpswFlag)
%% Estimation of the Squared Envelope Spectrum
% this function can be used for detecting bearing faults under constant
% working speed
%
% INPUTS
% x = input signal
% fs = sampling frequency
% bpf = band-pass filter frequencies, use a vector as [f lower, f higher]
% put and empty vector if band-pass filtering is not needed
% bearing fault detection can be improved if performed in a frequency band
% wher the SNR is high (typically about a system resonance)
% plotFlag = display the SES, 0 -> no (default), 1 -> yes
% p = threshold significance level, default p = .999 (99.9%)
% cpswFlag = cesptrum pre-whitening, 0 -> no (default), 1 -> yes
% bearing fault detection is affected by periodic contribution due to
% external sources such as gears. This effect can be reduced by whitening
% the signal before SES
%
% OUTPUTS
% SES = squared envelope spectrum
% alpha = cyclic frequencies
% th = threshold
%
% REF: Borghesani P. et al, Application of cepstrum pre-whitening for the diagnosis of bearing
% faults under variable speed conditions, MSSP, 2013.
%
% M. Buzzoni
% May 2019
if nargin < 4
plotFlag = 0;
p = .999;
cpswFlag = 0;
end
if nargin < 5
p = .999;
cpswFlag = 0;
end
if nargin < 6
cpswFlag = 0;
end
L = length(x);
k = (0:L-1);
% cepstrum pre-whitening
if cpswFlag == 1;
x = real(ifft(fft(x) ./ abs(fft(x))));
end
% band-pass filtering and ses estimation
if isempty(bpf)
l = 1
h = floor(L/2)+1;
wfilt = zeros(size(x)); wfilt(l:h) = 1;
xf = ifft(2 .* fft(x) .* wfilt); % filtered analytic signal
else
l = floor(bpf(1)*L/fs); % lower freq. index
h = floor(bpf(2)*L/fs); % higher freq. index
wfilt = zeros(size(x)); wfilt(l:h) = 1;
xf = ifft(2 .* fft(x) .* wfilt); % filtered analytic signal
end
ENV = abs(xf).^2; % squared envelope
xSES = abs(1/L .* fft( ENV )) .^ 2; % squared envelope spectrum
% threshold
S0 = (h - l - k) ./ (2 * (h - l)^2 ) .* (mean(abs(xf).^2)).^2;
th = chi2inv(p,2) .* S0;
% keep only meaningful cyclic frequencies
alpha = k .* fs ./ L; % cyclic frequencies vector
alpha = alpha(1:h - l);
xSES = xSES(1:h - l); xSES(1) = 0; % put to zero the DC-term of SES in order to
th = th(1:h - l); % improve its visualization
if plotFlag == 1
% display results
tt = k ./ fs; % time vector
figure
subplot(211)
plot(tt,ENV,'k')
title('squared envelope')
xlabel('time (s)')
box off
subplot(212)
plot(alpha,xSES,'k')
title('squared envelope spectrum')
hold on, plot(alpha,th,'r')
legend('SES',[num2str(p .* 100) '% threhsold' ])
xlabel('cyclic frequency (Hz)')
box off
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]刁宁昆. 滚动轴承故障检测的无监督学习方法研究[D].石家庄铁道大学,2022.DOI:10.27334/d.cnki.gstdy.2022.000368.
[2]Borghesani P. et al, Application of cepstrum pre-whitening for the diagnosis of bearing faults under variable speed conditions, MSSP, 2013.

