D. Captain Flint and Treasure(拓扑排序 + 贪心)

Problem - D - Codeforces

芬特队长参与了另一个寻宝活动,但只发现了一个奇怪的问题。这个问题可能与宝藏的位置有关,也可能不是。这就是为什么弗林特船长决定把解决问题的工作交给他的船员,并提供了一个高得离谱的奖励:休息一天。问题本身听起来是这样的……有两个长度为n的数组a和b。最初,ans等于0,并定义如下操作:1. 选择位置i (1 <i<n);2. 在ans的基础上加上a;3.如果b, -1,那么加a;, abi对每一个i (1 Si S n)只执行一次,你能得到的最大ans是多少?Bogdan叔叔急于得到奖励,所以他请求你帮助他找到对他们进行手术的最佳位置顺序。输入第一行包含整数n (1 < n < 2-105) -数组a和b的长度。第二行包含n个整数a1, a2,…, an(-10°< a;< 106)。第三行包含n个整数b1 b2,。,bn (1 < bi < n or b;= 1)。附加约束:它保证对于任意i (1 < i< n)序列b, bbi>bb;?不是循环的,换句话说,它总是以-1结尾。输出在第一行中,打印您可以得到的最大ans。在第二行,打印操作顺序:n个不同的整数P1,P2,Pn (1 pi S n)。p是第i步应该选择的位置。如果有多个订单,打印其中任何一个。
Examples
input
Copy
3 1 2 3 2 3 -1
output
Copy
10 1 2 3
input
Copy
2 -1 100 2 -1
output
Copy
99 2 1
input
Copy
10 -10 -1 2 2 5 -2 -3 -4 2 -6 -1 -1 2 2 -1 5 5 7 7 9
output
Copy
-9 3 5 6 1 9 4 10 7 8 2
题解:
如果bi != -1,那么如果进行第i操作,abi += ai,bi可以看作一条i -> bi的边,
又说保证是不循环的,所以构建出来的图大概是这样
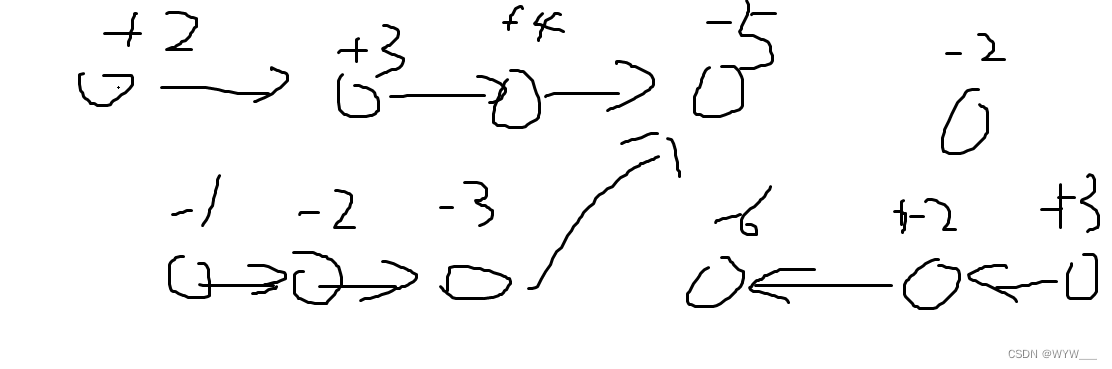
由于 abi += ai,是累加操作,ai的值会多次加上,所以,从叶子节点开始操作是最优的,
所以我们进行拓扑排序,每次把入度为0的点存入,并且如果ai >= 0让他的下一个节点+ai
对于叶子节点ai < 0的时候,累计会导致多次加上一个负数,肯定是不行的,所以我们
遍历到入度为0,的点并且ai<0,把它存到栈中
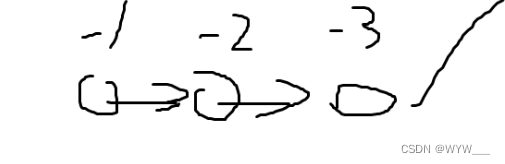
拓扑排序完拿的话,就变成了,先拿-3,然后-2,-1明显这是最优情况
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
#include<stack>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
#define int long long
vector<int> p[200050];
int a[200050];
int n;
int du[200050];
void solve()
{cin >> n;for(int i = 1;i <= n;i++){cin >> a[i];}for(int i = 1;i <= n;i++){int x;cin >> x;if(x != -1){du[x] ++;p[i].push_back(x);}}stack<int> s;queue<int> q;for(int i = 1;i <= n;i++){if(du[i] == 0)q.push(i);} vector<int> ans;int res = 0;while(q.size()){int t = q.front();q.pop();if(a[t] >= 0){ans.push_back(t);res += a[t];}elses.push(t);for(auto ne:p[t]){if(a[t] >= 0){a[ne] += a[t];}du[ne]--;if(du[ne] == 0){q.push(ne);}}}while(s.size()){int t = s.top();s.pop();res += a[t];ans.push_back(t);}cout << res <<"\\n";for(auto i:ans){cout <<i<<" ";}
}signed main()
{
// ios::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);int t = 1;
// cin >> t;while(t--){solve(); }
}

