概率密度函数的非参数估计方法

\\qquad 直接由样本来估计概率密度 p ( x ) p(\\boldsymbol{x}) p(x) 的方法,称为非参数方法 (non-parametric method) \\text{(non-parametric method)} (non-parametric method)。
\\quad
● \\quad 概率密度估计问题
( 1 ) (1) (1) 取自于概率密度 p ( x ) p(\\boldsymbol{x}) p(x) 的一个样本落在区域 R \\mathcal{R} R 中的概率为
P = ∫ R p ( x ) d x \\qquad\\qquad\\qquad P=\\displaystyle\\int_\\mathcal{R}p(\\boldsymbol{x})\\mathrm{d}\\boldsymbol{x} P=∫Rp(x)dx
概率 P i P_i Pi 对应于离散随机变量 X X X 取值为 x i x_i xi 的情形,即 P i = P ( X = x i ) P_i=P(X=x_i) Pi=P(X=xi)
连续随机变量用概率密度 p ( x ) p(\\boldsymbol{x}) p(x) 描述,概率 P = ∫ R p ( x ) d x P=\\int_\\mathcal{R}p(\\boldsymbol{x})\\mathrm{d}\\boldsymbol{x} P=∫Rp(x)dx 可看成是概率密度函数的 smoothed or averaged \\text{smoothed or averaged} smoothed or averaged的版本。
( 2 ) (2) (2) 假设基于概率密度 p ( x ) p(\\boldsymbol{x}) p(x) 独立同分布地抽取了 n n n 个样本 x 1 , x 2 , ⋯ , x n \\boldsymbol{x}_1,\\boldsymbol{x}_2,\\cdots,\\boldsymbol{x}_n x1,x2,⋯,xn,当 k k k 个样本落在区域 R \\mathcal{R} R 中,对概率 P P P 的一个较为合理的估计可表示为
k ≈ E [ Y ] = n P ⟹ P = k n \\qquad\\qquad\\qquad k\\approx E[Y]=nP\\quad\\Longrightarrow\\quad \\textcolor{crimson}{P=\\dfrac{k}{n}} k≈E[Y]=nP⟹P=nk
n n n 个样本中有 k k k 个落在区域 R \\mathcal{R} R 中属于“ n n n 重伯努利试验”:
(1) 样本落入区域 R \\mathcal{R} R 的次数 Y Y Y 是一个随机变量,服从二项分布 Y ∼ B ( n , P ) Y\\sim B(n,P) Y∼B(n,P),其中 P P P 为单个样本落入区域 R \\mathcal{R} R的概率
概率 p ( Y = k ) = C n k P k ( 1 − P ) n − k p(Y=k)=C_n^kP^k(1-P)^{n-k} p(Y=k)=CnkPk(1−P)n−k
(2) 求 Y Y Y 的数学期望可得到 E [ Y ] = n P E[Y]=nP E[Y]=nP
此外,对于二项分布 Y ∼ B ( n , P ) Y\\sim B(n,P) Y∼B(n,P) 而言, [ ( n + 1 ) P ] [(n+1)P] [(n+1)P] 是最可能出现的次数,也就是众数 (mode) \\text{(mode)} (mode),概率 p ( Y = k ) p(Y=k) p(Y=k) 的值在 [ ( n + 1 ) P ] [(n+1)P] [(n+1)P] 处达到最大(概率分布在此处出现波峰)
因此,可以认为 k ≈ n P k\\approx nP k≈nP 是一个较为合理的估计。
\\qquad 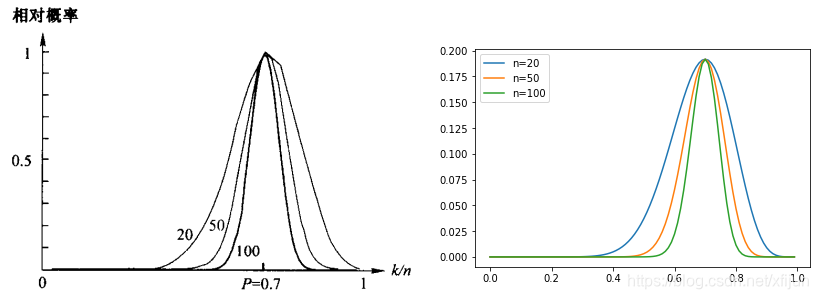
图1左图取自《模式分类》图4.1
三条曲线分别表示抽样数为 n = 20 , 50 , 100 n=20,50,100 n=20,50,100 时,二项分布 p ( Y = k ) = C n k P k ( 1 − P ) n − k ( k = 0.7 n ) p(Y=k)=C_n^kP^k(1-P)^{n-k}\\ (k=0.7n) p(Y=k)=CnkPk(1−P)n−k (k=0.7n) 在不同的 P P P 处的值(纵轴都进行了尺度调整)
抽样点数 n n n 越大, p ( Y = k ) p(Y=k) p(Y=k) 的值越容易在真实概率 P = 0.7 P=0.7 P=0.7 处形成尖峰,当 n → ∞ n\\to\\infty n→∞,曲线形状逼近 δ ( x − 0.7 ) \\delta(x-0.7) δ(x−0.7)
实现代码如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
Pk = lambda k,n,p: comb(n,k)*(pk)*((1-p)(n-k))
p0 = 0.7
k20 = np.floor(20*p0).astype('int')
p20 = np.zeros(100)
k50 = np.floor(50*p0).astype('int')
p50 = np.zeros(100)
k100 = np.floor(100*p0).astype('int')
p100 = np.zeros(100)
i = np.arange(0,100)
p = i/100
P20 = Pk(k20,20,p)
P50 = Pk(k50,50,p)
P100 = Pk(k100,100,p)
y20m = max(P20)
y50m = max(P50)
y100m = max(P100)
plt.figure()
plt.plot(p[i],P20[i])
plt.plot(p[i],P50[i]*y20m/y50m)
plt.plot(p[i],P100[i]*y20m/y100m)
plt.legend(['n=20','n=50','n=100'],loc='upper left')
plt.show()
( 3 ) (3) (3) 当区域 R \\mathcal{R} R 足够小,可近似认为区域 R \\mathcal{R} R 中的概率密度是恒定的,若有一个样本 x ∈ R \\boldsymbol{x}\\in\\mathcal{R} x∈R,那么该样本落在区域 R \\mathcal{R} R 中的概率为
P = ∫ R p ( x ) d x ≈ p ( x ) V \\qquad\\qquad\\qquad P=\\displaystyle\\int_\\mathcal{R}p(\\boldsymbol{x})\\mathrm{d}\\boldsymbol{x} \\approx p(\\boldsymbol{x})V P=∫Rp(x)dx≈p(x)V 此处, V V V 为区域 R \\mathcal{R} R 的体积
\\qquad 此时,位于 x ∈ R \\boldsymbol{x}\\in\\mathcal{R} x∈R 处的概率密度值就可以表示为:
p ( x ) ≈ p ^ ( x ) = P V = k / n V \\qquad\\qquad\\qquad \\textcolor{crimson}{p(\\boldsymbol{x})\\approx}\\hat{p}(\\boldsymbol{x})=\\dfrac{P}{V}=\\textcolor{crimson}{\\dfrac{k/n}{V}} p(x)≈p^(x)=VP=Vk/n
\\qquad 因此, x \\boldsymbol{x} x 处的概率密度估计 p ^ ( x ) \\hat{p}(\\boldsymbol{x}) p^(x) 与样本数 n n n、包含 x \\boldsymbol{x} x 的区域 R \\mathcal{R} R、以及落入区域 R \\mathcal{R} R 中的样本数 k k k 有关。
\\qquad
● \\quad 考虑概率密度函数的估计 p ^ ( x ) = k / n V \\textcolor{crimson}{\\hat{p}(\\boldsymbol{x})=\\dfrac{k/n}{V}} p^(x)=Vk/n
( 1 ) (1) (1) 如果体积 V V V 的值是固定的,且能够获得足够多的样本,那么 P = k n P=\\frac{k}{n} P=nk 的值也可以足够精确(如图 1 1 1所示)。
\\qquad 此时, p ^ ( x ) = P V = ∫ R p ( x ) d x ∫ R d x \\hat{p}(\\boldsymbol{x})=\\dfrac{P}{V}=\\dfrac{\\displaystyle\\int_\\mathcal{R}p(\\boldsymbol{x})\\mathrm{d}\\boldsymbol{x}}{\\displaystyle\\int_\\mathcal{R}\\mathrm{d}\\boldsymbol{x}} p^(x)=VP=∫Rdx∫Rp(x)dx 是 p ( x ) p(\\boldsymbol{x}) p(x) 空间平均化的版本。
\\qquad 如果希望得到更精确的 p ( x ) p(\\boldsymbol{x}) p(x),而不是平滑后的版本,就必须要求体积 V → 0 V\\to0 V→0。
\\qquad
( 2 ) (2) (2) 另一方面,从取样的角度,能够获得的样本数总是有限的,体积 V V V 又不能任意小。
\\qquad 假设固定样本个数为 n n n,若体积 V V V 过小,在某处可能会:
\\qquad ① 体积 V V V 中不包含任何样本,导致此处的概率密度估计 p ^ ( x ) → 0 \\hat{p}(\\boldsymbol{x})\\to0 p^(x)→0;
\\qquad ② 体积 V V V 中只包含几个样本,导致此处的概率密度估计 p ^ ( x ) → ∞ \\hat{p}(\\boldsymbol{x})\\to\\infty p^(x)→∞。
\\qquad
\\qquad 因此,如果采用 p ^ ( x ) = k / n V \\textcolor{crimson}{\\hat{p}(\\boldsymbol{x})=\\dfrac{k/n}{V}} p^(x)=Vk/n 的方法来估计概率密度,那么 k n \\dfrac{k}{n} nk 的值总会有一定程度的变动,而概率密度估计 p ^ ( x ) \\hat{p}(\\boldsymbol{x}) p^(x) 总包含了一定程度的空间平滑。
\\qquad
( 3 ) (3) (3) 为了估计点 x \\boldsymbol{x} x 处的概率密度函数,采用如下方法:
\\qquad ① 构造一系列包含点 x \\boldsymbol{x} x 的区域: R 1 , R 2 , ⋯ \\mathcal{R}_1,\\mathcal{R}_2,\\cdots R1,R2,⋯,其中 R 1 \\mathcal{R}_1 R1 中包含了 1 1 1 个样本, R 2 \\mathcal{R}_2 R2 中包含了 2 2 2 个样本 ⋯ \\cdots ⋯;
\\qquad ② 记 V n V_n Vn 为区域 R n \\mathcal{R}_n Rn 的体积, k n k_n kn 为落在区域 R n \\mathcal{R}_n Rn 中的样本个数,用 p ^ n ( x ) \\hat{p}_n(\\boldsymbol{x}) p^n(x) 表示对概率密度 p ( x ) p(\\boldsymbol{x}) p(x) 的第 n n n 次估计。
\\qquad 那么 p ^ n ( x ) = k n / n V n \\textcolor{crimson}{\\hat{p}_n(\\boldsymbol{x})=\\dfrac{k_n/n}{V_n}} p^n(x)=Vnkn/n
\\qquad 如果要求 p ^ n ( x ) → p ( x ) \\hat{p}_n(\\boldsymbol{x})\\to p(\\boldsymbol{x}) p^n(x)→p(x),那么必须满足 { lim n → ∞ V n = 0 lim n → ∞ k n = ∞ lim n → ∞ k n n = 0 \\begin{cases}\\displaystyle\\lim_{n\\to\\infty}V_n=0\\\\\\displaystyle\\lim_{n\\to\\infty}k_n=\\infty\\\\\\displaystyle\\lim_{n\\to\\infty}\\textstyle \\frac{k_n}{n}=0\\end{cases} ⎩ ⎨ ⎧n→∞limVn=0n→∞limkn=∞n→∞limnkn=0
■ lim n → ∞ V n = 0 \\quad\\displaystyle\\lim_{n\\to\\infty}V_n=0 n→∞limVn=0 保证体积 V V V 能够尽可能小,从而减轻空间平滑的程度,使得 p ^ n ( x ) → p ( x ) \\hat{p}_n(\\boldsymbol{x})\\to p(\\boldsymbol{x}) p^n(x)→p(x);
■ lim n → ∞ k n = ∞ \\quad\\displaystyle\\lim_{n\\to\\infty}k_n=\\infty n→∞limkn=∞ 保证在 V V V 尽可能小的情形下仍包含了大量样本,如果在点 x \\boldsymbol{x} x 处的 p ^ ( x ) ≠ 0 \\hat{p}(\\boldsymbol{x})\\neq0 p^(x)=0,那么 k n n → P \\frac{k_n}{n}\\to P nkn→P(如图 1 1 1所示);
■ lim n → ∞ k n n = 0 \\quad\\displaystyle\\lim_{n\\to\\infty}\\textstyle\\frac{k_n}{n}=0 n→∞limnkn=0 保证在 V V V 尽可能小的情形下,尽管包含了大量的样本 k n ( k n → ∞ ) k_n\\ (k_n\\to\\infty) kn (kn→∞),但相对于样本总数 n ( n → ∞ ) n\\ (n\\to\\infty) n (n→∞) 来说,还是可以忽略的 ( k n n → 0 ) (\\dfrac{k_n}{n}\\to0) (nkn→0),进而保证了 lim n → ∞ k n / n V n \\displaystyle\\lim_{n\\to\\infty}\\dfrac{k_n/n}{V_n} n→∞limVnkn/n 的收敛性。
1. Parzen窗方法
\\qquad 根据某一个确定的体积函数来逐渐收缩到一个给定的区间,就是 Parzen \\text{Parzen} Parzen窗方法。
● Parzen \\quad\\text{Parzen} Parzen窗方法估计概率密度函数的基本思路
( 1 ) \\qquad(1) (1) 考虑 d d d 维空间,令 h n h_n hn 表示超立方体的边长,该超立方体的体积为 h n d h_n^d hnd
( 2 ) \\qquad(2) (2) 定义窗函数 φ ( u ) = { 1 , ∣ u j ∣ ≤ 1 2 0 , ∣ u j ∣ > 1 2 , j = 1 , 2 , ⋯ , d \\varphi(\\boldsymbol{u})=\\begin{cases}1&,\\vert u_j\\vert\\le\\frac{1}{2} \\\\ 0&,\\vert u_j\\vert>\\frac{1}{2}\\end{cases},\\quad j=1,2,\\cdots,d φ(u)={10,∣uj∣≤21,∣uj∣>21,j=1,2,⋯,d
\\qquad 显然, φ ( u ) \\varphi(\\boldsymbol{u}) φ(u) 表示一个中心在原点、边长为 1 1 1 的立方体
\\qquad 如果点 x i \\boldsymbol{x}_i xi 包含在以点 x \\boldsymbol{x} x 为中心的单位超立方体中,必然有 φ ( x − x i h n ) = 1 \\varphi\\left(\\dfrac{\\boldsymbol{x}-\\boldsymbol{x}_i}{h_n}\\right)=1 φ(hnx−xi)=1
( 3 ) \\qquad(3) (3) 因此,以点 x \\boldsymbol{x} x 为中心的超立方体中包含的样本点数为:
k n = ∑ i = 1 n φ ( x − x i h n ) \\qquad\\qquad\\qquad k_n=\\displaystyle\\sum_{i=1}^n\\varphi\\left(\\dfrac{\\boldsymbol{x}-\\boldsymbol{x}_i}{h_n}\\right) kn=i=1∑nφ(hnx−xi)
\\qquad 那么由 p ^ n ( x ) = k n / n V n \\textcolor{mediumblue}{\\hat{p}_n(\\boldsymbol{x})=\\dfrac{k_n/n}{V_n}} p^n(x)=Vnkn/n,可得到 Parzen \\text{Parzen} Parzen 窗法的概率密度估计为:
p ^ n ( x ) = 1 n ∑ i = 1 n 1 V n φ ( x − x i h n ) , V n = h n d \\qquad\\qquad\\qquad\\textcolor{crimson}{\\hat{p}_n(\\boldsymbol{x})=\\dfrac{1}{n}\\displaystyle\\sum_{i=1}^n\\dfrac{1}{V_n}\\varphi\\left(\\dfrac{\\boldsymbol{x}-\\boldsymbol{x}_i}{h_n}\\right)}\\ ,\\quad V_n=h_n^d p^n(x)=n1i=1∑nVn1φ(hnx−xi) ,Vn=hnd
\\qquad 从 p ^ n ( x ) \\hat{p}_n(\\boldsymbol{x}) p^n(x) 的形式上可以看出,其本质上是一个基于核函数的内插公式。同时,也说明了概率密度函数估计可以采用更一般的方式,而不必规定窗函数必须是超立方体。
\\quad
● \\quad 窗宽 h n h_n hn 对 p ^ n ( x ) \\hat{p}_n(\\boldsymbol{x}) p^n(x) 的影响
\\qquad 定义函数 ϕ n ( x ) = 1 V n φ ( x h n ) \\textcolor{blue}{\\phi_n(\\boldsymbol{x})=\\dfrac{1}{V_n}\\varphi\\left(\\dfrac{\\boldsymbol{x}}{h_n}\\right)} ϕn(x)=Vn1φ(hnx),那么 Parzen \\text{Parzen} Parzen 窗法的概率密度估计为:
p ^ n ( x ) = 1 n ∑ i = 1 n ϕ n ( x − x i ) \\qquad\\qquad\\qquad\\textcolor{crimson}{\\hat{p}_n(\\boldsymbol{x})=\\dfrac{1}{n}\\displaystyle\\sum_{i=1}^n\\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i)} p^n(x)=n1i=1∑nϕn(x−xi)
( 1 ) \\qquad(1) (1) 如果 h n h_n hn 很大,则 ϕ n ( x − x i ) \\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i) ϕn(x−xi) 的强度非常低,即使 x i \\boldsymbol{x}_i xi 远离 x \\boldsymbol{x} x, ϕ n ( x − x i ) \\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i) ϕn(x−xi) 与 ϕ n ( 0 ) \\phi_n(0) ϕn(0) 相差不太大。
( 2 ) \\qquad(2) (2) 如果 h n h_n hn 很小,则 ϕ n ( x − x i ) \\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i) ϕn(x−xi) 的强度非常高,只有离 x \\boldsymbol{x} x 非常近的 x i \\boldsymbol{x}_i xi 才对计算 ϕ n ( x − x i ) \\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i) ϕn(x−xi) 有贡献,即: h n h_n hn 越小, ϕ n ( x − x i ) \\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i) ϕn(x−xi) 越尖。
当 h n → 0 h_n\\to0 hn→0, ϕ n ( x − x i ) \\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i) ϕn(x−xi) 逼近狄拉克函数 δ ( x − x i ) \\delta(\\boldsymbol{x}-\\boldsymbol{x}_i) δ(x−xi) ,此时的概率密度估计为 p ^ n ( x ) = 1 n ∑ i = 1 n δ ( x − x i ) \\textcolor{crimson}{\\hat{p}_n(\\boldsymbol{x})=\\dfrac{1}{n}\\displaystyle\\sum_{i=1}^n\\delta(\\boldsymbol{x}-\\boldsymbol{x}_i)} p^n(x)=n1i=1∑nδ(x−xi)。
\\qquad 对于任意窗宽 h n h_n hn,其概率分布满足归一性:
∫ ϕ n ( x − x i ) d x = ∫ 1 V n φ ( x − x i h n ) d x = ∫ φ ( u ) d u = 1 \\qquad\\qquad\\qquad\\displaystyle\\int\\phi_n(\\boldsymbol{x}-\\boldsymbol{x}_i)\\mathrm{d}\\boldsymbol{x}=\\int\\dfrac{1}{V_n}\\varphi\\left(\\dfrac{\\boldsymbol{x}-\\boldsymbol{x}_i}{h_n}\\right)\\mathrm{d}\\boldsymbol{x}=\\int\\varphi\\left(\\boldsymbol{u}\\right)\\mathrm{d}\\boldsymbol{u}=1 ∫ϕn(x−xi)dx=∫Vn1φ(hnx−xi)dx=∫φ(u)du=1
\\qquad 因此,窗宽的选择对概率密度估计 p ^ n ( x ) \\hat{p}_n(\\boldsymbol{x}) p^n(x) 的影响非常大,如下例所示。
\\qquad
《模式分类》图4.5实现代码(假设真实概率密度为标准正态分布)
高斯窗函数: φ ( u ) = 1 2 π e − u 2 2 \\varphi(u)=\\dfrac{1}{2\\pi}e^{-\\frac{u^2}{2}} φ(u)=2π1e−2u2
概率密度估计: p ^ n ( x ) = 1 n ∑ i = 1 n 1 h n φ ( x − x i h n ) \\hat{p}_n(x)=\\dfrac{1}{n}\\displaystyle\\sum_{i=1}^n\\dfrac{1}{h_n}\\varphi\\left(\\dfrac{x-x_i}{h_n}\\right) p^n(x)=n1i=1∑nhn1φ(hnx−xi)
import numpy as np
import matplotlib.pyplot as plt
def parzen1d(sample, x, h):kernel = lambda u: np.exp(-u2/2)/np.sqrt(2*np.pi)pdf = np.zeros(len(x))for i in range(len(sample)):pdf += kernel((x-sample[i])/h)/h return pdf/len(sample)
def parzen1d_show(num):x = np.linspace(-3, 3, 100) rx = np.random.randn(num)ry = np.zeros_like(rx) pdf1 = parzen1d(rx, x, 1.0)pdf2 = parzen1d(rx, x, 0.5)pdf3 = parzen1d(rx, x, 0.1) plt.figure(figsize=(12,2))plt.subplot(131),plt.plot(rx, ry, 'r.', markersize='3'),plt.plot(x,pdf1),plt.title('h=1')plt.xticks([-3,-2,-1,0,1,2,3])plt.subplot(132),plt.plot(rx, ry, 'r.', markersize='3'),plt.plot(x,pdf2),plt.title('h=0.5')plt.xticks([-3,-2,-1,0,1,2,3])plt.subplot(133),plt.plot(rx, ry, 'r.', markersize='3'),plt.plot(x,pdf3),plt.title('h=0.1')plt.xticks([-3,-2,-1,0,1,2,3]) plt.show()
parzen1d_show(1)
parzen1d_show(10)
parzen1d_show(100)
parzen1d_show(10000)
采用高斯窗函数时的结果:
\\qquad 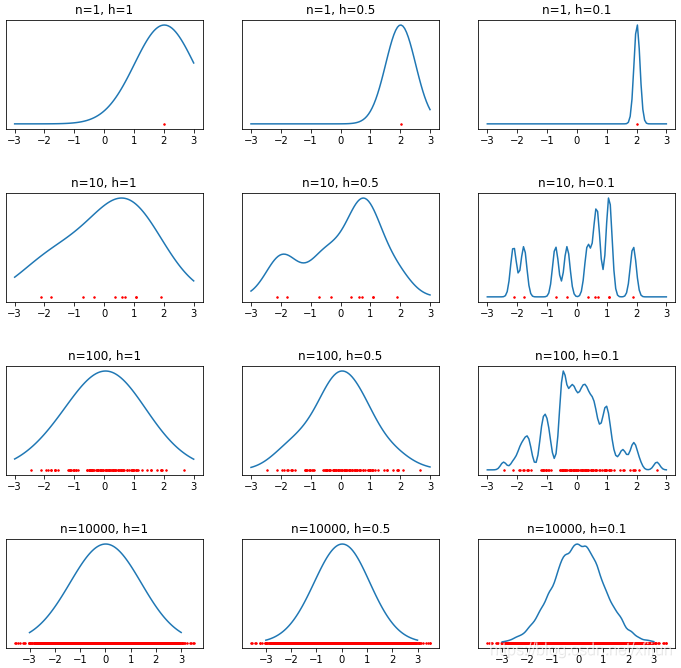
采用矩形窗时的结果:
\\qquad 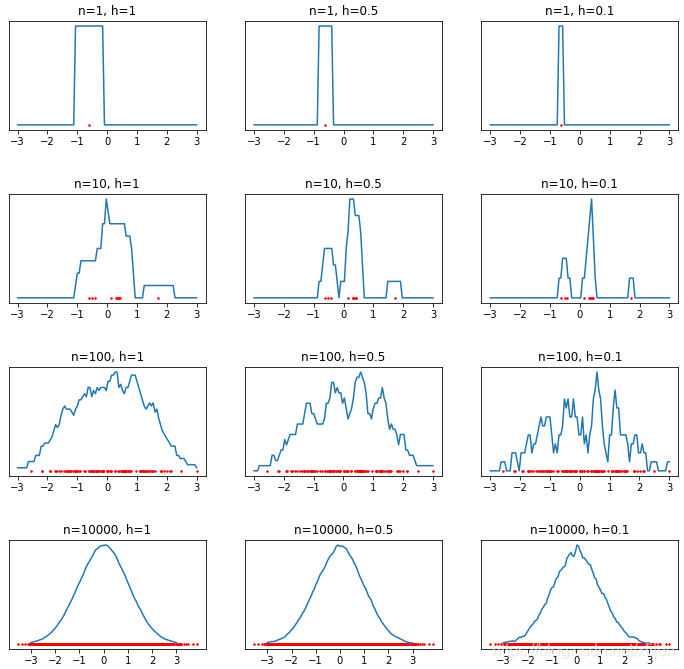
二维 Parzen \\text{Parzen} Parzen窗概率密度估计:
\\qquad 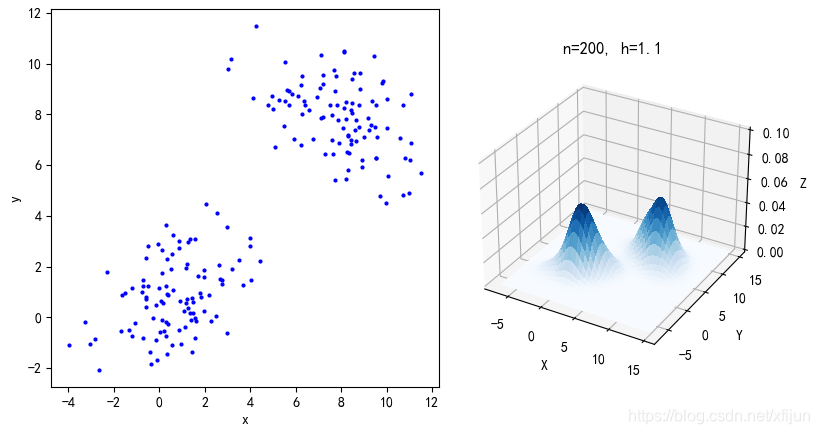
2. kn近邻估计
k n \\qquad k_n kn 近邻估计,是另一种非参数的概率密度函数估计方法,其基本思路是让体积成为训练样本数 n n n 的函数。
\\qquad 为了估计点 x \\boldsymbol{x} x 处的概率密度,以点 x \\boldsymbol{x} x 为中心不断扩张体积,直到体积 V n V_n Vn 内包含了 k n k_n kn 个相邻的样本点(其中, k n k_n kn 是训练样本数 n n n 的函数),则点 x \\boldsymbol{x} x 处的概率密度估计为:
p ^ n ( x ) = k n / n V n \\qquad\\qquad\\qquad\\hat{p}_n(\\boldsymbol{x})=\\dfrac{k_n/n}{V_n} p^n(x)=Vnkn/n
( 1 ) \\qquad(1) (1) 如果点 x \\boldsymbol{x} x 处的概率密度比较小,包含 k n k_n kn 个相邻点的体积就相对比较大;
( 2 ) \\qquad(2) (2) 如果点 x \\boldsymbol{x} x 处的概率密度比较大,包含 k n k_n kn 个相邻点的体积就相对比较小;如果点 x \\boldsymbol{x} x 处的概率密度非常高,随着 V n → 0 V_n\\to0 Vn→0,体积的生长就会停止。
在 Parzen \\text{Parzen} Parzen 窗方法中,体积是训练样本数 n n n 某个固定的形式
在 k n k_n kn- 最近邻方法中,体积必须能够包含 k n k_n kn 个相邻样本点
\\qquad
《模式分类》图4.12实现代码:(假设真实概率密度为标准正态分布)
k n = n , V n = 2 ∗ sort ( d i s t ) [ k n ] k_n=\\sqrt{n},\\ V_n=2*\\text{sort}(dist)[k_n] kn=n, Vn=2∗sort(dist)[kn]
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def knn_pdf(sample, x):num = len(sample)pdf = np.zeros(len(x))kn = num(0.5)for i in range(len(x)):dist = np.abs(x[i] - sample)sortedDist = np.sort(dist) vol = sortedDist[int(kn)-1]*2pdf[i] = kn/num/volreturn pdf
def knn1d(num):mean = 0std = 1x = np.linspace(-4, 4, 1000) y = norm.pdf(x, mean, std)rx = mean + std * np.random.randn(num)ry = np.zeros_like(rx) pdf = knn_pdf(rx, x)plt.figure(figsize=(5,4))plt.plot(x,y,'r')plt.plot(rx, ry, 'r.', markersize='3')plt.plot(x,pdf,'g');plt.title('n={}'.format(num))plt.xticks([-4,-3,-2,-1,0,1,2,3,4]),plt.yticks([])
knn1d(1)
knn1d(16)
knn1d(256)
knn1d(4096)
plt.show()
运行结果:
\\qquad 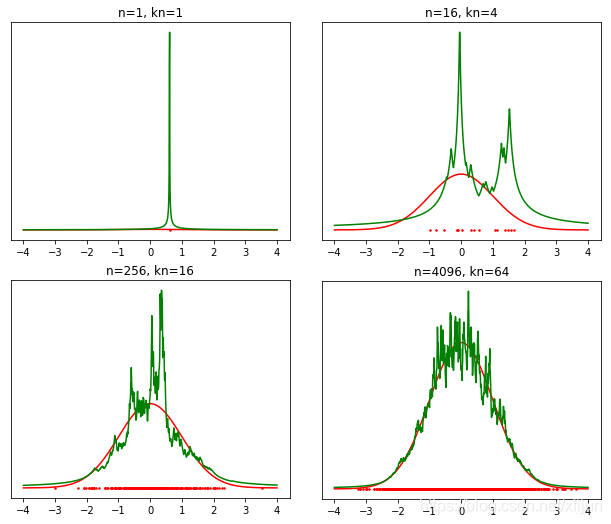
当 n → ∞ n\\to\\infty n→∞ 时, k n k_n kn 近邻估计需采用 k d kd kd 树这样的快速搜索算法,可以考虑用核回归方法把概率密度估计对 k n k_n kn 近邻估计的结果进行平滑,似乎此时的窗宽相对容易选择一些。
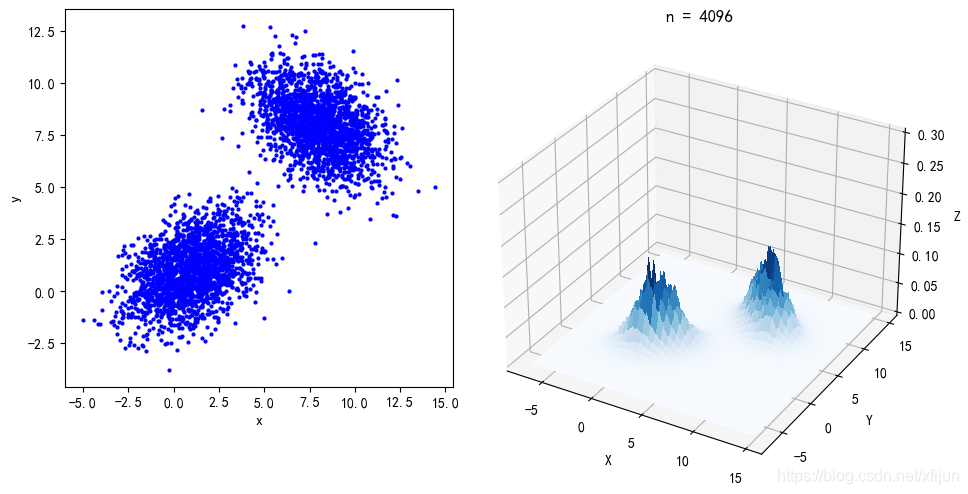
二维 k n k_n kn近邻概率密度估计
def knn2d(num):mu = [1,1]cov = [[3,1],[1,2]]sample1 = np.random.multivariate_normal(mu,cov,num//2)mu = [8,8]cov = [[3,-1],[-1,2]]sample2 = np.random.multivariate_normal(mu,cov,num//2)sample = np.concatenate((sample1, sample2))plt.figure(figsize=(5,5))plt.plot(sample[:,0], sample[:,1],'b.',markersize='4')plt.xlabel('x'), plt.ylabel('y') fig = plt.figure(figsize=(8,6))ax = fig.add_subplot(projection='3d')X = np.arange(-7, 15, 0.1)Y = np.arange(-7, 15, 0.1)x, y = np.meshgrid(X, Y)pos = np.empty(x.shape + (2,))pos[:, :, 0] = xpos[:, :, 1] = yx1 = x.reshape(-1,1)y1 = y.reshape(-1,1)xy = np.concatenate((x1, y1), axis=1)pdf = np.zeros(x.shape)h,w = x.shapekn = int(num(0.5))for i in range(len(xy)):dist = np.sqrt(np.sum((sample - xy[i,:])2,axis=1))sortedDist = np.sort(dist) vol = sortedDist[kn-1]2i0 = i//hj0 = i % wpdf[i0,j0] = kn/num/volsurf = ax.plot_surface(x, y, pdf, cmap=cm.Blues, linewidth=1, antialiased=False)ax.view_init(elev=30., azim=300)ax.set_zlim(0, 0.3)plt.title('n = {}'.format(num))
运行结果:
\\qquad 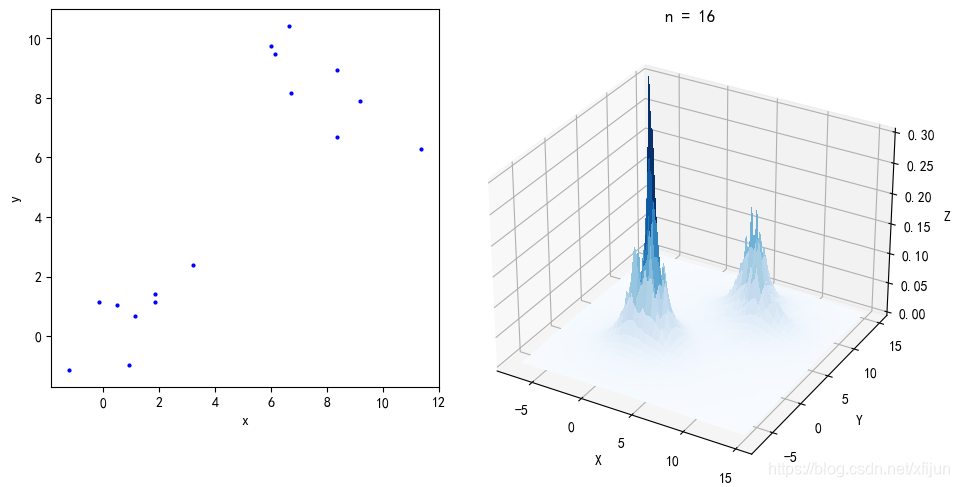
\\qquad