> 文章列表 > 「数字信号处理」MATLAB设计双音多频拨号系统

「数字信号处理」MATLAB设计双音多频拨号系统

文章列表

「数字信号处理」MATLAB设计双音多频拨号系统

前言

实验目的：用Matlab模拟实现双音多频拨号系统

输入：一串数字模拟电话号码

输出：检测出的电话号码

Matlab版本：2021b

系统：MacOS

实验方法：查表法+戈泽尔函数

实验大意

任意一个数字可以表示为两个余弦信号的相加，因此我们这里将接收到的电话号码首先需要转化为这样的时域序列。转化规则如下

将时域序列x[n]作为goertzel函数的输入，返回值是该离散时域序列对应的离散傅里叶变换。

从表格中可以看出，我们共有8种频率，因此我们定义数组k为当采样点个数N=205个时，每个频率对应于第几个采样点。我们检测这8个采样点，观察他们的幅度，幅度最大的两个采样点对应的频率即为当前输入的数字对应表格中的频率。这样，我们就能检测出当前接收到的数字是几。由于电话信号的典型采样频率为8kHz，这里Ts(抽样周期)就为 1/8000s。

两个关键问题：

为什么选择8000Hz作为采样频率，为什么这个采样频率可行

为什么采样点个数为205

1. 要检测的信号频率范围是697 ~ 1633Hz，但考虑到存在语音干扰，除了检测这8个频率外，还要检测它们的二次倍频的幅度大小，波形正常且干扰小的正弦波的二次倍频是很小的，如果发现二次谐波很大，则不能确定这是DTMF信号。这样频谱分析的频率范围为697 ~ 3266Hz。按照采样定理，采样频率应该大于2倍的最大频率，即6532Hz。因此这里选择8000Hz作为采样频率，符合要求。

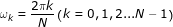
2. DFT的采样频率为 $\\small \\omega _{k}=\\frac{2\\pi k}{N}\\left ( k=0,1,2...N-1 \\right )$

相应的模拟域的采样点频率为 $\\small f_{k}=\\frac{F_{s} k}{N}\\left ( k=0,1,2...N-1 \\right )$

我们希望选择一个合适的N，使用该公式算出的 $\\small f_{k}$ 能接近要检测的频率，或者用8个频率中的任一个频率代入公式中时，得到的k值最接近整数值，这样虽然用幅度最大点检测的频率有误差，但仍可以准确判断所对应的DTMF频率，进而准确判断所对应的数字或者符号。经过不同数值N的测试后得出结论，N=205时，结果最好。

MATLAB实现代码

% Low Frequency 
f1 = 697;
f2 = 770;
f3 = 852;
f4 = 941;
% High Frequency 
F1 = 1209;
F2 = 1336;
F3 = 1477;
F4 = 1633;N = 205; % The quantity of sampling points 
Fs = 8000; % Sampling Frequency 
T = 1/Fs; % Sampling Period 
t = [0:N-1]*T; % t = n*T% The table for look up 
k1 = cos(2*pi*f1*t) + cos(2*pi*F1*t);
k2 = cos(2*pi*f1*t) + cos(2*pi*F2*t);
k3 = cos(2*pi*f1*t) + cos(2*pi*F3*t);
ka = cos(2*pi*f1*t) + cos(2*pi*F4*t);
k4 = cos(2*pi*f2*t) + cos(2*pi*F1*t);
k5 = cos(2*pi*f2*t) + cos(2*pi*F2*t);
k6 = cos(2*pi*f2*t) + cos(2*pi*F3*t);
kb = cos(2*pi*f2*t) + cos(2*pi*F4*t);
k7 = cos(2*pi*f3*t) + cos(2*pi*F1*t);
k8 = cos(2*pi*f3*t) + cos(2*pi*F2*t);
k9 = cos(2*pi*f3*t) + cos(2*pi*F3*t);
kc = cos(2*pi*f3*t) + cos(2*pi*F4*t);
km = cos(2*pi*f4*t) + cos(2*pi*F1*t); % *
k0 = cos(2*pi*f4*t) + cos(2*pi*F2*t);
kj = cos(2*pi*f4*t) + cos(2*pi*F3*t); % # 
kd = cos(2*pi*f4*t) + cos(2*pi*F4*t);% 4*4 matrix monitoring the table
key=['1','2','3','a';'4','5','6','b';'7','8','9','c';'*','0','#','d']; k=[18,20,22,24,31,34,38,42]; % the points corrsponding 8 frequencies %-----------------------pre process----------------------------------------num = input('please enter the key:','s'); % input as a string 
num = num - '0'; % minus the offset (ascii)
len = length(num); % the length of the input telephone number 
disp('The number of the key is: ');
disp(len); % display the length 
number = zeros(len, length(t)); % len * length(t) zero matrix for i = 1:len % for every number in input switch num(i) % Look-up table methodcase 1number(i,1:N) = k1;case 2  number(i,1:N) = k2;case 3  number(i,1:N) = k3;case 4  number(i,1:N) = k4;case 5  number(i,1:N) = k5;case 6  number(i,1:N) = k6;case 7  number(i,1:N) = k7;case 8  number(i,1:N) = k8;case 9  number(i,1:N) = k9;case 0  number(i,1:N) = k0;case 49  number(i,1:N) = ka;case 50  number(i,1:N) = kb;case 51  number(i,1:N) = kc;case 52  number(i,1:N) = kd;case -6  % number is *number(i,1:N) = km;case -13 % number is #number(i,1:N) = kj;otherwiseerror('The key is not right!');end
enddisp('The key is: ');
for i = 1:lendft = goertzel(number(i,1:N), k+1); % return Discrete Fourier Transformfigure;x = [697, 770, 852, 941, 1209, 1336, 1477, 1633]; % The 8 frequency magnitude stem(x, abs(dft), '.');xlabel('Hz');title('Frequency Spectrum');idx = find(abs(dft) > 50); % find the frequency where dft is not zero disp(key(idx(1), idx(2) - 4));
end