微分学与梯度下降法

文章列表

微分学与梯度下降法

1.微分学的基本思想和方法

1.1 微分学的核心思想：函数逼近

微分学的核心思想是用熟悉且简单的函数对复杂函数进行局部逼近。

常用作逼近的简单函数包括：

线性函数：函数的一阶导数
多项式函数：泰勒级数

1.2 微积分的基础语言：极限论

极限的表达方式：

自然语言：当 $x$ 趋向于 $a$ 时， $f (x)$ 的极限是 $L$ 。
数学符号：
$lim⁡x→af(x)=L\\lim\\limits_{x \\to a}f(x)=L$
标准语言：对于任意的 $ϵ>0\\epsilon \\gt 0$ ,存在一个 $δ>0\\delta \\gt 0$ ，对于任意的 $\\in\\ (a+\\delta ,a+\\delta )$ ，均有 $∣f(x)−L∣<ϵ\\vert f(x)-L\\vert \\lt \\epsilon$ 。
无穷小：一般把趋于零的极限成为无穷小。
无穷小阶数：趋于零的速度越快的无穷小，其阶数越高。比如： $xn,x→0x^n,x \\to\\ 0$ 趋于零的速度还快的无穷小记为 $o(x^n)$ 。
两边夹定理：如果 $\\lt g(x) \\lt h(x)$ ，而且这三个函数都在 $a$ 处有极限，那么则有：
$lim⁡x→af(x)≤lim⁡x→ag(x)≤lim⁡x→ah(x)\\lim \\limits_{x\\to\\ a}f(x) \\le \\lim \\limits_{x\\to\\ a}g(x) \\le \\lim \\limits_{x\\to\\ a}h(x)$
重要极限(两边夹定理应用)：
- 三角函数
  $lim⁡x→0sin⁡(x)x=1\\lim \\limits_{x \\to\\ 0} \\frac{\\sin(x)}{x} =1$
- 自然对数底数
  $lim⁡n→∞(1+1n)n=e\\lim \\limits_{n \\to\\ \\infty}\\left(1+\\frac{1}{n}\\right)^n =e$
- 指数函数
  $lim⁡x→0ex−1x=1\\lim \\limits_{x \\to\\ 0} \\frac{e^x-1}{x} =1$

1.3 微分学的基本手法：求导数

微分学的核心思想就是逼近。

一阶导数：
$f´(x)=lim⁡Δ→0f(Δx+x)−f(x)Δxf^´(x)=\\lim \\limits_{\\Delta \\to\\ 0}\\frac{f(\\Delta x+x)-f(x)}{\\Delta x}$

几何意义：用直线逼近曲线
代数意义：用线性函数逼近复杂函数

对函数进行线性逼近：

假设函数 $f (x)$ 是一个可微函数， $x_0$ 是定义域中的一个点，那么则有：
$f(x0+Δx)=f(x0)+Δ⋅df(x0)dx+o(Δ)f(x_0+\\Delta x)=f(x_0)+\\Delta ·\\frac{df(x_0)}{dx}+o(\\Delta)$
注：现在数学符号常用如下记号：
$dx=Δdf(x0)=f(x0+Δx)−f(x0)+o(Δ)dx=\\Delta \\\\[2ex] df(x_0)=f(x_0+\\Delta x)-f(x_0)+o(\\Delta)$
故上面的微分公式可以写成：
$df(x0)=f(x0)dx⋅dxdf(x_0)=\\frac{f(x_0)}{dx}·dx$
常见函数的导数：

多项式函数:
$dxndx=n⋅xn−1\\frac{dx^n}{dx}=n·x^{n-1}$
三角函数:
$dsin⁡(x)dx=cos⁡(x)\\frac{d\\sin(x)}{dx}=\\cos(x)$
指数函数:
$dexdx=ex\\frac{de^x}{dx}=e^x$

1.4 从线性逼近到多项式逼近：泰勒级数

一元微分学的顶峰：Taylor级数(对函数进行高阶逼近)

导数的导数就是二阶导数
$n$ 阶导数的导数就是 $n + 1$ 阶导数
Taylor级数就是利用 $n$ 阶导数来对函数进行高阶逼近

Taylor级数(对函数进行高阶逼近)

如果一个函数 $f (x)$ 是 $n$ 阶可微函数，那么则有：
$f(x0+Δx)=f(x0)+f(1)(x0)⋅Δx+12f(2)(x)⋅Δx2+...+1n!f(n)(x0)Δxn+o(Δxn)f(x_0+\\Delta x)=f(x_0)+f^{(1)}(x_0)·\\Delta x+\\frac{1}{2}f^{(2)}(x)·\\Delta x^2+...+\\frac{1}{n!}f^{(n)}(x_0)\\Delta x^n+o(\\Delta x^n)$
函数 $f (x)$ 的 $n$ 阶Taylor级数就是与 $f (x)$ 拥有相同前 $n$ 阶导数的 $n$ 阶多项式。

当 $n = 2$ 时，Taylor级数就成为一个二次逼近：

对于2阶可微函数 $f (x)$ :
$f(x0+Δx)=f(x0)+f(1)(x0)⋅Δx+12f(2)(x)⋅Δx2+o(Δx2)f(x_0+\\Delta x)=f(x_0)+f^{(1)}(x_0)·\\Delta x+\\frac{1}{2}f^{(2)}(x)·\\Delta x^2+o(\\Delta x^2)$
而这构成了牛顿法的基础。

1.5 从低维到高维：多元函数的梯度

对于一个二元函数 $f (x, y)$ ,偏导数定义为：
$∂xf(x,y)=∂∂xf(x,y)=lim⁡Δx→0f(x+Δx,y)−f(x,y)Δx∂yf(x,y)=∂∂yf(x,y)=lim⁡Δy→0f(x+Δy,y)−f(x,y)Δy\\partial_xf(x,y)=\\frac{\\partial}{\\partial x}f(x,y)=\\lim\\limits_{\\Delta_x \\to\\ 0}\\frac{f(x+\\Delta_x,y)-f(x,y)}{\\Delta_x} \\\\[3ex] \\partial_yf(x,y)=\\frac{\\partial}{\\partial y}f(x,y)=\\lim\\limits_{\\Delta_y \\to\\ 0}\\frac{f(x+\\Delta_y,y)-f(x,y)}{\\Delta_y}$
沿着方向 $v = (a, b)$ 的方向导数为：
$∇vf(x,y)=lim⁡Δ→0f(x+Δ⋅a,y+Δ⋅b)−f(x,y)Δ\\nabla_vf(x,y)=\\lim\\limits_{\\Delta \\to\\ 0}\\frac{f(x+\\Delta·a,y+\\Delta·b)-f(x,y)}{\\Delta}$
偏导数：沿着坐标轴方向的方向导数。

多元可微函数，一个二元函数 $f (x, y)$ 一阶可微，如果存在 $L_x,L_y$ 使得：
$f(x+Δx,y+Δy)=f(x,y)+Lx⋅Δx+Ly⋅Δy+o(∣Δx∣+∣Δy∣)f(x+\\Delta x,y+\\Delta y)=f(x,y)+L_x·\\Delta_x+L_y·\\Delta_y+o(\\vert\\Delta_x\\vert+\\vert\\Delta_y\\vert)$
梯度(以二元函数为例)

对于可微函数 $f (x, y)$ ，梯度的定义为：
$∇f(x,y)=(∂xf,∂yf)T\\nabla f(x,y)=(\\partial_xf,\\partial_yf)^T$
梯度的代数意义：其任意方向的偏导数可以由梯度来表示，如果 $v = (a, b)$ ，则有：
$∇vf(x,y)=v⋅∇f(x,y)=a∂xf(x,y)+b∂yf(x,y)\\nabla_v f(x,y)=v·\\nabla f(x,y)=a\\partial_xf(x,y)+b\\partial_yf(x,y)$
梯度的几何意义：梯度方向是函数增长最快的方向

2.梯度下降法和牛顿法

2.1 梯度下降法

如果 $J(θ)J(\\theta)$ 是一个多元函数，在 $θ0\\theta_0$ 点附近对于 $J(θ)J(\\theta)$ 做线性逼近:
$J(θ0+Δθ)=J(θ0)+ΔθT⋅∇J(θ0)+o(∣Δθ∣)J(\\theta_0+\\Delta_\\theta)=J(\\theta_0)+\\Delta^T_\\theta·\\nabla J(\\theta_0)+o(\\vert\\Delta_\\theta\\vert)$
上述线性逼近不能告诉我们极值点在上面地方，只能告诉我们极值点在什么方向。所以只能选取一个比较”小“的学习率 $η\\eta$ 来沿着这个方向走下去，并且得到梯度下降法的序列：
$θn=θn−1−ηn−1∇J(θn−1)\\theta_n=\\theta_{n-1}-\\eta_{n-1}\\nabla J(\\theta_{n-1})$
梯度下降法：对函数进行一阶逼近寻找函数下降最快的方向。 如同人下山一样，直至获得一个局部或者全局(损失函数是凸函数)最小值。
微分学与梯度下降法

牛顿法：对函数进行二阶逼近，并且直接估计函数的极小值点。
$f(θ0+Δθ)=f(θ0)+ΔθT⋅∇f(θ0)+12ΔθTHf(θ0)Δθ+o(∣Δθ∣2)f(\\theta_0+\\Delta_\\theta)=f(\\theta_0)+\\Delta^T_\\theta·\\nabla f(\\theta_0)+\\frac{1}{2}\\Delta^T_\\theta H f(\\theta_0)\\Delta_\\theta+o(\\vert\\Delta_\\theta\\vert^2)$
于是关于 $Δθ\\Delta_\\theta$ 的梯度为：
$ΔθT⋅∇f(θ0)+Hf(θ0)Δθ+o(∣Δθ∣)\\Delta^T_\\theta·\\nabla f(\\theta_0)+H f(\\theta_0)\\Delta_\\theta+o(\\vert\\Delta_\\theta\\vert^)$
零点近似值为：
$Δθ=Hf(θ0)−1⋅∇f(θ)\\Delta_\\theta=Hf(\\theta_0)^{-1}·\\nabla f(\\theta)$

难点

梯度计算

在机器学习和统计参数估计问题中目标函数经常是求和函数的形式：
$Jx(θ)=∑iJxi(θ)\\begin{align} &J_x(\\theta)=\\sum\\limits_iJ_{x_i}(\\theta) \\\\[2ex] \\end{align}$
其中每一个函数 $Jxi(θ)J_{x_i}(\\theta)$ 都对应一个样本 $x_i$ 。当样本量极大时，梯度的计算就会变得非常耗时耗力。
学习率选择

学习率选择过小会导致算法收敛很慢，学习率选择过大容易导致算法不收敛。

Q：为何沿着梯度负方向就是最速下降，即函数下降的速度最快？

在某个要优化的函数 $f (x)$ ，在x点处沿方向 $v$ 进行移动，到达 $f (x + v)$ ，图示表示了移动过程：

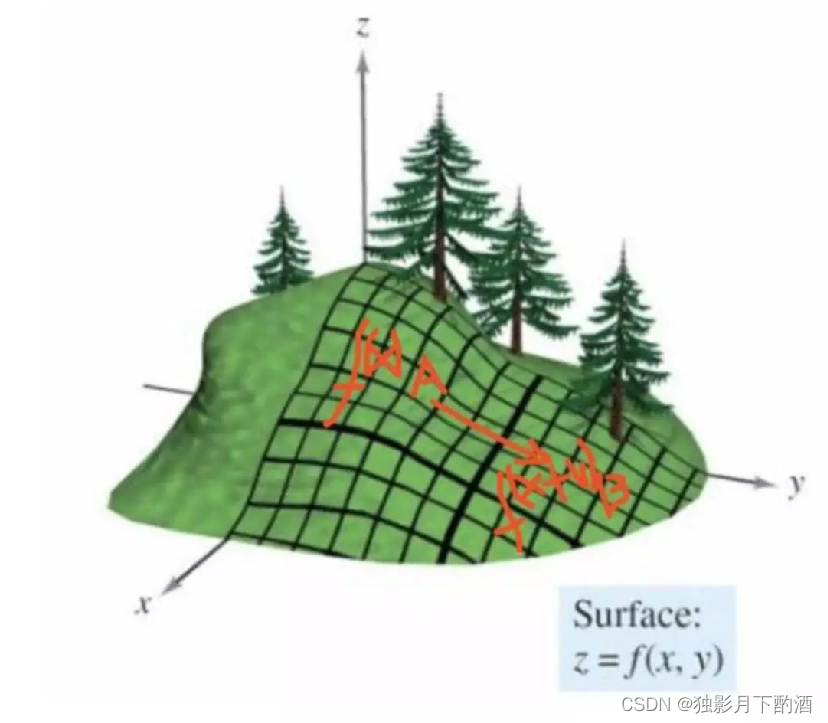
微分学与梯度下降法

上图显示了从A点,移动到B点的过程。那么 $v$ 方向是什么的时候，局部下降的最快呢？

换成数学语言来说就是， $f (x + v) - f (x)$ 的值在 $v$ 是什么的时候，达到最大！

对 $f (x + v)$ 在 $x$ 处进行Taylor一阶展开有：
$\\approx f(x)+\\nabla f(x)^Tv \\\\[2ex] f(x)-f(x+v) \\approx-\\nabla f(x)^Tv$
则 $f (x + v) - f (x) = df (x) v$ ，可以得出： $df (x) v$ 为函数值的变化量，注意的是 $df (x)$ 和 $v$ 均为向量， $df (x) v$ 也就是两个向量进行点积，而向量进行点积的最大值，也就是两者共线的时候，也就是说 $v$ 的方向和 $df (x)$ 方向相同的时候，点积值最大，这个点积值也代表了从A点到B点的上升量。而 $df (x)$ 正是代表函数值在 $x$ 处的梯度。所以梯度方向是函数局部上升最快的方向，也就证明了梯度的负方向是局部下降最快的方向。

2.2 随机梯度下降法

随机梯度下降法主要是为了解决第一个问题：梯度计算。

梯度下降法分为三种类型：

批量梯度下降法(BGD- batch gradient descent )

需要在整个数据集上计算所有的梯度，所以批梯度下降法的速度会很慢，同时，批梯度下降法无法处理超出内存容量限制的数据集。批梯度下降法同样也不能在线更新模型，即在运行的过程中，不能增加新的样本。

# 批梯度下降法
for i in range(nb_epochs):params_grad = evaluate_gradient(loss_function, data, params)params = params - learning_rate * params_grad

随机梯度下降法(SGD- stochastic gradient descent)

每次梯度计算只使用一个样本
- 避免在类似样本计算梯度造成冗余值
- 增加跳出当前的局部最小值的潜力
- 在逐渐缩小学习率的情况下，有与批梯度下降法类似的收敛速度

#随机梯度下降法
for i in range(nb_epochs):np.random.shuffle(data)for example in data:params_grad = evaluate_gradient(loss_function, example, params)params = params - learning_rate * params_grad

小批量随机梯度下降法(mini batch SGD)

每次梯度计算使用一个小批量样本
- 梯度计算比单样本更加稳定
- 可以很好利用现成的高度优化的矩阵运算工具

# 小批量随机梯度下降法
for i in range(nb_epochs):np.random.shuffle(data)for batch in get_batches(data, batch_size=50):params_grad = evaluate_gradient(loss_function, batch, params)params = params - learning_rate * params_grad

随机梯度下降法的主要困难在于第二个问题：学习率的选择。

局部梯度的反方向不一定是函数整体下降的方向。
- 对图像崎岖的函数，尤其是隧道型曲面，梯度下降表现不佳
预定学习率衰减的问题
- 学习率衰减法很难根据当前数据进行自适应。
对于不同的参数采取不同学习率的问题
- 在数据具有一定稀疏性的情况下，希望对不同的特征采取不同的学习率
神经网络训练中，梯度下降法容易被困在鞍点附近的问题
- 比起局部最小值，鞍点最可怕

2.3 随机梯度下降法的优化算法

Q：为什么不适用牛顿法？

1.牛顿法要求计算目标函数的二阶导数(Hessian Matrix)，在高维特征情形下这个矩阵非常巨大，计算和存储都成问题。

2.在使用小批量情形下，牛顿法对于二阶导数的估计噪声太大。

3.在目标函数非凸时，牛顿法更容易收敛到鞍点甚至最大值。

2.3.1 动量法

梯度下降法在狭长的隧道型函数上表现不佳，如下图所示：

函数主体缓缓向右下方下降
在主体方向两侧各有一面高墙，导致垂直于主体方向有更大的梯度
梯度下降法会在隧道两侧频繁振荡

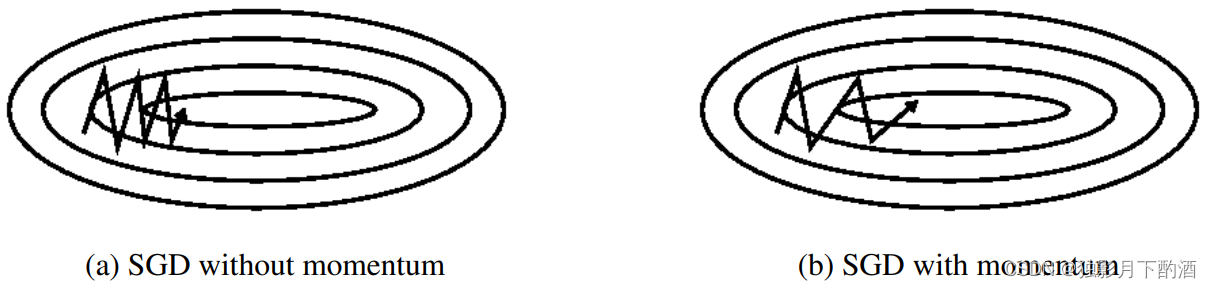
微分学与梯度下降法

动量法每次更新都吸收一部分上次更新的余势：
$vt=γvt−1+η∇θJ(θ)θt=θt−1−vt\\begin{align} &v_t=\\gamma v_{t-1}+\\eta\\nabla_\\theta J(\\theta) \\\\[2ex] &\\theta_t=\\theta_{t-1}-v_t \\end{align}$
这样主体方向的更新就得了更大的保留，从而效果被不断放大。

物理上就像是推一个很重的铁球下山，因为铁球保持了下降主体方向的动量，所以在隧道上沿两侧震荡次数会越来越少。

2.3.2 Nesterov加速梯度下降法

动量法的问题：

从山顶推下的铁球会越滚越快，以至于到了山底停不下来。

我们希望算法聪明一点，可以在达到底部之前就自己刹车了。利用主体下降方向提供的先见之明，预判自己下一步的位置，并到预判位置计算梯度。
$vt=γvt−1+η∇θJ(θ−γvt−1)θ=θ−vt\\begin{align} &v_t=\\gamma v_{t-1}+\\eta\\nabla_\\theta J(\\theta-\\gamma v_{t-1}) \\\\[2ex] &\\theta=\\theta-v_t \\end{align}$
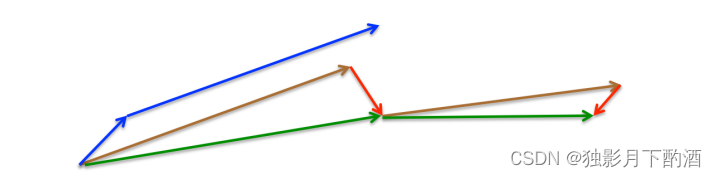
微分学与梯度下降法

动量法首先计算当前的梯度值（图3中的小的蓝色向量），然后在更新的累积梯度（大的蓝色向量）方向上前进一大步，Nesterov加速梯度下降法NAG首先在先前累积梯度（棕色的向量）方向上前进一大步，计算梯度值，然后做一个修正（绿色的向量）。这个具有预见性的更新防止我们前进得太快，同时增强了算法的响应能力，这一点在很多的任务中对于RNN的性能提升有着重要的意义。

2.3.3 Adagrad

梯度下降法在每一步对每一个参数使用相同的学习率，这种一刀切的做法不能有效利用每一个数据集自身的特点。

Adagrad是一种基自动调整学习率的方法：

随着模型的训练，学习率自动衰减
对于更新频繁的参数，采取较小的学习率
对于更新不频繁的参数，采取较大的学习率

为了实现对于更新频繁的参数使用较小的学习率， Adagrad对每个参数历史上的每次更新进行叠加，并以此来做下一次更新的惩罚。

梯度：
$gt,i=∇θJ(θi)g_{t,i}=\\nabla_\\theta J(\\theta_i)$
梯度历史矩阵： $G_t$ 为对角矩阵，其中 $Gt,ii=∑kgk,i2G_{t,ii}=\\sum_k g^2_{k,i}$

参数更新：
$θt+1,i=θt,i−ηGt,ii+ϵ⋅gt,i\\theta_{t+1,i}=\\theta_{t,i}-\\frac{\\eta}{\\sqrt{G_{t,ii}+\\epsilon}}·g_{t,i}$
Adagrad的一个主要缺点是它在分母中累加梯度的平方：由于没增加一个正项，在整个训练过程中，累加的和会持续增长。这会导致学习率变小以至于最终变得无限小，在学习率无限小时，Adagrad算法将无法取得额外的信息。

2.3.4 Adadelta

Adagrad的问题：随着训练的进行，学习速率快速单调递减

在Adadelta中，无需存储先前的 $w$ 个平方梯度，而是将梯度的平方递归地表示成所有历史梯度平方的均值。

定义平均：
$E[g2]t=γE[g2]t−1+(1−γ)gt2E[g^2]_t=\\gamma E[g^2]_{t-1}+(1-\\gamma)g^2_t$
参数更新方式：
$θt+1,i=θt,i−ηE[g2]t,ii+ϵ⋅gt,i\\theta_{t+1,i}=\\theta_{t,i}-\\frac{\\eta}{\\sqrt{E[g^2]_{t,ii}+\\epsilon}}·g_{t,i}$
Adadelta以及一般梯度下降法的另一个问题在于：梯度与参数的单位不匹配

Adadelta使用参数更新的移动平均来取代学习率 $η\\eta$ ，于是参数更新法则为：
$θt+1,i=θt,i−E[Δθ]t−1E[g2]t,ii+ϵ⋅gt,i\\theta_{t+1,i}=\\theta_{t,i}-\\frac{\\sqrt{E[\\Delta_\\theta]_{t-1}}}{\\sqrt{E[g^2]_{t,ii}+\\epsilon}}·g_{t,i}$

2.3.5 Adam

如果把Adadelta里面梯度的平方和看成梯度的二阶矩，那么梯度自身的求和就是一阶矩。

Adam算法在Adadelta的二阶矩基础上又引入了一阶矩，而一阶矩，其实就类似于动量法里的动量
$mt=β1mt−1+(1−β1)gtvt=β2mt−1+(1−β2)gt2\\begin{align} m_t=\\beta_1m_{t-1}+(1-\\beta_1)g_t \\\\[2ex] v_t=\\beta_2m_{t-1}+(1-\\beta_2)g^2_t \\end{align}$
参数更新法则：
$θt+1=θt−ηv^t+ϵm^t\\theta_{t+1}=\\theta_{t}-\\frac{\\eta}{\\sqrt{\\hat v_t}+\\epsilon}\\hat m_t$
注：实际操作中 $v_t$ 和 $m_t$ 采取更好的无偏估计，来避免前几次更新时数据不足的问题。

3.总结

微分学的核心思想：用熟悉且简单的函数对复杂函数进行局部逼近。
梯度方向是函数增长最快的方向
二阶泰勒展开： $f(x0+Δx)=f(x0)+f(1)(x0)⋅Δx+12f(2)(x)⋅Δx2+o(Δx2)f(x_0+\\Delta x)=f(x_0)+f^{(1)}(x_0)·\\Delta x+\\frac{1}{2}f^{(2)}(x)·\\Delta x^2+o(\\Delta x^2)$
梯度下降法：对函数进行一阶逼近寻找函数下降最快的方向。
解决梯度计算问题:批量梯度下降法、随机梯度下降法、小批量随机梯度下降法
批量梯度下降—最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小，但是对于大规模样本问题效率低下。
随机梯度下降—最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向，但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近，适用于大规模训练样本情况。
随机梯度下降算法的优化算法
1. 动量法：适用于隧道型曲面
2. Nesterov加速梯度下降法：动量法的改进，知道什么时候该刹车
3. Adagrad：自动调整学习率，适用于稀疏型数据
4. Adadelta：梯度平方的移动平均来取代全部的历史平方和
5. Adam：在Adadelta的二阶矩的基础上引入一阶矩

本文仅作为个人学习记录使用, 不用于商业用途, 谢谢您的理解合作。

网站制作教程网

微分学与梯度下降法

1.微分学的基本思想和方法

1.1 微分学的核心思想：函数逼近

1.2 微积分的基础语言：极限论

1.3 微分学的基本手法：求导数

1.4 从线性逼近到多项式逼近：泰勒级数

1.5 从低维到高维：多元函数的梯度

2.梯度下降法和牛顿法

2.1 梯度下降法

难点

2.2 随机梯度下降法

2.3 随机梯度下降法的优化算法

2.3.1 动量法

2.3.2 Nesterov加速梯度下降法

2.3.3 Adagrad

2.3.4 Adadelta

2.3.5 Adam

3.总结

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签

微分学与梯度下降法

1.微分学的基本思想和方法

1.1 微分学的核心思想：函数逼近

1.2 微积分的基础语言：极限论

1.3 微分学的基本手法：求导数

1.4 从线性逼近到多项式逼近：泰勒级数

1.5 从低维到高维：多元函数的梯度

2.梯度下降法和牛顿法

2.1 梯度下降法

难点

2.2 随机梯度下降法

2.3 随机梯度下降法的优化算法

2.3.1 动量法

2.3.2 Nesterov加速梯度下降法

2.3.3 Adagrad

2.3.4 Adadelta

2.3.5 Adam

3.总结

相关问题

公告

DeepSeek全套部署资料免费下载

免费可商用字体批量下载

标签