学习目标：

学习龙格-库塔法的具体明确的学习目标可以有以下几点：

1. 理解龙格-库塔法的基本思想和原理：我们应该了解龙格-库塔法的数值求解思想和数值误差的概念，包括截断误差和稳定性等基本概念，并且要熟悉龙格-库塔法的计算公式和计算过程。

2. 能够熟练地应用龙格-库塔法：我们应该能够熟练地应用龙格-库塔法来求解常微分方程组，并且要掌握如何选择合适的步长和算法参数等，以获得更加准确的数值解。

3. 熟悉龙格-库塔法的各种变种和改进方法：我们应该了解龙格-库塔法的各种变种和改进方法，例如四阶龙格-库塔法、自适应步长控制方法等，并且要掌握如何选择适当的方法来应对不同的问题和需求。

4. 能够进行数值实验和分析：我们应该能够设计和实现一些简单的数值实验，以验证龙格-库塔法的性能和精度，并且要能够进行数值误差分析和比较，以评估龙格-库塔法的优缺点。

综上所述，学习龙格-库塔法的具体明确的学习目标包括理解基本原理和思想、熟练应用算法、熟悉改进方法和自适应步长控制等、能够进行数值实验和误差分析等方面。

 6.2.1 龙格-库塔法

龙格-库塔法是一种经典的常微分方程数值解法，其构造基于求解常微分方程的初值问题。其基本思想是在每个步长内用一定次数的导数信息来近似表示方程的解，从而得到一组离散的数值解。

具体来说，龙格-库塔法的构造原理如下：

1. 将时间区间 $[t_0, T]$ 分为 $n$ 个小区间，其中 $t_0$ 表示初始时间点，$T$ 表示终止时间点，$n$ 表示步数。

2. 在每个小区间内，采用一定的方式来逼近微分方程的解。龙格-库塔法采用了一组系数来逼近解函数和导数函数的值，从而得到一个数值解。

3. 对于每个小区间，龙格-库塔法首先根据当前时刻 $t_n$ 和当前解值 $y_n$，计算出导数信息 $f(t_n, y_n)$。然后通过多次计算，逐步近似出 $y_{n+1}$ 的值。

4. 龙格-库塔法的计算过程中，通过不断迭代来提高数值解的精度。具体来说，每次迭代都会计算出一个局部截断误差，然后根据这个误差和一定的策略，来调整步长和迭代次数，从而达到更高的精度。

总的来说，龙格-库塔法的构造原理就是通过逼近微分方程的解和导数信息，不断迭代求解方程的数值解，同时通过自适应调整步长和迭代次数，来提高数值解的精度和稳定性。

6.2.2 经典龙格-库塔法

经典的龙格-库塔法通常是指四阶龙格-库塔法，也称作RK4方法。这是一种经典的常微分方程数值解法，被广泛应用于各种领域，比如天文学、物理学、工程学等。

RK4方法的计算过程如下：

1. 将时间区间 $[t_0, T]$ 分为 $n$ 个小区间，其中 $t_0$ 表示初始时间点，$T$ 表示终止时间点，$n$ 表示步数。设 $h=(T-t_0)/n$ 表示步长。

2. 对于第 $i$ 个小区间，计算出 $t_i=t_0+ih$，$y_i$ 是解函数在 $t_i$ 处的近似值。初始值 $y_0$ 已知。

3. 对于每个小区间，RK4方法需要计算出 $y_{i+1}$ 的近似值。具体来说，可以分为以下四个步骤：

   (1) 计算斜率 $k_1=f(t_i, y_i)$

   (2) 计算斜率 $k_2=f(t_i+\\frac{h}{2}, y_i+\\frac{h}{2}k_1)$

   (3) 计算斜率 $k_3=f(t_i+\\frac{h}{2}, y_i+\\frac{h}{2}k_2)$

   (4) 计算斜率 $k_4=f(t_i+h, y_i+hk_3)$

   其中，$f(t, y)$ 表示微分方程的右侧，$k_1$，$k_2$，$k_3$ 和 $k_4$ 分别是四个不同时间点的导数值。

4. 根据四个斜率的加权平均值，计算出 $y_{i+1}$ 的近似值：

   

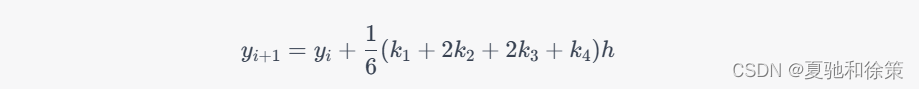
5. 重复以上步骤，计算出整个时间区间上的数值解。

需要注意的是，虽然RK4方法是一种高阶方法，但其计算量也比较大，特别是在需要高精度的情况下。此外，RK4方法也存在一些限制条件，比如微分方程的解函数必须具有一定的光滑性质，步长也需要根据微分方程的性质来选择。

 6.2.3 步长的自动选择

步长的自动选择是为了解决数值解精度和计算效率之间的矛盾而提出的一种方法。其基本思想是根据当前的解函数和近似解函数之间的差异来自适应地选择步长，从而在保证精度的前提下尽可能地减小计算量。

步长自适应选择的基本流程如下：

1. 根据当前的解函数和近似解函数之间的差异，估计出当前的截断误差。

2. 根据截断误差和预先给定的精度要求，计算出理论上的最大步长。

3. 计算出当前的局部误差，比较局部误差和截断误差的大小，以此为依据来确定下一步的步长。

具体的步长自适应选择算法有很多，比如Dormand-Prince方法、Adams-Bashforth-Moulton方法等。其中，Dormand-Prince方法是一种常用的步长自适应选择算法，其基本思路是利用四阶和五阶两种不同精度的龙格-库塔法来计算数值解，并根据两个结果的差异来选择下一步的步长。

 我的理解：

步长的自动选择是一种数值方法中的策略，它的目的是在保证数值解的精度的前提下，尽可能地减小计算量。在实际应用中，我们往往需要计算大量的数值解，而这些数值解的精度要求可能不同，因此需要根据实际情况来选择步长。步长的自动选择算法通常基于当前的解函数和近似解函数之间的差异来适应地调整步长，从而在保证数值解精度的前提下尽可能地减小计算量。步长自适应选择算法是数值计算中的一种重要技术，它可以提高计算效率和数值解的精度，广泛应用于科学计算、工程设计等地方。

 总结：

龙格-库塔法是一种数值解微分方程的常用方法，其主要优点是精度高、适用范围广、易于实现等。以下是龙格-库塔法的重点、难点和易错点：

重点：

1. 龙格-库塔法是一种数值解微分方程的迭代方法，其基本思路是利用一系列的中间量来逐步逼近真实解。

2. 龙格-库塔法通常需要通过一定的数学推导和计算来确定中间量和逼近公式，因此需要一定的数学功底和计算能力。

3. 龙格-库塔法的精度可以通过调整步长来控制，步长的自动选择是龙格-库塔法中的一个重要技术。

难点：

1. 龙格-库塔法需要在每个时间步长上进行大量的计算，因此计算效率较低，尤其是在高阶方法中。

2. 龙格-库塔法的实现过程中，需要注意数值误差的积累问题，以避免数值解的不稳定和发散。

3. 在实际应用中，龙格-库塔法的适用范围需要根据问题的具体情况来选择，否则可能会导致数值解的不准确。

易错点：

1. 龙格-库塔法中的迭代公式较为复杂，容易出错，需要仔细检查每个中间量的计算过程。

2. 步长的自动选择需要根据实际问题来选择，如果选择不当可能会导致数值解的不准确或计算量过大。

3. 龙格-库塔法在高维问题中的应用较为困难，因为其计算量和计算复杂度都会随着维度的增加而增加。