2023第十四届蓝桥杯 C/C++大学生A组省赛 满分题解

写在前面
以下代码,目前均可通过民间OJ数据(dotcpp & New Online Judge),
两个OJ题目互补,能构成全集,可以到对应链接下搜题提交(感谢OJ对题目的支持)
如果发现任何问题,包含但不限于算法思路出错、OJ数据弱算法实际超时、存在没考虑到的边界情况等,请及时联系作者

题解
A.幸运数(模拟)
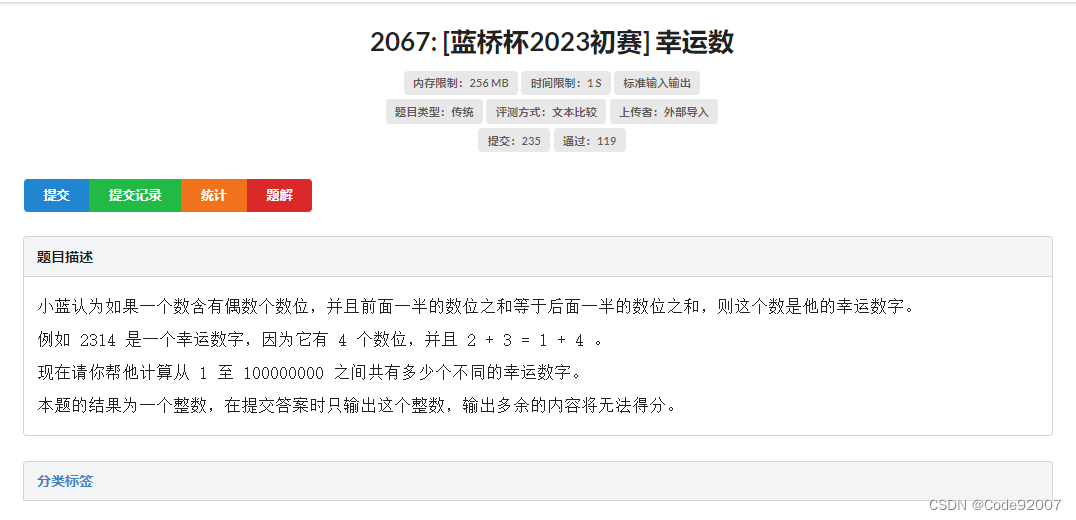
题面
题解
由于是填空题,按题意本地暴力,几秒就跑出来结果了,直接交结果
代码
#include<bits/stdc++.h>
using namespace std;
int ans;
int main(){/*for(int i=1;i<=100000000;++i){int cnt=0;for(int j=i;j;j/=10)cnt++;if(cnt&1)continue;int sum=0,now=0;for(int j=i;j;j/=10){now++;if(now<=cnt/2)sum+=j%10;else sum-=j%10;}if(!sum)ans++;}printf("%d\\n",ans);*/puts("4430091");return 0;
}B.有奖问答(搜索/dp)
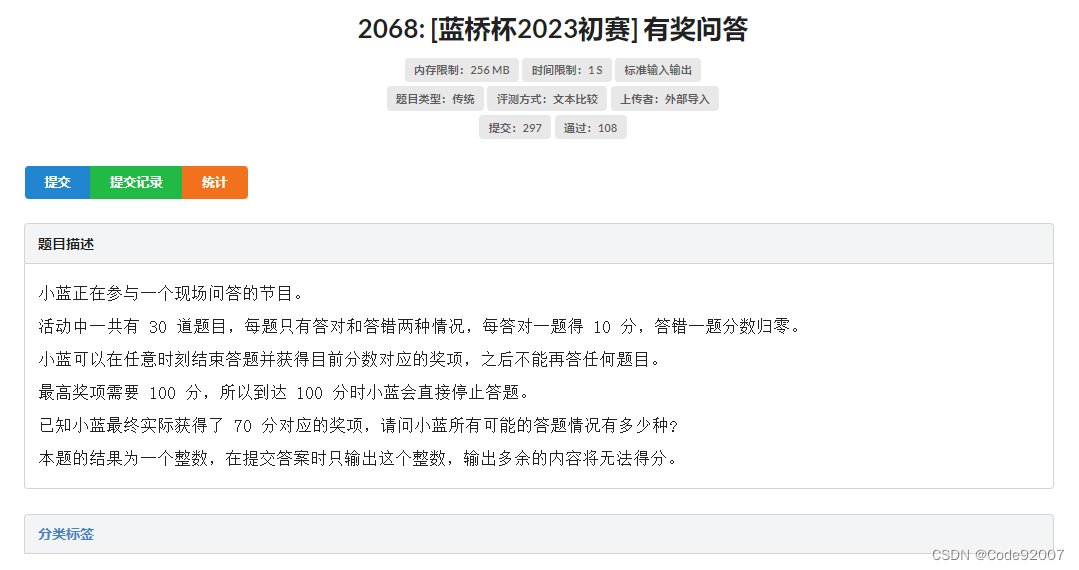
题面
题解
1. 搜索:2的30次方种可能,每次要么+10要么清零,遇到100分时,直接return,几秒跑出来结果后,直接交结果
2. dp:dp[i][j]表示前i轮过后分数为j的方案数,注意中间可以随时停止
代码(dp)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[31][101],ans;
int main(){dp[0][0]=1;for(int i=0;i<30;++i){for(int j=0;j<100;j+=10){if(!dp[i][j])continue;if(j<90)dp[i+1][j+10]+=dp[i][j];dp[i+1][0]+=dp[i][j];}ans+=dp[i+1][70];}printf("%lld\\n",ans);//puts("4165637");return 0;
}C.平方差(构造/规律)
题面

题解
打表或构造发现,形如4k+2的数无法被表示,
统计[l,r]的答案,前缀和作差,转化为[1,r]的答案减去[1,l-1]的答案
而[1,x]中,形如4k+2的数的个数为(x+2)/4
证明的话,x=(y+z)(y-z),注意到y+z和y-z同奇偶,
1. y+z为奇数时,x为奇数;y+z为偶数时,x为4的倍数,这表明4k+2无法被取到
2. ,
,这表明奇数和4的倍数均能被取到
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=500;
bool vis[N];
int l,r;
int cal(int x){return x-(x+2)/4;
}
int main(){/*for(int i=0;i<=50;++i){for(int j=0;j<=i;++j){int v=i*i-j*j;if(v>=0 && v<N)vis[v]=1;}}for(int i=0;i<=100;++i){if(!vis[i])printf("i:%d\\n",i);}*/scanf("%d%d",&l,&r);printf("%d\\n",cal(r)-cal(l-1));return 0;
}
//x=(y+z)(y-z)
//2k+1=(k+1)^2-k^2
//4k=(k+1)^2-(k-1)^2D.更小的数(区间dp)
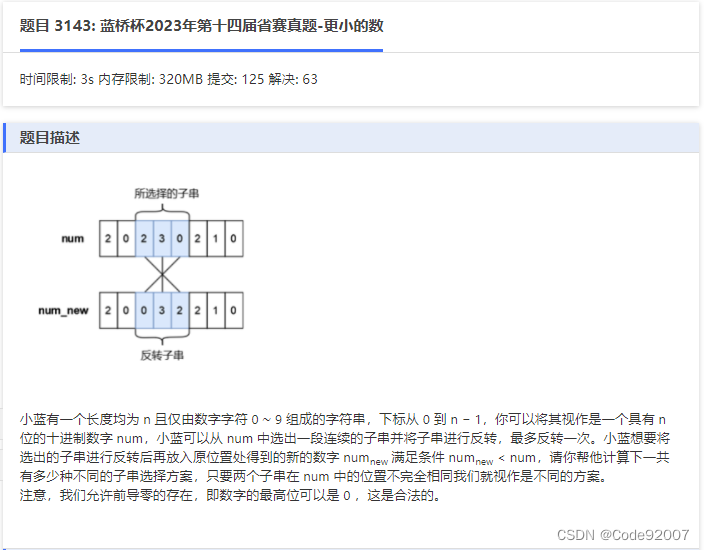
题面
题解
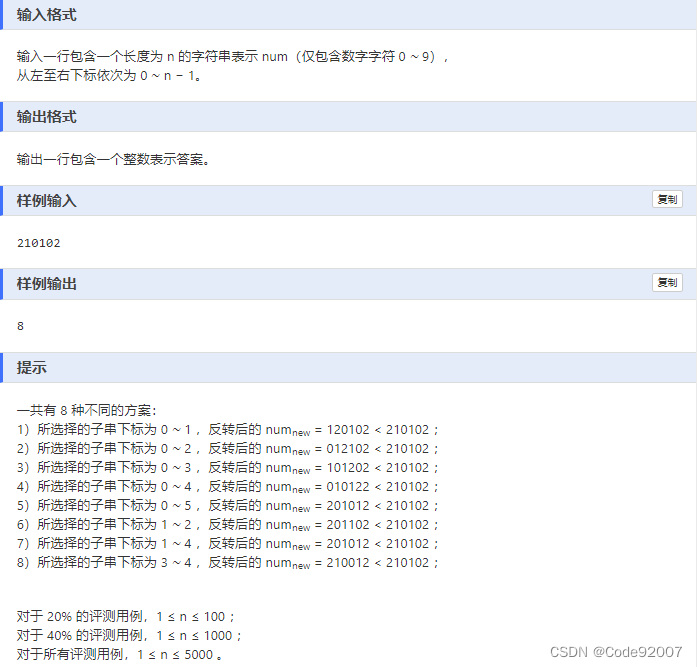
未反转的段仍相同不用关注,只需关注反转的段,
记反转前的串为old(即num串),之后的串为new
运用递归/记忆化搜索的思想,有以下几种情况
1. 当i=j时,new[i,j]不小于old[i,j]
2. 当i+1=j时,new[i,j]小于old[i,j],当且仅当new[i]<old[i],即num[j]<num[i]
3. 否则,
①若num[j]<num[i],new[i,j]一定小于old[i,j]
②若num[j]=num[i],则可以去掉这两个字母,只需比较new[i+1,j-1]和old[i+1,j-1]
③若num[j]>num[i],new[i,j]一定大于old[i,j]
从短串递推到长串,就是区间dp了,当然直接写记忆化搜索也行
代码中,dp[i][j]=1表示反转后更小,=0表示反转后大于等于原来
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e3+10;
int n,dp[N][N],ans;
char s[N];
int main(){scanf("%s",s);n=strlen(s);for(int len=2;len<=n;++len){for(int l=0;l+len-1<n;++l){int r=l+len-1;if(s[l]>s[r])dp[l][r]=1;else if(s[l]==s[r])dp[l][r]=dp[l+1][r-1];ans+=(dp[l][r]==1);}}printf("%d\\n",ans);return 0;
}
//4321
//1234E.更小的数(树上莫队/启发式合并)
题面
题解
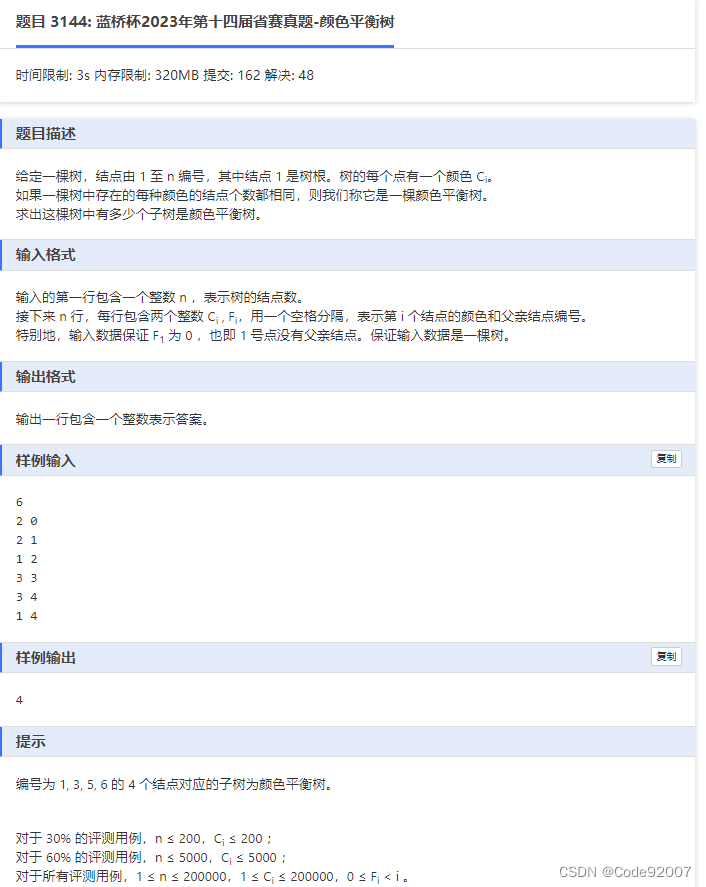
1. 树上莫队:树上莫队=莫队+dfs序。建树后求dfs序,每个子树对应的dfs区间就是一个询问区间,将询问区间排序后套用莫队,维护当前颜色i出现的次数now[i]、出现次数为i的颜色种类数freq[i]。任取区间内出现的一种颜色x,若now[x]*freq[now[x]]=区间长度则合法,否则不合法。复杂度O(nsqrt(n))。
2. 启发式合并:可以维护相同的东西,只是套了个启发式合并的壳。重儿子直接继承当前维护的信息,把轻儿子维护的信息往重儿子上合并,由于每个点至多出现在log个轻儿子所在的子树里,复杂度O(nlogn)。
代码(树上莫队)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+10;
int n,m,c[N],f,in[N],out[N],tot,id[N],pos[N],sz;
int now[N],freq[N],ans;
map<int,int>vis;
vector<int>e[N];
struct node{int l,r;
}q[N];
void add(int col,int v){freq[now[col]]--;now[col]+=v;freq[now[col]]++;
}
bool operator<(node a,node b){if(pos[a.l]==pos[b.l]){if(pos[a.l]&1)return a.r>b.r;else return a.r<b.r;}return a.l<b.l;
}
void dfs(int u){in[u]=++tot;id[tot]=u;for(auto &v:e[u]){dfs(v);}out[u]=tot;q[++m]={in[u],out[u]};
}
int main(){scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d%d",&c[i],&f);if(!vis.count(c[i])){vis[c[i]]=1;freq[0]++;}if(i>1)e[f].push_back(i);}dfs(1);sz=(int)sqrt(n);for(int i=1;i<=n;++i){pos[i]=1+(i-1)/sz;}sort(q+1,q+n+1);int l=1,r=1;add(c[1],1);for(int i=1;i<=n;++i){for(;r<q[i].r;r++)add(c[id[r+1]],1);for(;r>q[i].r;r--)add(c[id[r]],-1);for(;l<q[i].l;l++)add(c[id[l]],-1);for(;l>q[i].l;l--)add(c[id[l-1]],1);int col=c[id[l]],cnt=now[col],f=freq[cnt];if(f*cnt==r-l+1)ans++;}printf("%d\\n",ans);return 0;
}
/*
6
2 0
2 1
1 2
3 3
3 4
1 4
*/F.买瓜(折半枚举+三进制枚举/枚举子集的子集)
题面
题解
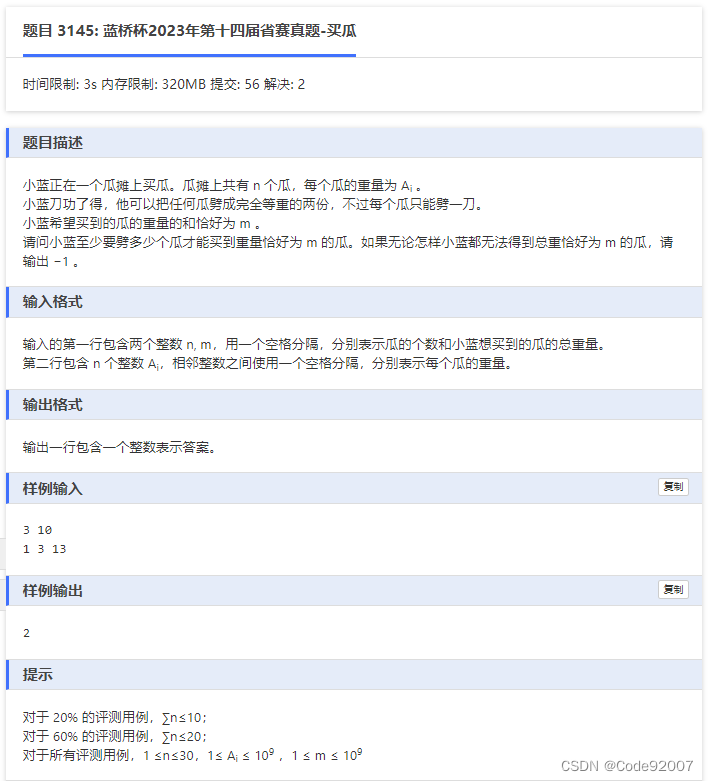
每个西瓜三种选择:不选,选但不劈,选且劈两半。
直接三进制枚举的话,3的30次方,复杂度爆炸,
考虑拆成两半枚举(折半枚举,也叫meet-in-middle)
分别维护3的15次方大小的集合a、b,
答案只可能完全来自a、或者完全来自b、或者ab各一部分
ab各一部分的话,在枚举b集合的元素x时,到a集合内查对应元素m-x是否存在
复杂度,2s时间比较极限,难以通过,而瓶颈主要在集合查的这个log,
所以手写哈希(开散列),将15这个常数再压一压,就可以通过了
256M空间其实也比较极限,哈希模数那个数组不要开太大(调小了TLE调大了MLE)
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
#define fi first
#define se second
const int N=32,M=1<<15,mod=19260817,S=14348907;
int n,bit[M];
int head[mod],nex[S],cnt;
P b[S];
ll m,a[N],f[M],g[M],sum;
inline void upd(int x,int v){int u=x%mod;for(int i=head[u];i;i=nex[i]){if(b[i].fi==x){b[i].se=min(b[i].se,v);return;}}b[++cnt]=P(x,v);nex[cnt]=head[u];head[u]=cnt;
}
inline int cal(int x){int u=x%mod;for(int i=head[u];i;i=nex[i]){if(b[i].fi==x)return b[i].se;}return N;
}
int sol(){if(sum==m)return 0;if(n==1){if(a[0]/2==m)return 1;return -1;}int ans=N;for(int i=1;i<M;++i){bit[i]=bit[i>>1]+(i&1);}int l=n/2,lb=1<<l,r=n-n/2,rb=1<<r;for(int i=0;i<l;++i){f[1<<i]=a[i];}for(int i=1;i<lb;++i){int x=i&-i;f[i]=f[x]+f[i^x];if((f[i]>>1)>m)continue;for(int j=i;;j=(j-1)&i){ll v=(f[j]>>1)+f[j^i];if(v<=m){if(v==m)ans=min(ans,bit[j]);else upd((int)v,bit[j]);}if(!j)break;}}for(int i=0;i<r;++i){g[1<<i]=a[l+i];}for(int i=1;i<rb;++i){int x=i&-i;g[i]=g[x]+g[i^x];if((g[i]>>1)>m)continue;for(int j=i;;j=(j-1)&i){ll v=(g[j]>>1)+g[j^i];if(v<=m){if(v==m)ans=min(ans,bit[j]);else ans=min(ans,cal((int)(m-v))+bit[j]);}if(!j)break;}}if(ans>n)ans=-1;return ans;
}
int main(){scanf("%d%lld",&n,&m);m*=2;for(int i=0;i<n;++i){scanf("%lld",&a[i]);a[i]*=2;sum+=a[i];}printf("%d\\n",sol());return 0;
}G.网络稳定性(kruskal重构树)
题目

题解
kruskal重构树裸题,
重构树听上去高端,实则就是在kruskal建最大生成树的过程中额外建点、赋权
比如,u和v当前不在一个集合里,通过w这条边合并时,
新开一个点x,令x是u和v的父亲,而x的权值为w,
查询时,查u和v的lca的权值即可,即为最大连通路径上的最小连通权值
因为按权值从大到小遍历,已经通过权值大的边,使得点之间尽可能能连通了
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4e5+10,M=3e5+10,K=20;
int n,m,q,u,v,par[N],a[N],f[N][K],dep[N];
bool vis[N];
vector<int>E[N];
struct edge{int u,v,w;
}e[M];
int find(int x){return par[x]==x?x:par[x]=find(par[x]);
}
bool cmp(edge a,edge b){return a.w>b.w;
}
void dfs(int u,int fa){vis[u]=1;f[u][0]=fa;dep[u]=dep[fa]+1;for(auto &v:E[u]){if(v==fa)continue;dfs(v,u);}
}
int lca(int u,int v){if(dep[u]<dep[v])swap(u,v);int d=dep[u]-dep[v];for(int i=K-1;i>=0;--i){if(d>>i&1)u=f[u][i];}if(u==v)return u;for(int i=K-1;i>=0;--i){if(f[u][i]!=f[v][i])u=f[u][i],v=f[v][i];}return f[u][0];
}
int main(){scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n+m;++i){par[i]=i;}for(int i=1;i<=m;++i){scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);}sort(e+1,e+m+1,cmp);int cur=n;for(int i=1;i<=m;++i){int u=e[i].u,v=e[i].v,w=e[i].w;u=find(u),v=find(v);if(u==v)continue;++cur;par[u]=par[v]=cur;E[cur].push_back(u);E[cur].push_back(v);a[cur]=w;}for(int i=cur;i>=1;--i){if(!vis[i])dfs(i,0);}for(int j=1;j<K;++j){for(int i=1;i<=cur;++i){f[i][j]=f[f[i][j-1]][j-1];}}while(q--){scanf("%d%d",&u,&v);if(find(u)!=find(v)){puts("-1");continue;}printf("%d\\n",a[lca(u,v)]);}return 0;
}
/*
5 4 3
1 2 5
2 3 6
3 4 1
1 4 3
1 5
2 4
1 3
*/H. 异或和之和(按位计算贡献)
题目
题解
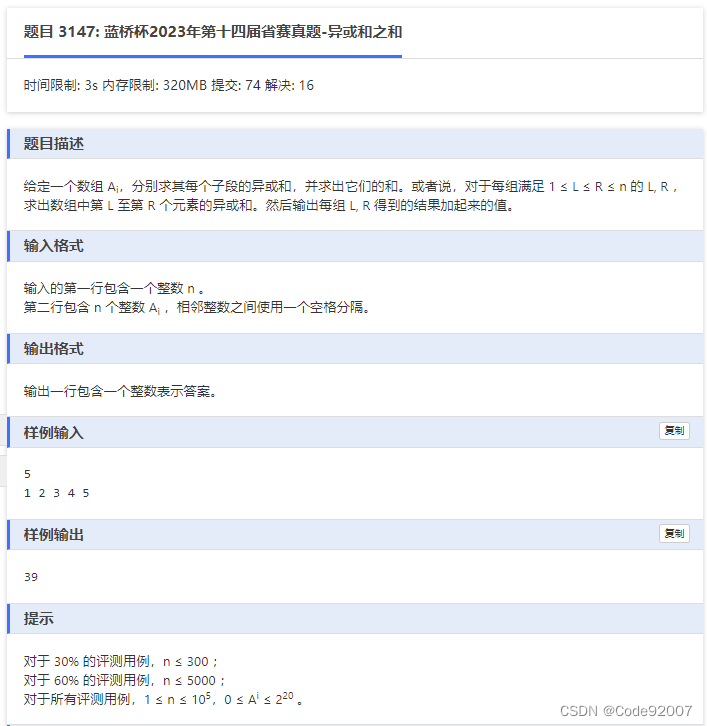
按每个二进制位i考虑,从而转化为0、1序列的问题
一个子段[l,r]在第i位有贡献,当且仅当[l,r]内第i位出现的次数为奇数次,
前缀和做差[l,r]=[1,r]减[1,l-1],所以维护当前有多少个前缀是奇数,有多少个前缀是偶数
[l,r]为奇数,若[1,r]为偶数则要求[1,l-1]为奇数,反之同理,
枚举每个右端点,统计与其对应的有贡献的左端点,计算答案
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,a[N],sum[2];
ll ans;
int main(){scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d",&a[i]);}for(int i=0;i<=20;++i){sum[0]=1,sum[1]=0;int now=0;ll all=0;for(int j=1;j<=n;++j){int v=a[j]>>i&1;now^=v;all+=sum[now^1];sum[now]++;}ans+=all*(1ll<<i);}printf("%lld\\n",ans);return 0;
}
/*
5
1 2 3 4 5
*/I. 异或和之和(搜索)
题面
题解
最担心被卡掉的一个题,由于唯一解的数据似乎不太好造,导致也不太好在本地测时间
写状压的话感觉总难免需要关注三行的有效状态,复杂度好像更没有办法保证,所以写了搜索剪枝
总体思路还是枚举每一位填0还是填1,加入了校验机制,以及搜到解之后直接return
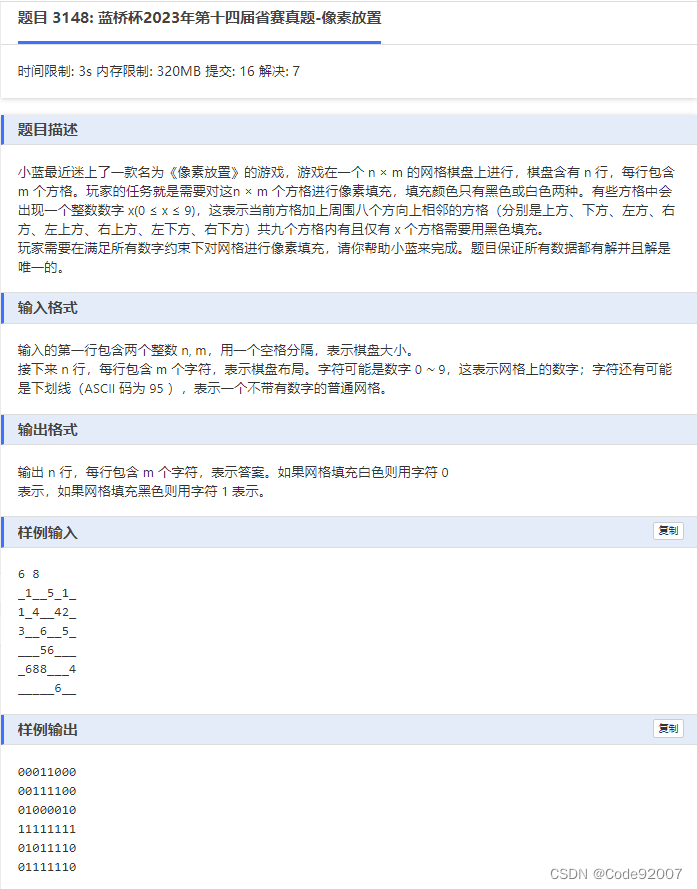
a[i][j]:原图转化过来的数字,下划线转成了INF
b[i][j]:当前填的答案数组
cur[i][j]:(i,j)本身及(i,j)周围一圈合法位置中,当前填了几个1
填一个数时,考虑它本身及周围一圈的合法位置(最多9个)
校验机制是:
1. 如果当前填了这个数,导致超过上限,即cur[i][j]>a[i][j],则不合法
2. 如果当前填的格子,是格子(i,j)管辖的最后一个格子,填完这个数后,a[i][j]和cur[i][j]不等,则也不合法
代码
#include<bits/stdc++.h>
using namespace std;
const int S=15,INF=0x3f3f3f3f;
int n,m,a[S][S],b[S][S],cur[S][S];
char s[S][S];
bool ok;
bool in(int x,int y){return 0<=x && x<n && 0<=y && y<m && a[x][y]!=INF;
}
bool can(int x,int y,int v){for(int i=-1;i<=1;++i){for(int j=-1;j<=1;++j){int nx=x+i,ny=y+j;if(in(nx,ny) && cur[nx][ny]+v>a[nx][ny])return 0;}}if(in(x-1,y-1) && cur[x-1][y-1]+v<a[x-1][y-1])return 0;if(x==n-1 && in(x,y-1) && cur[x][y-1]+v<a[x][y-1])return 0;if(y==m-1 && in(x-1,y) && cur[x-1][y]+v<a[x-1][y])return 0;return 1;
}
void dfs(int x,int y){//cnt++;if(x==n && y==0){ok=1;for(int i=0;i<n;++i){for(int j=0;j<m;++j){printf("%d",b[i][j]);}puts("");}return;}if(ok)return;for(int v=0;v<=1;++v){if(ok)return;if(can(x,y,v)){b[x][y]=v;if(v){for(int i=-1;i<=1;++i){for(int j=-1;j<=1;++j){int nx=x+i,ny=y+j;if(!in(nx,ny))continue;cur[nx][ny]++;}}}if(y==m-1)dfs(x+1,0);else dfs(x,y+1);if(v){for(int i=-1;i<=1;++i){for(int j=-1;j<=1;++j){int nx=x+i,ny=y+j;if(!in(nx,ny))continue;cur[nx][ny]--;}}}}}
}
int main(){scanf("%d%d",&n,&m);for(int i=0;i<n;++i){scanf("%s",s[i]);for(int j=0;j<m;++j){a[i][j]=INF;if(s[i][j]!='_')a[i][j]=s[i][j]-'0';}}dfs(0,0);//printf("cnt:%d\\n",cnt);return 0;
}J.翻转硬币(整除分块+杜教筛)
题面
题解
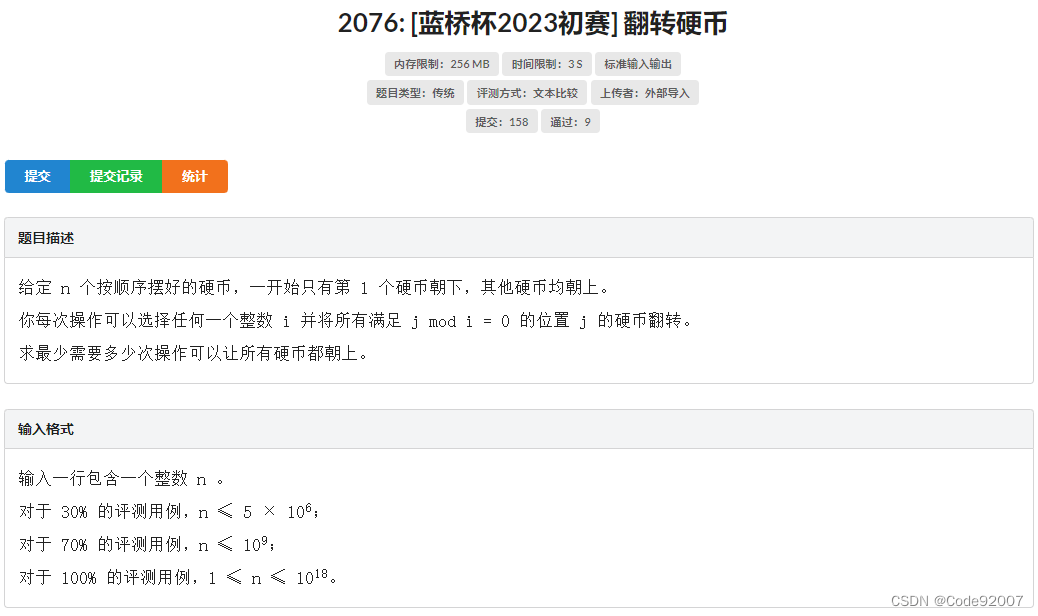
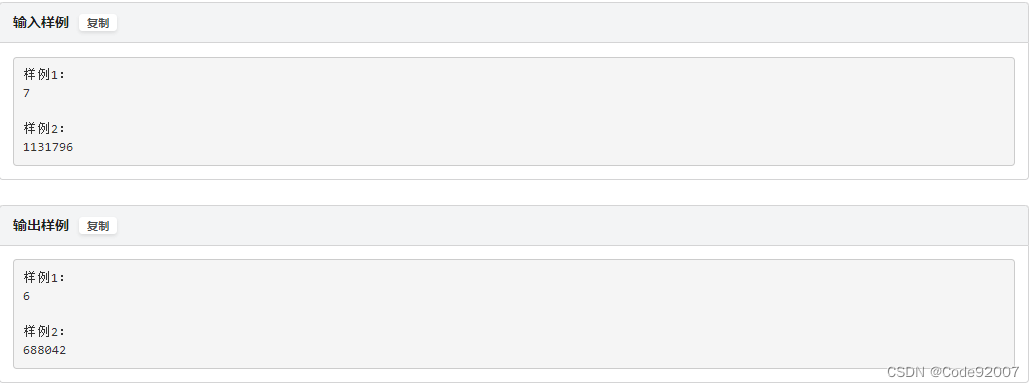
1. 5e6,可以考虑埃筛枚举因数,x需要翻当且仅当x的真因数翻了奇数次
2. 1e9,观察5e6时的式子,其实就是莫比乌斯函数mu[i]%2下的值,即只有0和1两种情况,此时可以认为是mu[i]的绝对值或者mu[i]的平方,然后直接套杜教筛
3. 1e18,观察1e9时的式子或思考莫比乌斯函数的定义,只有包含完全平方因子的数的mu值才为0,所以考虑对平方因子容斥,即为所求,
直接整除分块(数论分块)的话是的,不能接受
于是类似杜教筛预处理前缀和的操作,
这里实际预处理部分的答案(询问是单组的,现算这部分效果是一样的)
用杜教筛预处理mu的前缀和,后面[1e6,1e9]的部分用整除分块配合mu的区间和解决
【SSL 2402】最简根式(杜教筛)(整除分块)_SSL_TJH的博客-CSDN博客,与这个题类似
复杂度感觉是的,但据uoj群友说是
的,就不太懂了…
实际预处理到1e6交new oj也是会t的,改到1e7才过
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e7+10;
bool ok[N];
int pr[N],mu[N],cnt,up;
map<int,int>smu;
ll n,ans[N];
void sieve(ll n){mu[1]=1;for(ll i=2;i<N;++i){if(!ok[i]){pr[cnt++]=i;mu[i]=-1;}for(int j=0;j<cnt;++j){ll k=i*pr[j];if(k>=N)break;ok[k]=1;if(i%pr[j]==0){mu[k]=0;break; }mu[k]=-mu[i];}}for(int i=1;i<N;++i){ans[i]=mu[i]*(n/i/i);}for(int i=2;i<N;++i){mu[i]+=mu[i-1];ans[i]+=ans[i-1];}
}
int djsmu(int n){if(n<N)return mu[n];if(smu.count(n))return smu[n];int ans=1;for(int l=2,r;l<=n;l=r+1){r=n/(n/l);ans=ans-(r-l+1)*djsmu(n/l);if(r==n)break;}return smu[n]=ans;
}
ll cal(ll n){int sq=sqrt(n);if(sq<N)return ans[sq];ll l=2;for(;l*l*l<=n;l++);ll res=ans[l-1];for(ll r;l*l<=n;l=r+1){ll v=n/l/l;r=sqrt(n/v);res+=v*(djsmu(r)-djsmu(l-1));}return res;
}
int main(){scanf("%lld",&n);sieve(n);printf("%lld\\n",cal(n));return 0;
} 

