Point-to Analysis指针分析（1）

大家好呀，今天咱们聊一个听起来有点复杂，但其实很有趣的主题——指针分析！特别是那种“上下文不敏感分析”，听起来像是个侦探，但其实是个编程概念，别紧张，我来带大家简单了解一下。

看起来复杂，但其实很简单
指针分析嘛，就是研究变量指向哪里的学问。上下文不敏感分析呢，就像个大大咧咧的警察，不计较细节，只抓住“大概率正确”的情况。比如说，a指向了b，c也指向了b，那警察说：“管他呢，反正a和c都指向了b附近！”这种分析方式虽然可能不够精确，但是超级快，特别适合“速战速决”的场景。

你可能会问：这有啥用？
其实，这种分析方法在编译器优化、代码分析工具里特别有用。比如，想优化内存访问，或者检测内存泄漏，这时候不需要知道每个变量绝对指向哪里，只需要大概的范围就行。就像开车导航，你可能不在意具体哪条小路，只要知道大概方向不跑偏就行。

安德森的算法是咋回事？
安德森的算法是分析C语言指针的经典方法，它通过构建约束图来解决指针指向问题。比如，代码中有a = &b，b = &c，a = b，那么Pts(a)就包含了b和c的地址。听起来有点抽象，但其实就是用数学里的集合来表示可能性，就像在玩“可能指向”的游戏一样。

你可能会疑惑：为什么不精确？
因为不敏感分析“不太较真”嘛，它只关心“肯定正确”的结果，不管有多“宽泛”。比如，假设a可能指向b或者c，那它就直接认为a指向了b和c。这种做法虽然“偷懒”了点，但效率高，还能避免复杂的上下文判断。

举个栗子更清晰
比如代码：
`c
p = &a;
q = &b;
*p = q;
r = &c;
s = p;
t = *p;
*s = r;
`
按照安德森的算法，我们会翻译成约束关系：
`
p ⊇ {a}, q ⊇ {b}, *p ⊇ q, r ⊇ {c}, s ⊇ p, t ⊇ *p, *s ⊇ r
`
这样，通过约束图，我们就能一步步推导出每个变量的指向，就像在玩一个逻辑推理游戏一样。

整体而言：简单高效，但不完美
上下文不敏感分析就像个大大咧咧的“差不多先生”，它不追求完美，但效率奇高，适合快速分析。当然，它也有缺点，比如不够精确，可能会漏掉一些具体情况。但如果你只需要一个大致的方向，它绝对是个好帮手。

你可能会想：如何提升精确度？
如果你想更精确，就得用上下文敏感分析，比如使用“基于流的分析”或者“路径敏感分析”，但这些方法复杂度会大大提高，就像从开普车换成了F1赛车，速度快了，但维护起来也麻烦了。

整体而言，指针分析是个挺有意思的主题，特别是像安德森的算法这种经典方法，既简单又高效，下次遇到类似问题，不妨试试看哦！

Point-to Analysis指针分析（1）_音程的博客-CSDN博客

前言

指针分析是一个非常复杂的工作，这些工作很多方向，比如是否是上下文敏感分析或上下文不敏感分析，显然，这难易度是不一样地。比如下图。对于同一段代码，敏感性分析如蓝色，不敏感分析如红色。

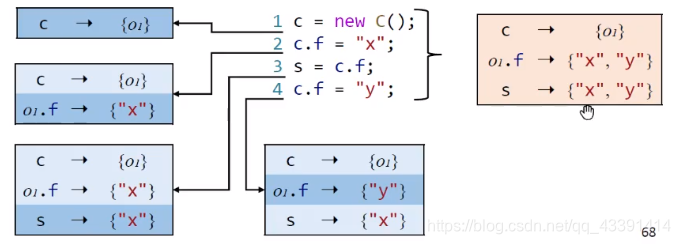
 相比之下，不敏感分析不在乎语句的顺序，比如2，4两个语句换一下位置，得到的结果还是一样的，同时也不要求结果是否精确。

不敏感分析特点：安全。
即确保召回那个唯一正确的值就好，而不管精确不精确，是不是多了。

下面我们要讨论的就是不敏感分析。所以有些语句我们是不会管的，比如：

即，我们只管那些赋值的，和指针相关的语句。从而将此工作得到了大大简化。

 Anderson’s pointer analysis

这个指针分析的算法很有名，是分析C语言的，但是思想都是通用的，下面开始介绍。

基础

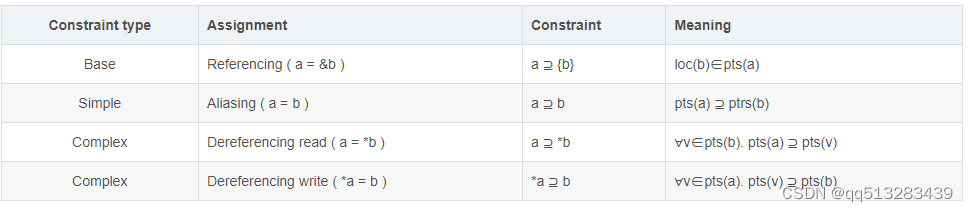
解释：我们暂时先不看第一列和第三列，其他的应该很好理解。 

• loc(b)表示b的地址。
• pts(a)：point-to sets(a)，表示a的可能指向集合，千万注意是可能指向，别忘了我们是做不敏感分析。即如果a=&b,a=&c，那么有pts(a)={loc(b),loc(c)}。
• ∈，⊇，这个和数学中集合的概念一致，就是属于和子集关系的意思。
• 以第2行为例，有pts(a) ⊇ ptrs(b)，为什么？举个例子你就明白了，如果有：a=&d,b=&c,a=b。那么pts(b)={loc(c)},pts(a)={loc(c),loc(d)}。所以明白了为什么pts(a)可能比pts(b)集合更大了吧，因为a=b把b的指向全部给了a，但是a可能还有其他的指向啊！

约束图

现在我们要做一些前期工作，并且要开始看上面那个表的第一列和第三列。举例来说，如果有代码：

p = &a;q = &b;*p = q;r = &c;s = p;t = *p;*s = r;

我们按照上面表的第3列翻译成下面，叫做约束：

p  ⊇ {a}, q  ⊇ {b}, *p ⊇ q, r ⊇ {c}, s ⊇ p, t ⊇ *p, *s ⊇ r

我们可以开始根据上面的表格创建初始约束图，其中基本(base)约束和(simple)约束是创建初始约束图的基础。初始约束图的创建分为如下三步：

• 首先为程序中的每个变量建立一个节点
• 后根据基本(base)约束标注节点的指向集
• 每一个初始的简单约束(simple)建立一条有向边

可以得到如下图：

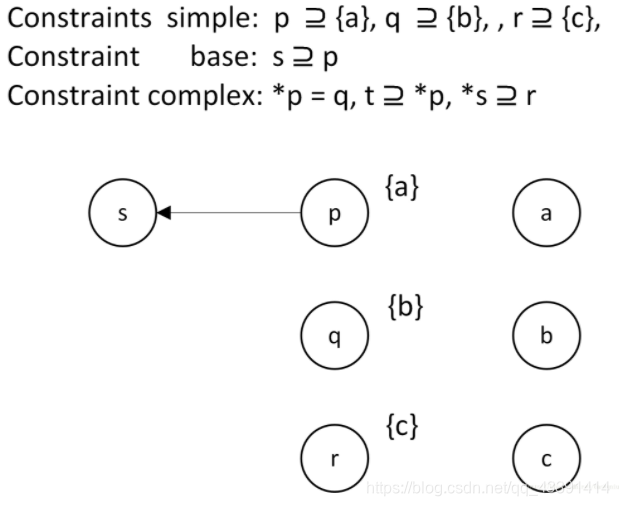
 解释：正如名字，上面只是约束图，而且只是一个初始约束图，图中的边也并不是指针的指向关系，而是约束关系。拿上图的边edge(p,s)为例，其表示p所指向的，s都将指向。

实战

下面用一个例子来进行实战整个Anderson算法。

int i, j, k;
int *a = &i;int *b = &k;a = &j;int *p = &a;int *q = &b;p = q;int *c = *q;

可以得到如下的约束：

   a ⊇ {i, j}, b ⊇ {k}, p ⊇ {a}, q ⊇ {b}, p ⊇ q, c ⊇ *q

从而得到如下初始约束图：

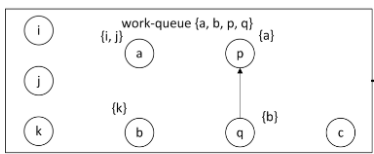
上面的work_queue工作队列就是下面伪代码中的W。伪代码如下：
（我们已经完成了1，2步了）。

 开始执行循环，从队列中取出a。
由于找不到关于a的复杂约束，复杂约束是什么？除了简单约束和基本约束就是复杂约束，具体可以参照开头的那个表格。
由于找不到a出发的边，所以此循环结束，如下。

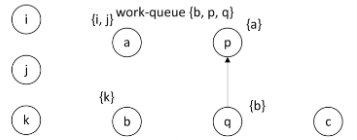
取出b,
找不到关于b的复杂约束
找不到b出发的边
此循环结束，如下。

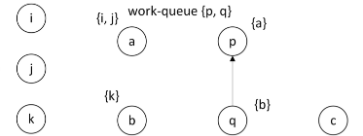
取出p，
找不到复杂约束
找不到p出发的边。
此循环结束，如下。

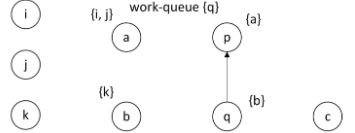
取出q,
找到复杂约束，c ⊇ *q。q的指向有b,从而加入边edge(b,c)。而且加入b到工作队列中。
找到q出发的边edge(q,p),所以pts§={a,b},由于pts§改变了，增加了一个元素，所以p再次加入到工作队列中。
此循环结束。

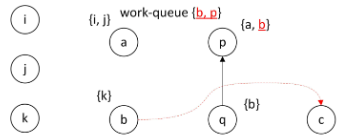
取出b,
没有复杂约束
找到b出发的边，所以pts©={k},由于pts©改变了，所以c加入到工作队列中。
此循环结束。

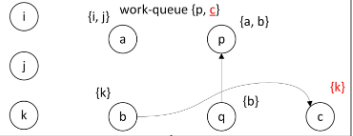
取出p,
没有复杂约束
没有从p出发的边
此循环结束。

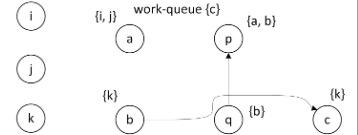
取出c,
找到复杂约束c ⊇ *q，但是复杂约束的形式和算法中的不一样，所以for循环结束。
找不到c出发的边
此循环结束。

由于工作队列为空，此算法结束。
将旁边的那些集合比如{i，j}统统连上，即edge(a,i),edge(a,j)…。就变成了我们最终要的指针指向关系了。

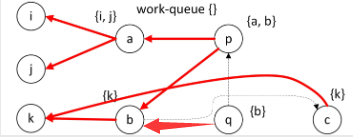
这样我们就完成了指针分析。