图的搜索算法---8.2 ZOJ1002-Fire Net--合理布置碉堡

目录

问题：

分析：

 主要的算法代码：

完整代码： 

出问题的代码：

原因：

正确代码：

代码分析：

运行结果：

问题：

¢ 假设我们有一个方形的城市，其街道都是直的。在方形地图上，有 n 行和 n 列，每个代表一条街道或一堵墙。每个碉堡有 4个射击孔，分别正对东西南北方向。在每个射击孔配备一架高射机枪。

¢ 我们假设，子弹是如此强大，它的射程可以任意远，并能摧毁它所击中的碉堡。墙也是很坚固的，足以阻止子弹的摧毁。

¢ 问题的目标是，在该城市中布置尽可能多的碉堡，而碉堡之间又不会相互摧毁。合理布置碉堡的原则是，没有两个碉堡在同一个水平方向或垂直方向，除非它们之间有墙相隔。在本题中，假定城市很小（最多 4 × 4），而且有子弹不能贯穿的墙壁。

分析：

（1）数据定义，读取数据

char cMap[5][5];  //地图

int iBest;  //最优解

int n;  //地图的大小

¢ 数据读取：

while(scanf("%d", &n) && n)

{ 

  for(int i = 0; i < n; i++)

        cin>>cMap[i];

  ……

}

 （2）判断每个单元格能否放置碉堡

 主要的算法代码：

/*算法8.1（1） 放置碉堡的深度优先搜索算法
*/
//回溯算法，子集树
void solve(int k, int current)
{　　int x, y;if(k == n*n) 　　//整个地图判断完毕{　　//更新最优解if(current > iBest){iBest = current; return;}}else{　//将单元数转换为xy坐标x = k / n;y = k % n;if(cMap[x][y] == ‘.’  &&  CanPut(x, y))	//左子树{cMap[x][y] = 'O';　　　	//放置一个碉堡solve(k + 1, current + 1);cMap[x][y] = ‘.’; 		//恢复现场}solve(k + 1, current);　		//不放置碉堡，右子树}
}/*算法8.1（2）判断在行row和列col处能否配置碉堡
*/bool CanPut(int row,  int col)
{　　int i;//判断col列上的合法性for(i = row - 1; i >= 0; i--){if(cMap[i][col] == 'O') return false;if(cMap[i][col] == 'X') break;}//判断row行上的合法性for(i = col - 1; i >= 0; i--){if(cMap[row][i] == 'O') return false;if(cMap[row][i] == 'X') break;}return true;
}

该算法使用深度优先搜索（DFS）的思想，从地图的左上角开始，尝试在每个单元格中放置碉堡或者不放置碉堡，直到整个地图都被覆盖。在 DFS 的过程中，我们通过 CanPut 函数来判断当前位置能否放置碉堡，通过 solve 函数进行递归搜索，最后更新最优解并输出。 

完整代码： 

出问题的代码：

• 无论输入什么，结果都为0.

/*
*	假设我们有一个方形的城市，其街道都是直的。在方形地图上，有n行和n列，每个代表一条街道或一堵墙。每个碉堡有4个射击孔，分别正对东西南北方向。在每个射击孔配备一架高射机枪。我们假设，子弹是如此强大，它的射程可以任意远，并能摧毁它所击中的碉堡。墙也是很坚固的，足以阻止子弹的摧毁。问题的目标是，在该城市中布置尽可能多的碉堡，而碉堡之间又不会相互摧毁。合理布置碉堡的原则是，没有两个碉堡在同一个水平方向或垂直方向，除非它们之间有墙相隔。在本题中，假定城市很小（最多4×4），而且有子弹不能贯穿的墙壁。
*/
#include<iostream>
using namespace std;char cMap[5][5];	//地图
int iBest;		   //最优解
int n;			  //地图大小//判断在行row和列col处能否配置碉堡
bool CanPut(int row, int col) {int i;//判断col列上的合法性for(i = row - 1; i >= 0; i++) {if (cMap[i][col] == 'O')return false;if (cMap[i][col] == 'X')break;}//判断row行上的合法性for (i = col - 1; i >= 0; i--) {if (cMap[row][i] == 'O')return false;if (cMap[row][i] == 'X')break;}return true;
}//放置碉堡的深度优先搜索算法
void solve(int k,int current) {int x, y;//整个地图判断完毕if (k = n * n) {if (current > iBest) {iBest = current;return;}}else{//将单元数转换为xy坐标x = k / n;//行y = k % n;//列//左子树if (cMap[x][y] == '.' && CanPut(x, y)) {//放置一个碉堡cMap[x][y] = 'O';solve(k + 1, current + 1);//恢复现场cMap[x][y] = '.';}solve(k + 1, current);//不放置碉堡，右子树}
}int main() {while (cin >> n && n) {for (int i = 0; i < n; i++) {cin >> cMap[i];}iBest = 0;//初始化最优解为0solve(0, 0);//从第一个单元格开始搜索cout << iBest << "\\t";//输出最优解cout << endl;}return 0;
}

原因：

这个代码存在一些问题：

1. 在 CanPut 函数中，第 5 行的循环条件错误，应该是 i >= 0 而不是 i++，否则会导致死循环。
2. 在 solve 函数中，第 17 行的判断条件使用了赋值符号 =，应该改为相等性判断符号 ==。
3. 在 solve 函数中，没有对地图进行 DFS 搜索时需要恢复现场，即放置/撤回碉堡，否则会影响后续的搜索结果。在放置碉堡后递归搜索后，需要在返回时立即撤回放置的碉堡，恢复现场，使得程序能够正确地搜索到剩余的节点。

修改后的代码如下所示：

//判断在行row和列col处能否配置碉堡
bool CanPut(int row, int col) {int i;//判断col列上的合法性for(i = row - 1; i >= 0; i--) {if (cMap[i][col] == 'O')return false;if (cMap[i][col] == 'X')break;}//判断row行上的合法性for (i = col - 1; i >= 0; i--) {if (cMap[row][i] == 'O')return false;if (cMap[row][i] == 'X')break;}return true;
}//放置碉堡的深度优先搜索算法
void solve(int k,int current) {int x, y;//整个地图判断完毕if (k == n * n) {if (current > iBest) {iBest = current;}return;  // 返回时需要恢复现场，即撤回放置的碉堡}else{//将单元数转换为xy坐标x = k / n;//行y = k % n;//列//左子树if (cMap[x][y] == '.' && CanPut(x, y)) {//放置一个碉堡cMap[x][y] = 'O';solve(k + 1, current + 1);//恢复现场cMap[x][y] = '.';}solve(k + 1, current);//不放置碉堡，右子树}
}int main() {while (cin >> n && n) {for (int i = 0; i < n; i++) {cin >> cMap[i];}iBest = 0;//初始化最优解为0solve(0, 0);//从第一个单元格开始搜索cout << iBest << "\\t";//输出最优解cout << endl;}return 0;
}

正确代码：

示例1-

#include<iostream>
using namespace std;const int MAXN = 4;
char cMap[MAXN][MAXN];//地图
int iBest;//最优解
int n;//地图大小//判断在行row和列col处能否配置碉堡
bool CanPut(int row, int col) {int i;//判断col列上的合法性for (i = row - 1; i >= 0; i--) {if (cMap[i][col] == 'O')return false;if (cMap[i][col] == 'X')break;}for (i = row + 1; i < n; i++) {if (cMap[i][col] == 'O')return false;if (cMap[i][col] == 'X')break;}//判断row行上的合法性for (i = col - 1; i >= 0; i--) {if (cMap[row][i] == 'O')return false;if (cMap[row][i] == 'X')break;}for (i = col + 1; i < n; i++) {if (cMap[row][i] == 'O')return false;if (cMap[row][i] == 'X')break;}return true;
}//放置碉堡的深度优先搜索算法
void solve(int k, int current) {int x, y;//整个地图判断完毕if (k == n * n) {if (current > iBest) {iBest = current;return;}}else {//将单元数转换为xy坐标x = k / n;//行y = k % n;//列//左子树if (cMap[x][y] == '.' && CanPut(x, y)) {//放置一个碉堡cMap[x][y] = 'O';solve(k + 1, current + 1);//恢复现场cMap[x][y] = '.';}solve(k + 1, current);//不放置碉堡，右子树}
}int main() {while (cin >> n && n) {for (int i = 0; i < n; i++) {cin >> cMap[i];}iBest = 0;//最优解初始化为0solve(0, 0);//从第一个单元格开始搜索cout << iBest << endl;//输出最优解}return 0;
}

示例2--

 【针对错误修改后的】

/*
*	假设我们有一个方形的城市，其街道都是直的。在方形地图上，有n行和n列，每个代表一条街道或一堵墙。每个碉堡有4个射击孔，分别正对东西南北方向。在每个射击孔配备一架高射机枪。我们假设，子弹是如此强大，它的射程可以任意远，并能摧毁它所击中的碉堡。墙也是很坚固的，足以阻止子弹的摧毁。问题的目标是，在该城市中布置尽可能多的碉堡，而碉堡之间又不会相互摧毁。合理布置碉堡的原则是，没有两个碉堡在同一个水平方向或垂直方向，除非它们之间有墙相隔。在本题中，假定城市很小（最多4×4），而且有子弹不能贯穿的墙壁。
*/
#include<iostream>
using namespace std;char cMap[5][5];	//地图
int iBest;		   //最优解
int n;			  //地图大小//判断在行row和列col处能否配置碉堡
bool CanPut(int row, int col) {int i;//判断col列上的合法性for (i = row - 1; i >= 0; i--) {if (cMap[i][col] == 'O')return false;if (cMap[i][col] == 'X')break;}//判断row行上的合法性for (i = col - 1; i >= 0; i--) {if (cMap[row][i] == 'O')return false;if (cMap[row][i] == 'X')break;}return true;
}//放置碉堡的深度优先搜索算法
void solve(int k, int current) {int x, y;//整个地图判断完毕if (k == n * n) {if (current > iBest) {iBest = current;return;}}else {//将单元数转换为xy坐标x = k / n;//行y = k % n;//列//左子树if (cMap[x][y] == '.' && CanPut(x, y)) {//放置一个碉堡cMap[x][y] = 'O';solve(k + 1, current + 1);//恢复现场cMap[x][y] = '.';}solve(k + 1, current);//不放置碉堡，右子树}
}int main() {while (cin >> n && n) {for (int i = 0; i < n; i++) {cin >> cMap[i];}iBest = 0;//初始化最优解为0solve(0, 0);//从第一个单元格开始搜索cout << iBest;//输出最优解cout << endl;}return 0;
}

代码分析：

【示例2--】这段代码实现了一个基于深度优先搜索（DFS）的算法来解决布置碉堡的问题。在地图上放置碉堡时，需要保证每个碉堡之间不能相互摧毁，即两个碉堡不能在同一行或同一列，除非它们之间被隔开的是墙。

      具体地，算法的主要思路是，采用 DFS 算法的思想，从第一个单元格开始逐个位置进行判断，如果该位置可以放置碉堡，则将其放置，并以此为基础继续向下搜索；如果该位置不能放置碉堡，则不做处理并继续向下搜索。搜索过程中需要记录当前已经放置的碉堡的数量，当所有空位都被判断完毕时，将当前数量与历史最佳数量比较，更新最佳数量即可。同时，       

      在放置碉堡后，需要及时恢复现场，即撤回放置的碉堡，使得程序能够正确地搜索到剩余的节点。

总之，该算法通过深度优先搜索实现了对于布置碉堡的问题的求解，从而找到在给定地图内布置尽可能多的碉堡的方案。

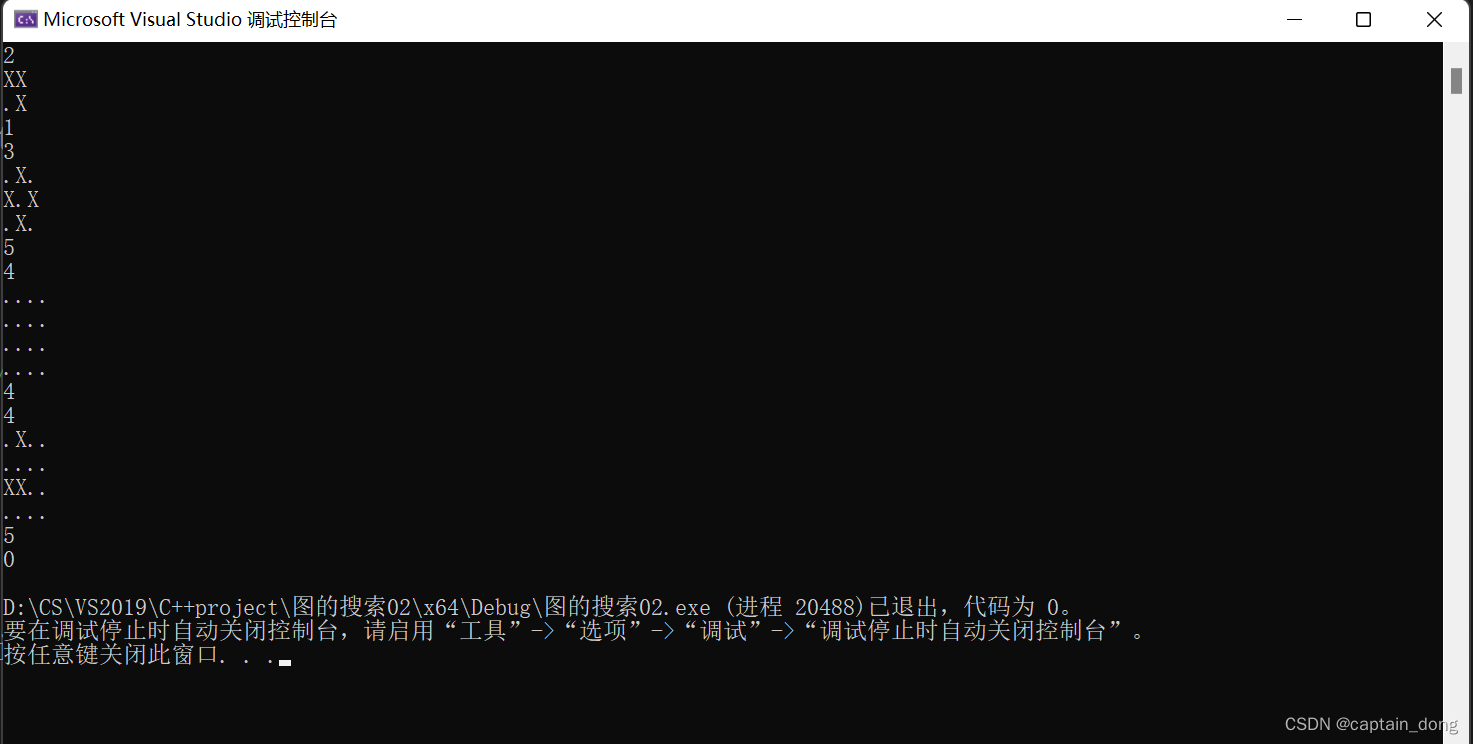
运行结果：

1--

2---