⚠申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计8149字，阅读大概需要3分钟
🌈更多学习内容， 欢迎👏关注👀【文末】我的个人微信公众号：不懂开发的程序猿
个人网站：https://jerry-jy.co/

经典图论算法

并查集算法

并查集（Union-Find）是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。

并查集的思想是用一个数组表示了整片森林（parent），树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里。

动态连通性

简单说，动态连通性其实可以抽象成给一幅图连线。比如下面这幅图，总共有 10 个节点，他们互不相连，分别用 0~9 标记：

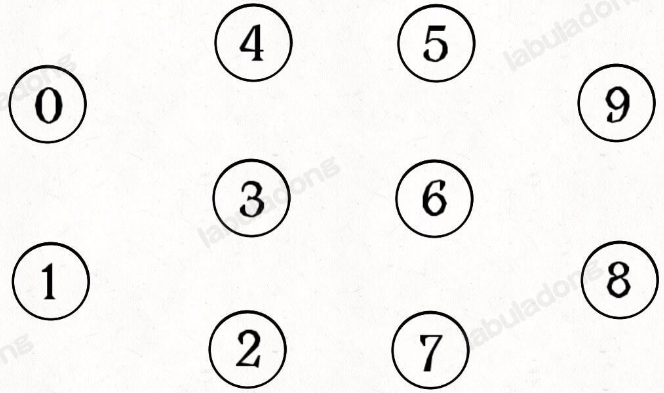
现在我们的 Union-Find 算法主要需要实现这两个 API：

class UF {/* 将 p 和 q 连接 */public void union(int p, int q);/* 判断 p 和 q 是否连通 */public boolean connected(int p, int q);/* 返回图中有多少个连通分量 */public int count();
}

这里所说的「连通」是一种等价关系，也就是说具有如下三个性质：

1、自反性：节点 p 和 p 是连通的。

2、对称性：如果节点 p 和 q 连通，那么 q 和 p 也连通。

3、传递性：如果节点 p 和 q 连通，q 和 r 连通，那么 p 和 r 也连通。

比如说之前那幅图，0～9 任意两个不同的点都不连通，调用 connected 都会返回 false，连通分量为 10 个。

如果现在调用 union(0, 1)，那么 0 和 1 被连通，连通分量降为 9 个。

再调用 union(1, 2)，这时 0,1,2 都被连通，调用 connected(0, 2) 也会返回 true，连通分量变为 8 个

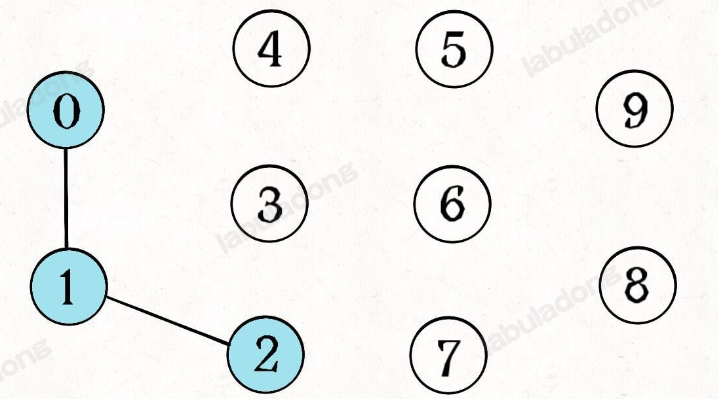
思路

怎么用森林来表示连通性呢？我们设定树的每个节点有一个指针指向其父节点，如果是根节点的话，这个指针指向自己。比如说刚才那幅 10 个节点的图，一开始的时候没有相互连通，就是这样：

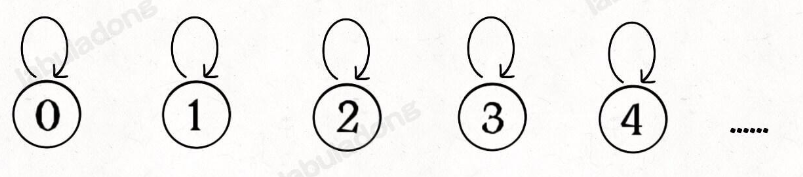
class UF {// 记录连通分量private int count;// 节点 x 的父节点是 parent[x]private int[] parent;/* 构造函数，n 为图的节点总数 */public UF(int n) {// 一开始互不连通this.count = n;// 父节点指针初始指向自己parent = new int[n];for (int i = 0; i < n; i++)parent[i] = i;}/* 其他函数 */
}

如果某两个节点被连通，则让其中的（任意）一个节点的根节点接到另一个节点的根节点上：

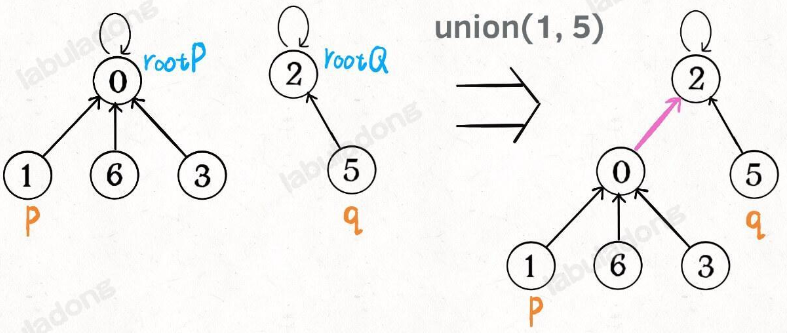
class UF {// 省略上文给出的代码部分...public void union(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;// 将两棵树合并为一棵parent[rootP] = rootQ;// parent[rootQ] = rootP 也一样count--; // 两个分量合二为一}/* 返回某个节点 x 的根节点 */private int find(int x) {// 根节点的 parent[x] == xwhile (parent[x] != x)x = parent[x];return x;}/* 返回当前的连通分量个数 */public int count() { return count;}
}

这样，如果节点 p 和 q 连通的话，它们一定拥有相同的根节点：

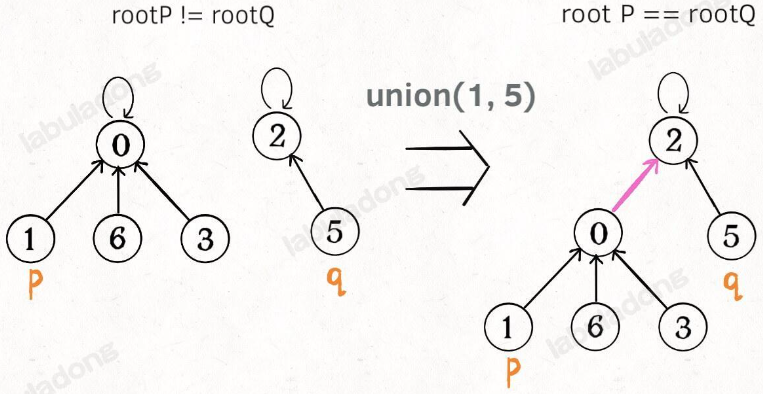
class UF {// 为了节约篇幅，省略上文给出的代码部分...public boolean connected(int p, int q) {int rootP = find(p);int rootQ = find(q);return rootP == rootQ;}
}

那么这个算法的复杂度是多少呢？我们发现，主要 API connected 和 union 中的复杂度都是 find 函数造成的，所以说它们的复杂度和 find 一样。

find 主要功能就是从某个节点向上遍历到树根，其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是 logN，但这并不一定。logN 的高度只存在于平衡二叉树，对于一般的树可能出现极端不平衡的情况，使得「树」几乎退化成「链表」，树的高度最坏情况下可能变成 N。

平衡性优化

树的不平衡现象，关键在于 union 过程

我们一开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面，那么这里就可能出现「头重脚轻」的不平衡状况，比如下面这种局面：

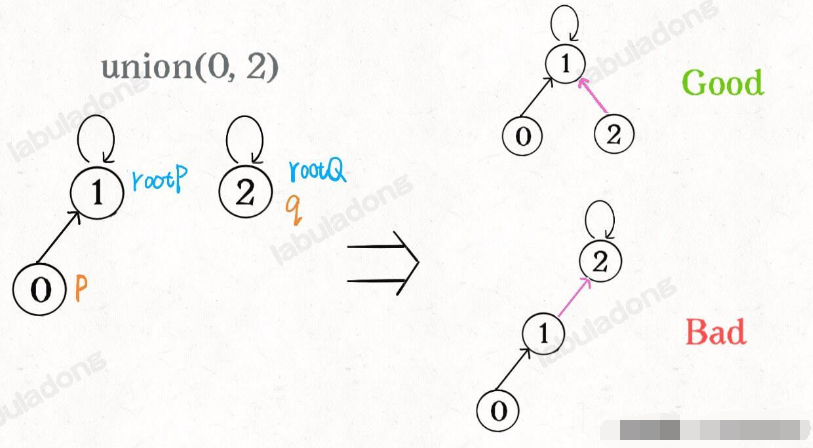
我们其实是希望，小一些的树接到大一些的树下面，这样就能避免头重脚轻，更平衡一些。解决方法是额外使用一个 size 数组，记录每棵树包含的节点数，我们不妨称为「重量」：

修改初始化

class UF {private int count;private int[] parent;// 新增一个数组记录树的“重量”private int[] size;public UF(int n) {this.count = n;parent = new int[n];// 最初每棵树只有一个节点// 重量应该初始化 1size = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;size[i] = 1;}}/* 其他函数 */
}

修改union( )函数

class UF {// 为了节约篇幅，省略上文给出的代码部分...public void union(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;// 小树接到大树下面，较平衡if (size[rootP] > size[rootQ]) {parent[rootQ] = rootP;size[rootP] += size[rootQ];} else {parent[rootP] = rootQ;size[rootQ] += size[rootP];}count--;}
}

树的高度大致在 logN 这个数量级，极大提升执行效率。

路径压缩

其实我们并不在乎每棵树的结构长什么样，只在乎根节点。

因为无论树长啥样，树上的每个节点的根节点都是相同的，所以能不能进一步压缩每棵树的高度，使树高始终保持为常数？

这样每个节点的父节点就是整棵树的根节点，find 就能以 O(1) 的时间找到某一节点的根节点，相应的，connected 和 union 复杂度都下降为 O(1)。

要做到这一点主要是修改 find 函数逻辑

第一种是在 find 中加一行代码：

class UF {// 为了节约篇幅，省略上文给出的代码部分...private int find(int x) {while (parent[x] != x) {// 这行代码进行路径压缩parent[x] = parent[parent[x]];x = parent[x];}return x;}
}

每次 while 循环都会把一对儿父子节点改到同一层，这样每次调用 find 函数向树根遍历的同时，顺手就将树高缩短了

路径压缩的第二种写法是这样：

class UF {// 为了节约篇幅，省略上文给出的代码部分...// 第二种路径压缩的 find 方法public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}
}

这种路径压缩的效果如下：

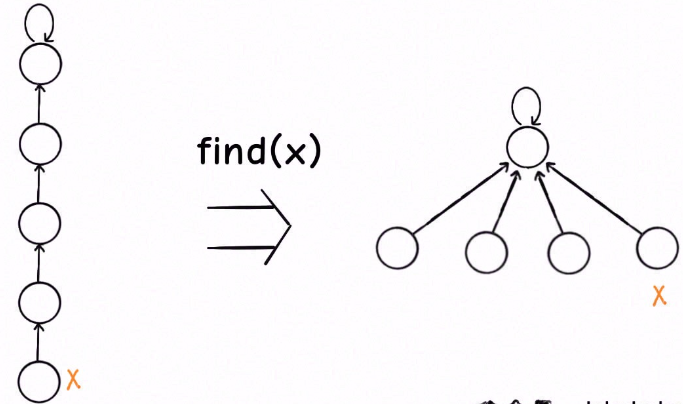
另外，如果使用路径压缩技巧，那么 size 数组的平衡优化就不是特别必要了。

一般看到的 Union Find 算法应该是如下实现：

Union Find 算法

class UF {// 连通分量个数private int count;// 存储每个节点的父节点private int[] parent;// n 为图中节点的个数public UF(int n) {this.count = n;parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}}// 将节点 p 和节点 q 连通public void union(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;parent[rootQ] = rootP;// 两个连通分量合并成一个连通分量count--;}// 判断节点 p 和节点 q 是否连通public boolean connected(int p, int q) {int rootP = find(p);int rootQ = find(q);return rootP == rootQ;}public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}// 返回图中的连通分量个数public int count() {return count;}
}

总结一下我们优化算法的过程：

1、用 parent 数组记录每个节点的父节点，相当于指向父节点的指针，所以 parent 数组内实际存储着一个森林（若干棵多叉树）。

2、用 size 数组记录着每棵树的重量，目的是让 union 后树依然拥有平衡性，保证各个 API 时间复杂度为 O(logN)，而不会退化成链表影响操作效率。

3、在 find 函数中进行路径压缩，保证任意树的高度保持在常数，使得各个 API 时间复杂度为 O(1)。使用了路径压缩之后，可以不使用 size 数组的平衡优化。

130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

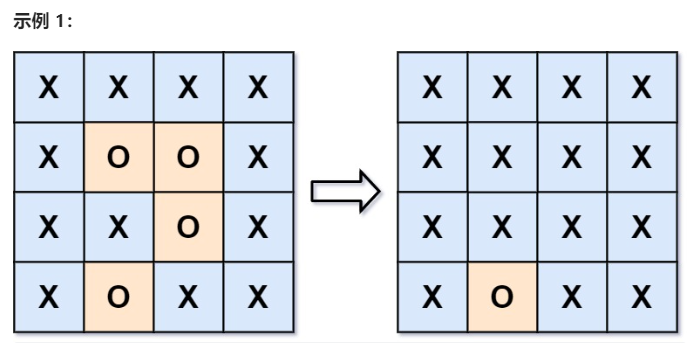
类似棋类游戏「黑白棋」，只要你用两个棋子把对方的棋子夹在中间，对方的子就被替换成你的子。可见，占据四角的棋子是无敌的，与其相连的边棋子也是无敌的（无法被夹掉）。

可以用DFS解决

这里采用 Union-Find 算法解决

你可以把那些不需要被替换的 O 看成一个拥有独门绝技的门派，它们有一个共同「祖师爷」叫 dummy，这些 O 和 dummy 互相连通，而那些需要被替换的 O 与 dummy 不连通。

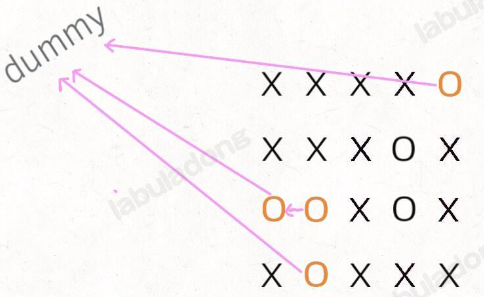
根据我们的实现，Union-Find 底层用的是一维数组，构造函数需要传入这个数组的大小，而题目给的是一个二维棋盘。

这个很简单，二维坐标 (x,y) 可以转换成 x * n + y 这个数（m 是棋盘的行数，n 是棋盘的列数），敲黑板，这是将二维坐标映射到一维的常用技巧。

其次，我们之前描述的「祖师爷」是虚构的，需要给他老人家留个位置。索引 [0.. m*n-1] 都是棋盘内坐标的一维映射，那就让这个虚拟的 dummy 节点占据索引 m * n 好了。

class Solution {public void solve(char[][] board) {if (board.length == 0) return;int m = board.length;int n = board[0].length;// 给 dummy 留一个额外位置UF uf = new UF(m * n + 1);int dummy = m * n;// 将首列和末列的 O 与 dummy 连通for (int i = 0; i < m; i++) {if (board[i][0] == 'O')uf.union(i * n, dummy);if (board[i][n - 1] == 'O')uf.union(i * n + n - 1, dummy);}// 将首行和末行的 O 与 dummy 连通for (int j = 0; j < n; j++) {if (board[0][j] == 'O')uf.union(j, dummy);if (board[m - 1][j] == 'O')uf.union(n * (m - 1) + j, dummy);}// 方向数组 d 是上下左右搜索的常用手法int[][] d = new int[][]{{1,0}, {0,1}, {0,-1}, {-1,0}};for (int i = 1; i < m - 1; i++) for (int j = 1; j < n - 1; j++) if (board[i][j] == 'O')// 将此 O 与上下左右的 O 连通for (int k = 0; k < 4; k++) {int x = i + d[k][0];int y = j + d[k][1];if (board[x][y] == 'O')uf.union(x * n + y, i * n + j);}// 所有不和 dummy 连通的 O，都要被替换for (int i = 1; i < m - 1; i++) for (int j = 1; j < n - 1; j++) if (!uf.connected(dummy, i * n + j))board[i][j] = 'X';}}class UF {// 连通分量个数private int count;// 存储每个节点的父节点private int[] parent;// n 为图中节点的个数public UF(int n) {this.count = n;parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}}// 将节点 p 和节点 q 连通public void union(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;parent[rootQ] = rootP;// 两个连通分量合并成一个连通分量count--;}// 判断节点 p 和节点 q 是否连通public boolean connected(int p, int q) {int rootP = find(p);int rootQ = find(q);return rootP == rootQ;}public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}// 返回图中的连通分量个数public int count() {return count;}
}

其实用 Union-Find 算法解决这个简单的问题有点杀鸡用牛刀，它可以解决更复杂，更具有技巧性的问题，主要思路是适时增加虚拟节点，想办法让元素「分门别类」，建立动态连通关系。

990. 等式方程的可满足性

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一："a==b" 或 "a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

核心思想是，将 equations 中的算式根据 == 和 != 分成两部分，先处理 == 算式，使得他们通过相等关系各自勾结成门派（连通分量）；然后处理 != 算式，检查不等关系是否破坏了相等关系的连通性。

class Solution {public boolean equationsPossible(String[] equations) {// 26 个英文字母UF uf = new UF(26);// 先让相等的字母形成连通分量for (String eq : equations) {if (eq.charAt(1) == '=') {char x = eq.charAt(0);char y = eq.charAt(3);uf.union(x - 'a', y - 'a');}}// 检查不等关系是否打破相等关系的连通性for (String eq : equations) {if (eq.charAt(1) == '!') {char x = eq.charAt(0);char y = eq.charAt(3);// 如果相等关系成立，就是逻辑冲突if (uf.connected(x - 'a', y - 'a'))return false;}}return true;}
}
class UF {// 连通分量个数private int count;// 存储每个节点的父节点private int[] parent;// n 为图中节点的个数public UF(int n) {this.count = n;parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}}// 将节点 p 和节点 q 连通public void union(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;parent[rootQ] = rootP;// 两个连通分量合并成一个连通分量count--;}// 判断节点 p 和节点 q 是否连通public boolean connected(int p, int q) {int rootP = find(p);int rootQ = find(q);return rootP == rootQ;}public int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}// 返回图中的连通分量个数public int count() {return count;}
}

–end–