技术干货 | 基于Modelica的ANCF绳索建模与应用

绳索在我们日常生活中司空见惯,小到我们每天都会使用到的升降电梯,大到卫星上的大型可展开天线、捕获太空垃圾的绳网,都有它的身影。绳索与滑轮组合使用后又能形成一套传动系统,如起重设备、皮带轮系统等,能够长距离地传递平行轴或者任意轴之间的旋转和直线运动。

△ 绳网捕获太空垃圾示意图
那么像绳索这样的柔性体怎么搭建它的动力学模型呢?从机理上看,这涉及到多体动力学、刚柔耦合动力学及接触力学。接下来,笔者将介绍如何基于Modelica语言,使用系统建模仿真环境MWORKS.Sysplorer搭建由绳索和滑轮组成的传动系统的动力学模型。本文关注的重点是基于ANCF(Absolute Nodal Coordinate Formulation,绝对节点坐标公式)理论的柔性绳索实现过程。

1.1 有限单元法
一般在柔性体的建模中都会使用到有限单元法。在有限单元法中,绳索被划分为若干段(单元),段与段之间通过节点连接。通过计算出各节点处的位移矢量,绳索上任意一个物质点的位置都能由形状函数插值得到。本文使用到的是基于有限单元法的ANCF绳索单元。
1.2 刚柔耦合动力学
刚柔耦合系统是指由刚体和柔性体通过不同的连接方式构成的复杂动力学系统,是刚体动力学的延申内容。它主要研究柔性体的变形与其大范围空间运动之间的耦合。本文通过拉格朗日乘子法实现绳索(柔性体)与提拉物体(刚体)的位置约束。
1.3 接触力学
绳索与滑轮的接触力建模是影响绳索动态行为的关键因素。通常刚体间的接触满足以下三个条件:1.刚体之间不产生明显穿透;2.刚体之间能够传递法向压力和切向摩檫力;3.刚体之间不传递法向拉力。本文在法向接触力上使用非线性阻尼模型,在切向摩檫力上使用Hollars模型,通过罚函数法实现绳索与滑轮之间的不穿透约束。

滑轮绳索模型的构建主要分为以下三个步骤:
(1)绳索单元的划分和组装;
(2)通过拉格朗日乘子法施加位置约束,实现柔性绳索与刚体的连接;
(3)通过罚函数法建立绳索与滑轮的接触。
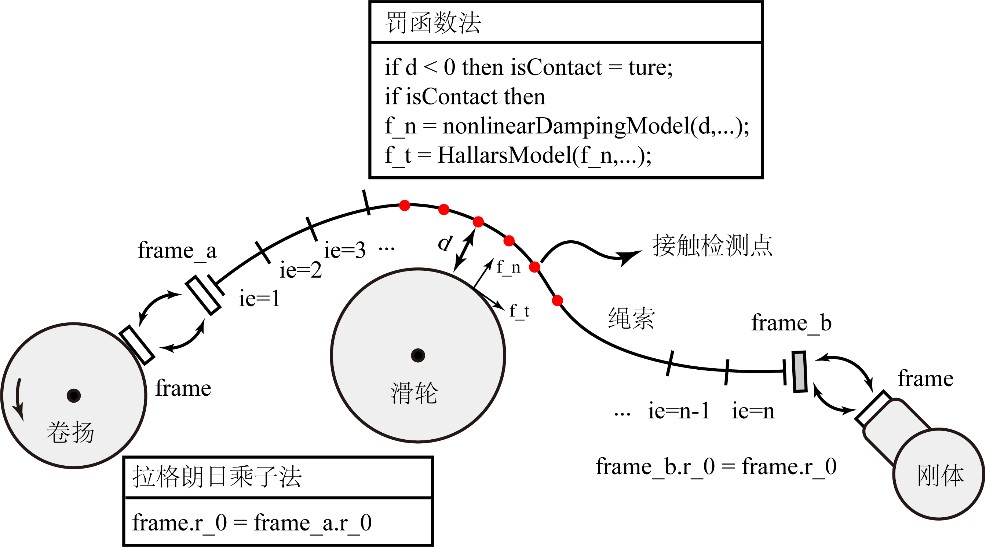
△ 建模流程示意图
2.1 绳索模型构建
在绝对节点坐标公式中,绳索单元定义在惯性坐标系下,单元的节点坐标使用全局位移和斜率描述。以二维平面绳索单元为例,如下图所示,该单元的节点坐标矢量可以表示为:
其中,,
,
,
是节点的全局位移;
,
,
,
是节点的全局斜率。
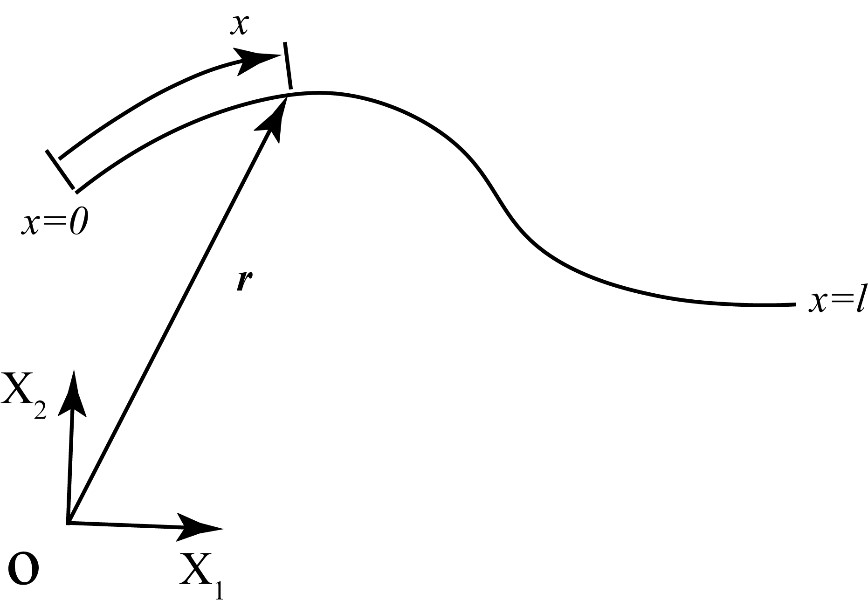
△ ANCF绳索单元
单元上任意一点的位置可以由节点坐标矢量插值得到,有如下表达式:
其中 为形状函数矩阵,可以写做如下:
矩阵内元素定义如下:
,
,
,
,其中
。
应用虚功原理可以得到单元的动力学方程有如下矩阵形式:
其中,是单元的质量矩阵,
是单元的弹性力矢量,
是单元的外力矢量,分别有如下表达式:
式中,,
。
可以分成集中力和分布力,有如下表达式:
其中,为集中力的作用点位置,
为集中力矢量,
为与位置有关的分布力函数。
有了以上公式我们就可以利用Modelica语言编写有限元程序了,由于篇幅限制,编程的细节不再赘述,在这里只提几点笔者使用Modelica语言编写有限元程序的经验:
(1)在矩阵组装时根据Modelica的语言特性,我们需要在数组元素赋值前声明好元素个数,数组元素赋值时通过两层for循环给二维数组中的元素一一赋值;
(2)由于Modelica语言是基于方程的编程语言,拥有强大的符号处理能力,只要方程的形式给出,内核可以方便地求出ODE和DAE问题的解,因此在使用Modelica进行有限元编程时我们要摒弃传统的过程式编程语言的编程范式,例如Modelica的function的输入可以是待求的状态变量,别小瞧了这点,这个特性能够让我们轻松的写出离散后的柔性体的动力学方程;
(3)同样基于第二点中描述的Modelica语言的特点,我们在完成柔性体的空间离散后,并不需要对时间域进行离散,这意味着我们并不需要手写时间积分算法,把一切交给强大的内核吧!
使用以下两个算例验证理论和程序编写的正确性。算例一问题设置为左端固支,右端自由的柔性绳索,自由端施加一集中力矩,力矩大小设置为,其中
,
为绳索的弹性模量,
为绳索的截面惯性矩,
为绳索的长度。根据文献[1],绳索在这一力矩作用下最终稳定成一个半圆形。
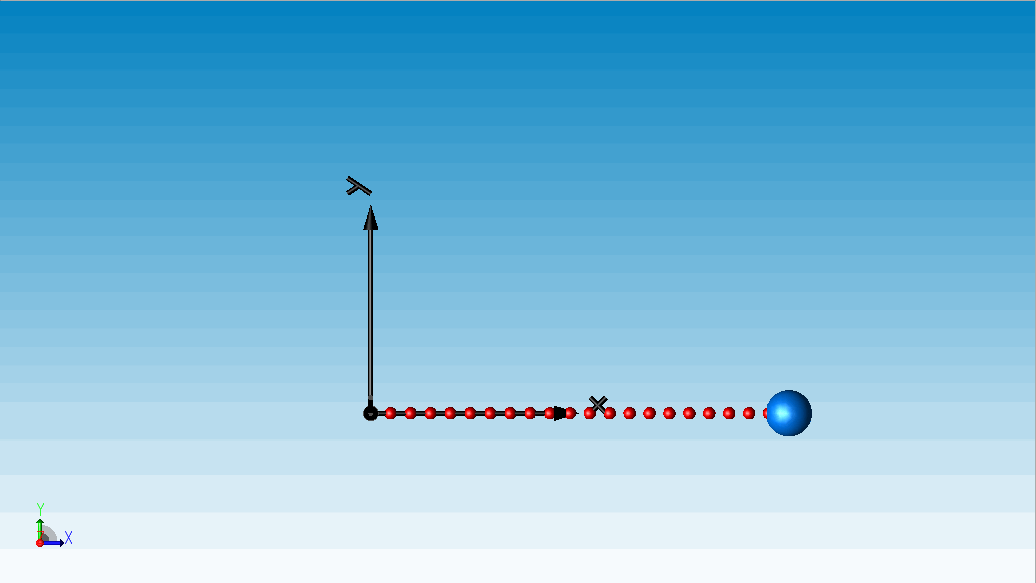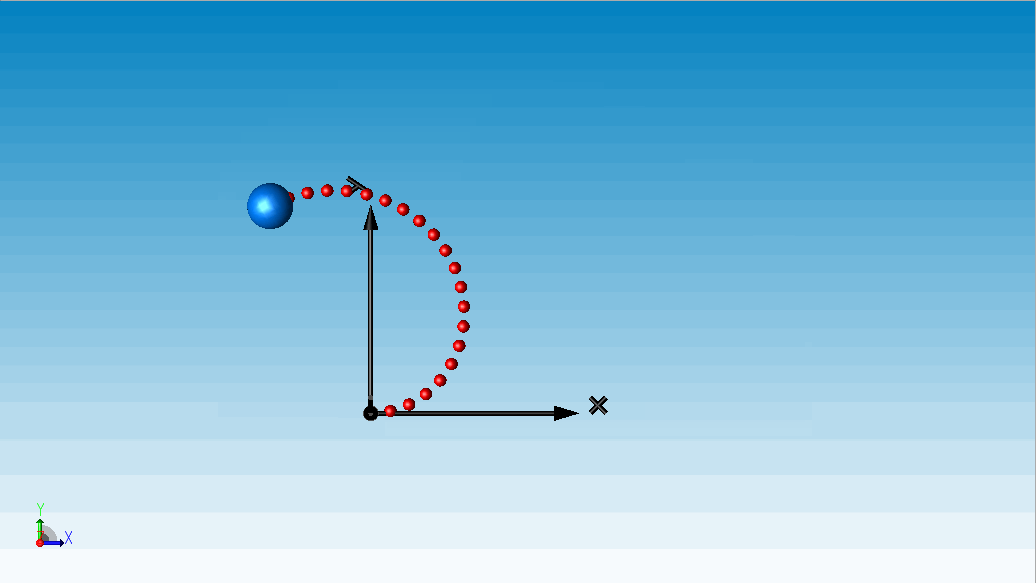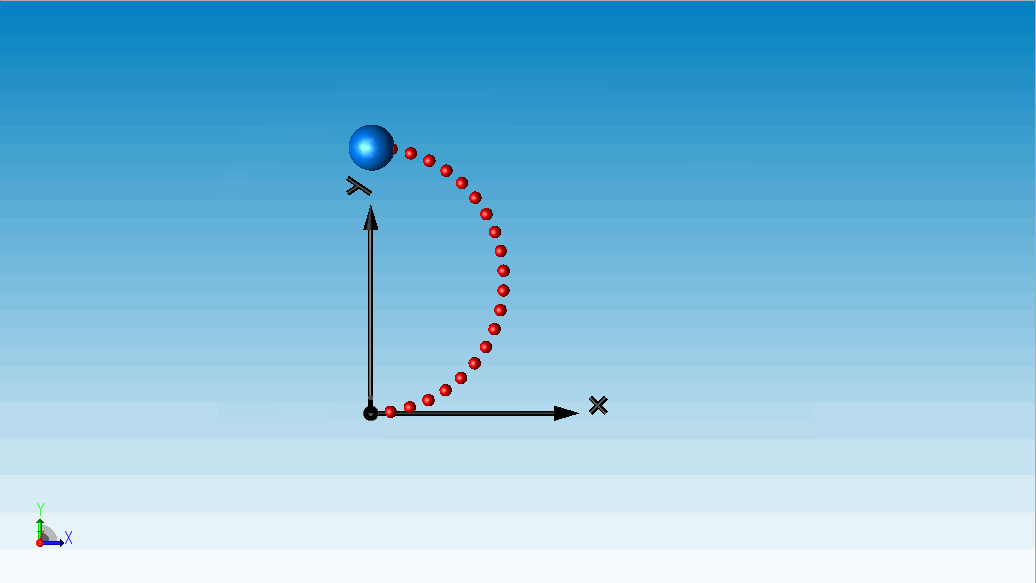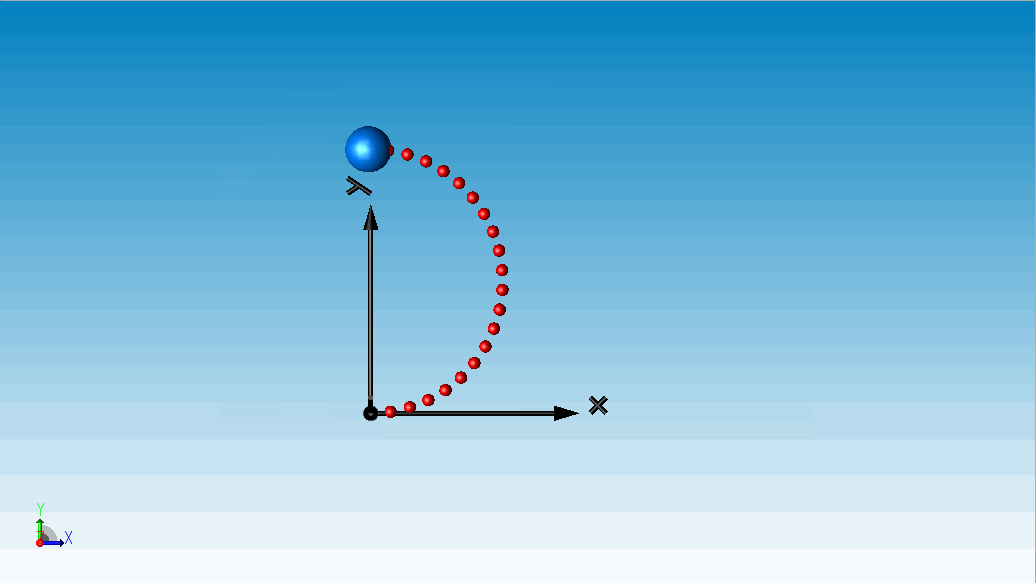
△ 算例一:柔性绳索弯曲成圆试验
算例二问题设置为一端铰接,一端自由的绳索,初始构型沿X轴正方向,初始角速度沿Y轴正方向,大小为4rad/s,重力方向设置为-Y方向。绳索的几何和材料参数如下:绳长1米,截面面积m^2,弹性模量
Pa,密度
kg/m^3,其中
。计算结果与文献[2]对比如下,可以发现在MWORKS上搭建的绳索模型和文献结果吻合很好。
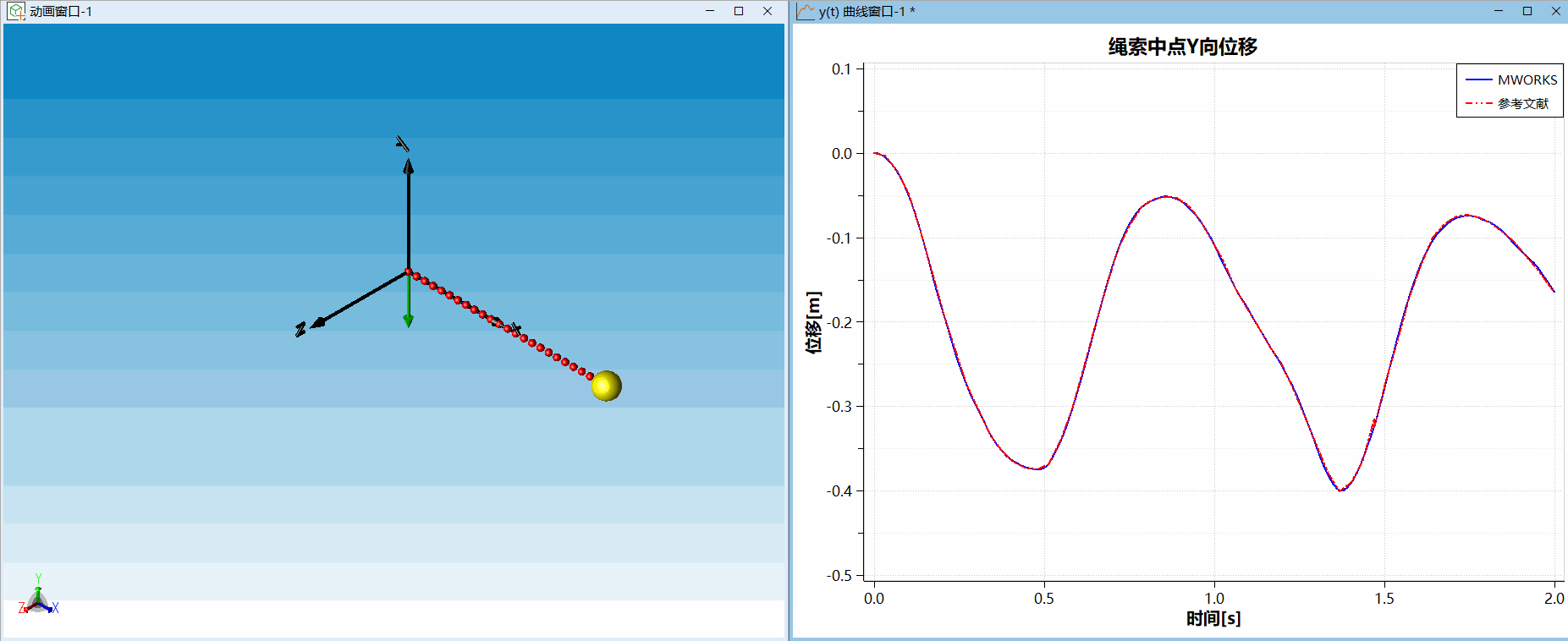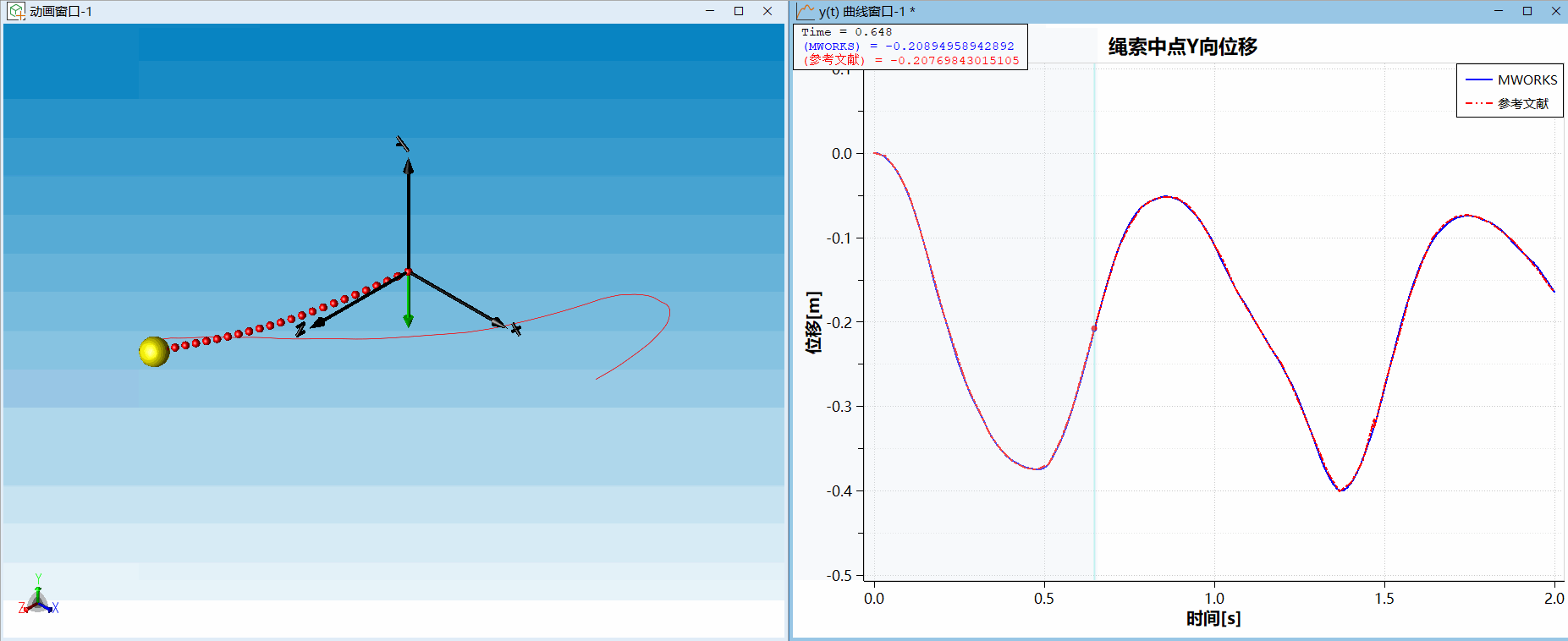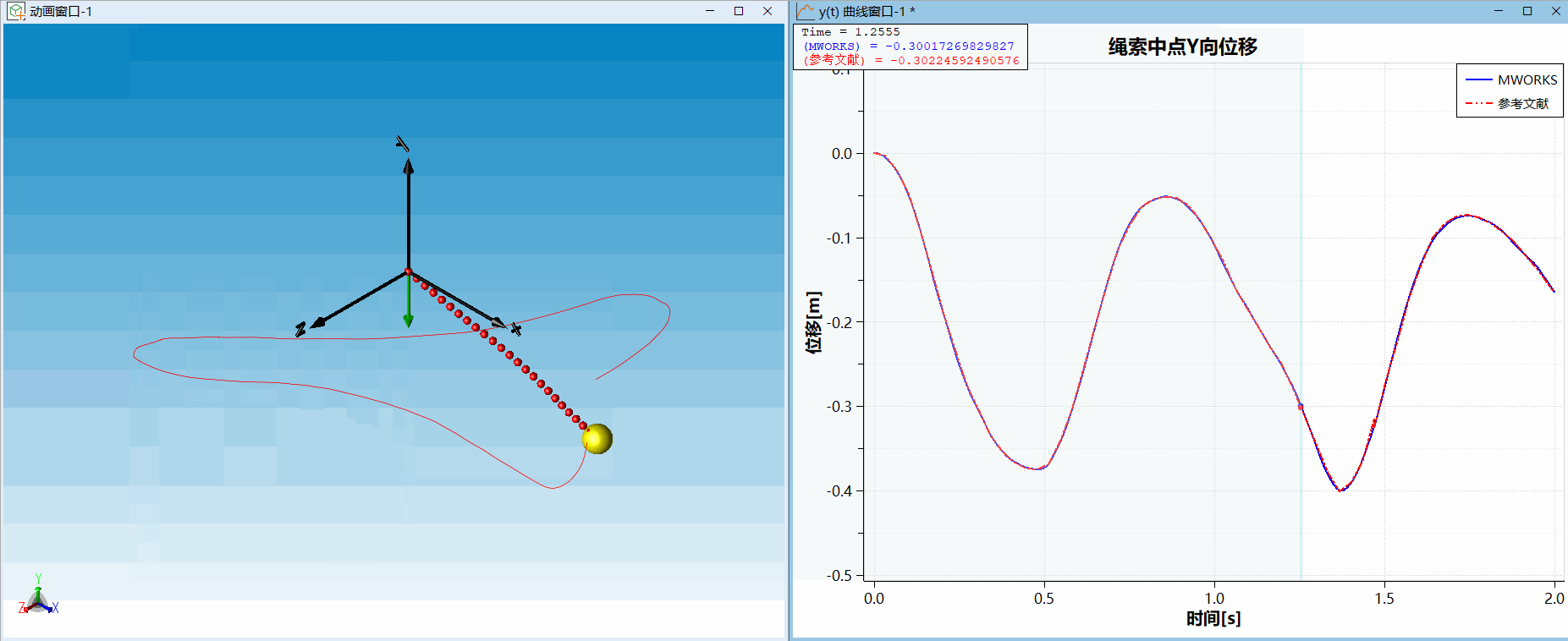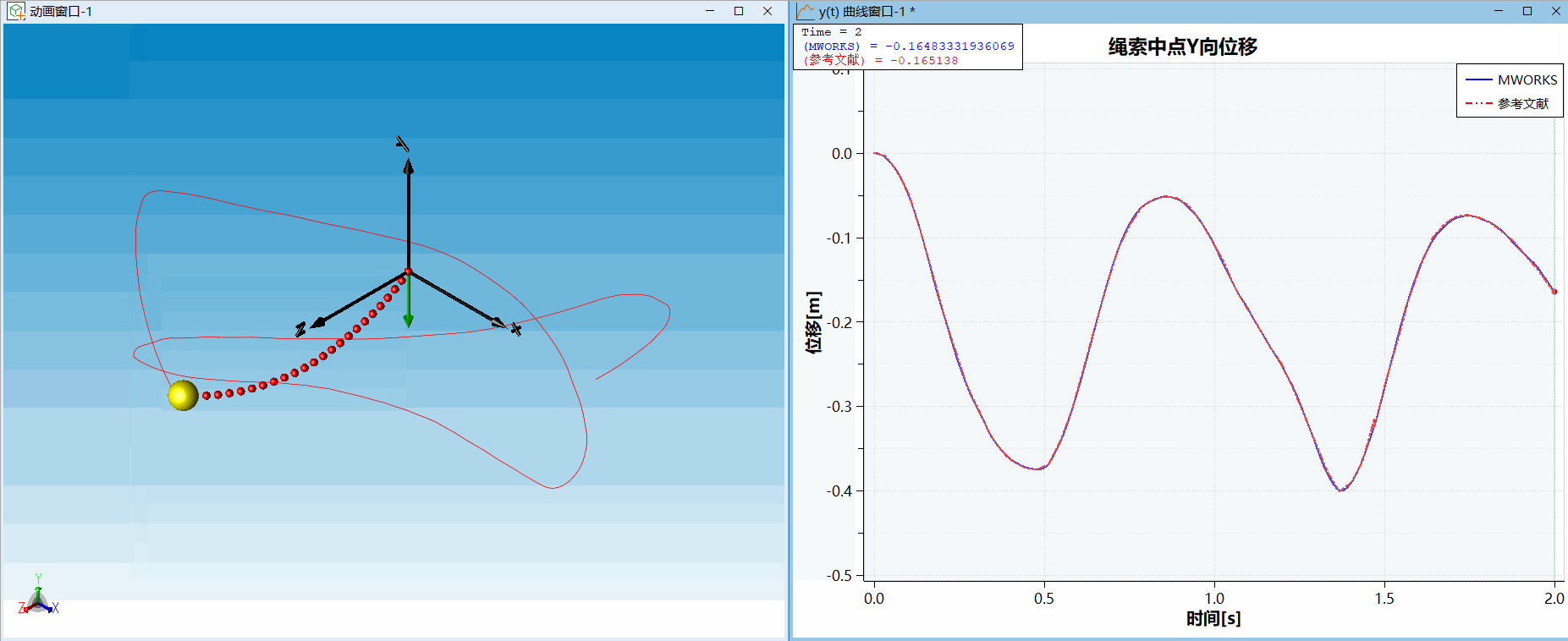
△ 算例二:三维绳摆试验
2.2 绳索刚柔耦合模型构建
有了单根绳索之后其实并不能解决工程上遇到的问题,因为大多数传动系统是由刚体和柔性体组合而成的,那么怎们实现柔性绳索与刚体之间的联动呢?在这里我们使用了Modelica标准库中的多体库来描述刚体运动,通过使用统一的Frame接口实现刚柔耦合分析。刚体和柔性体相连接的地方使用拉格朗日乘子法施加位置约束。下面展示的是使用绳索传动的曲柄滑块机构,让我们来看看效果吧!
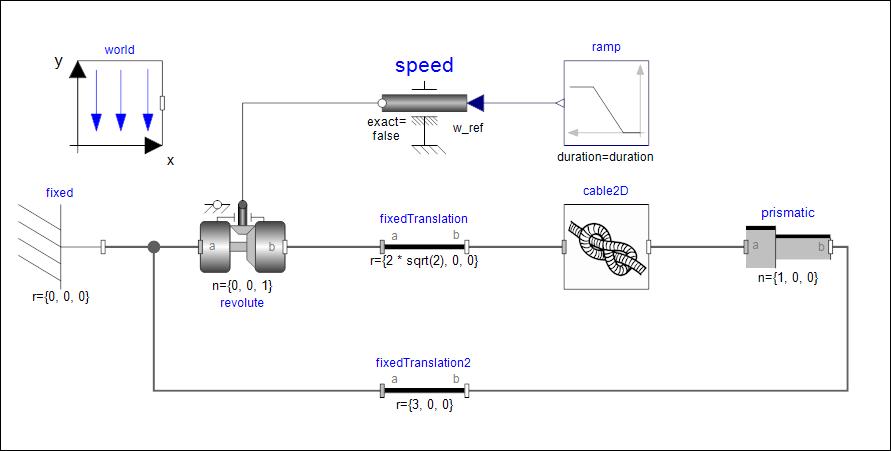
△ Modelica系统模型
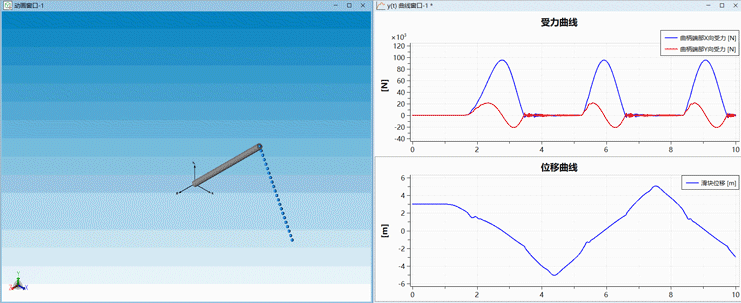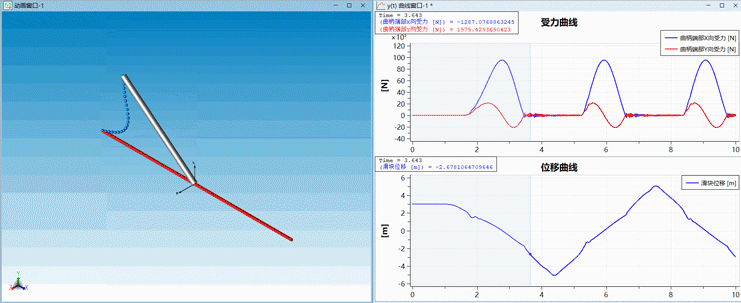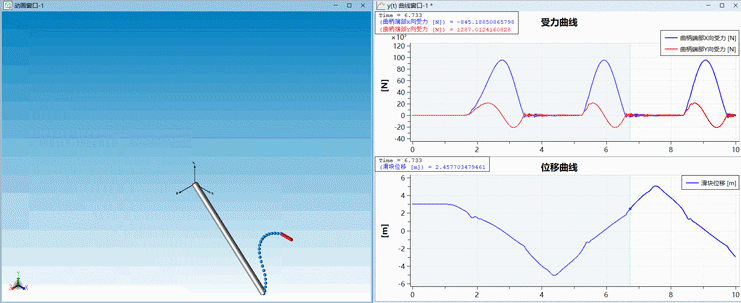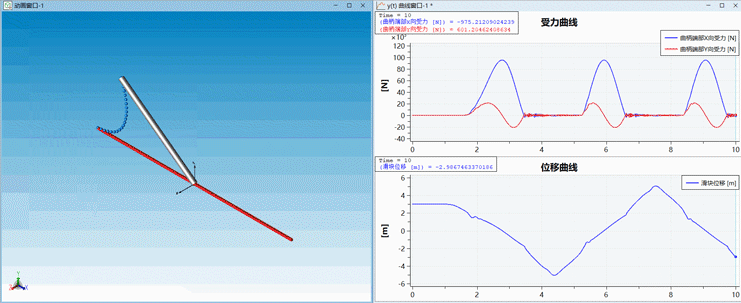
△ 动画效果
2.3 滑轮和卷扬模型构建
滑轮和卷扬是绳索传动系统中必不可少的组成部分,利用接触动力学的原理建立滑轮/卷扬与绳索之间的接触力就可以轻松实现绳索与滑轮/卷扬的组合。滑轮与绳索之间的法向接触力建模为非线性阻尼模型,有如下公式描述:
其中,表示接触刚度,
表示接触阻尼,
表示互相接触的两物体间的穿透深度,
为与接触物体形状和材料相关的系数。
滑轮与绳索之间的切向摩檫力使用Hollars模型,有如下公式描述:
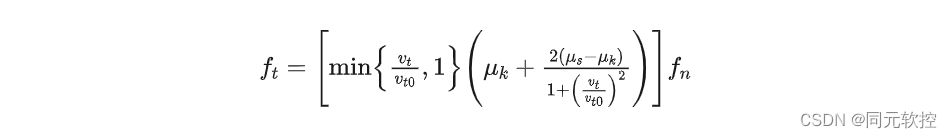
其中,为碰撞的两个物体的相对速度,
为由静摩擦转变为动摩擦的速度阈值,
为法向接触力,
和
分别为静摩擦系数和动摩擦系数。利用新构建的滑轮和卷扬我们搭建了一个简单的起重系统,一起来看看效果吧!
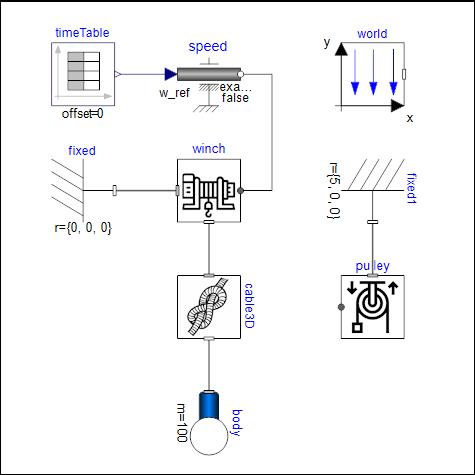
△ Modelica系统模型
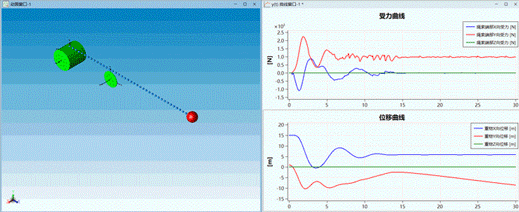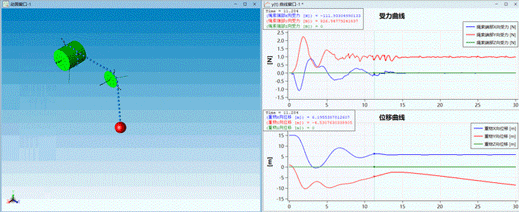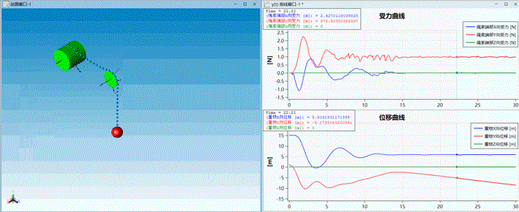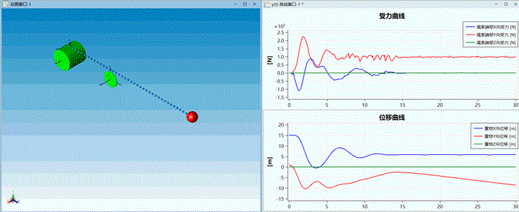
△ 动画效果
2.4 滑移副模型构建
滑移副在工程中应用广泛,小到渡江用的滑索,大到舰载机着陆时的尾钩,都可以建模为滑移副。那么绳索上使用的滑移副应该如何用方程描述呢?


△ 滑移副的应用
(上:过江用的滑索,下:舰载机的尾钩)
不考虑摩擦的滑移副可以由如下约束方程描述:
其中,表示绳索上一点,
表示与绳索连接的刚体或柔性体上的一点,
是维数为3的拉格朗日乘子。利用滑移副我们搭建了一个简单的滑索模型,模拟了在重力作用下刚性杆在绳索上的滑动现象,一起来看看效果吧!
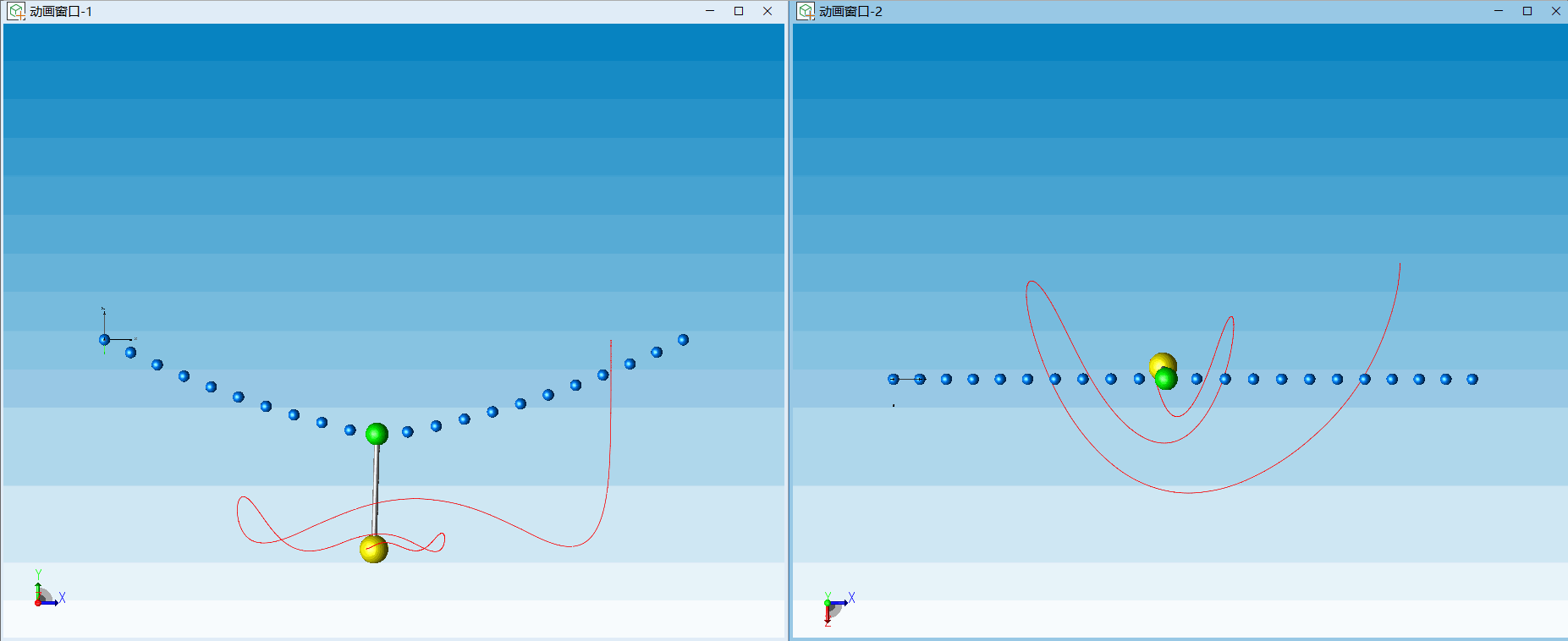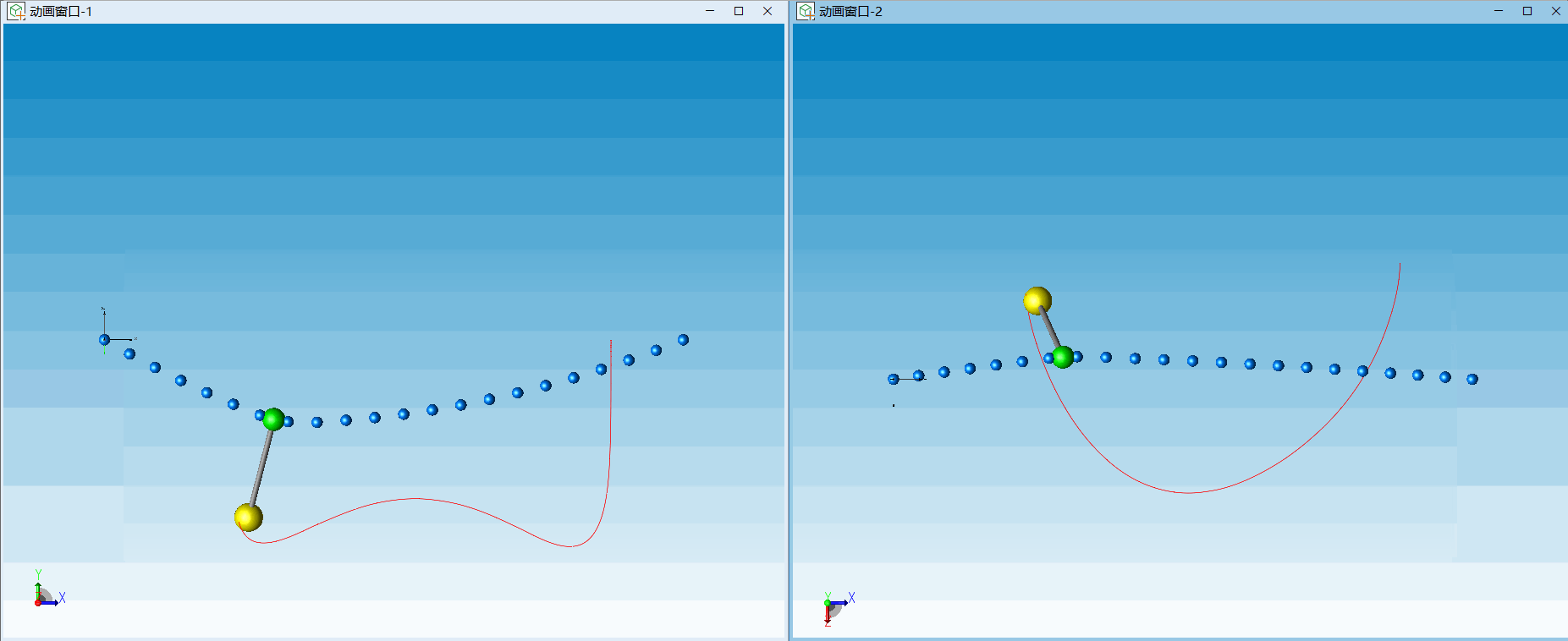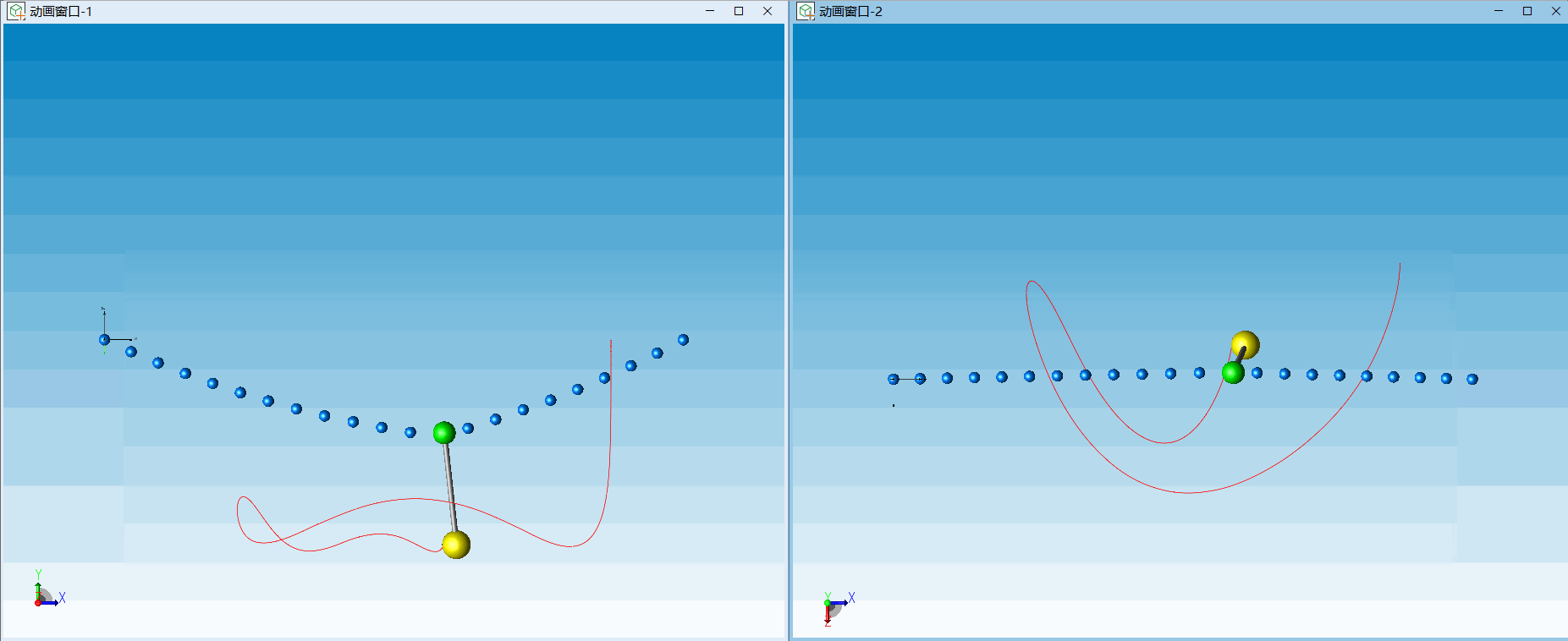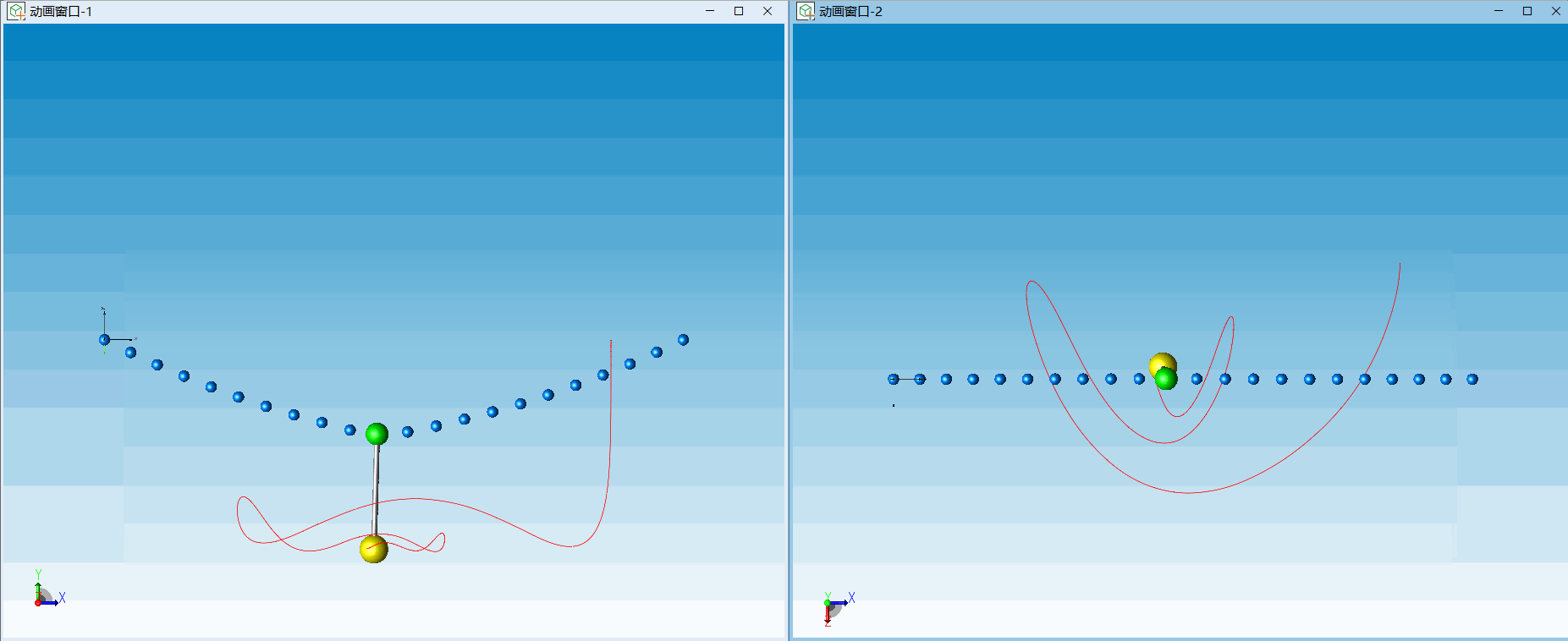
△ 滑索动画效果(左:正视图,右:俯视图)

绳索、滑轮、卷扬和滑移副组件涵盖了滑轮绳索传动系统中最为重要的部分。通过拖拽的方式将滑轮、卷扬、绳索有机的结合在一起,从无到有地搭建一个绳索传动系统是非常方便快捷的。千万别小看了一根绳子的威力,由它还可以衍生出传送带、绳网等模型,从日常生活到军工国防都能看到它的身影。让我们来欣赏一下绳子的魅力吧!
3.1 带传动典型应用
带传动模型由一个主动轮、一个被动轮和一个传送带模型组成,其中主动轮由转动接口外接转速信号驱动。
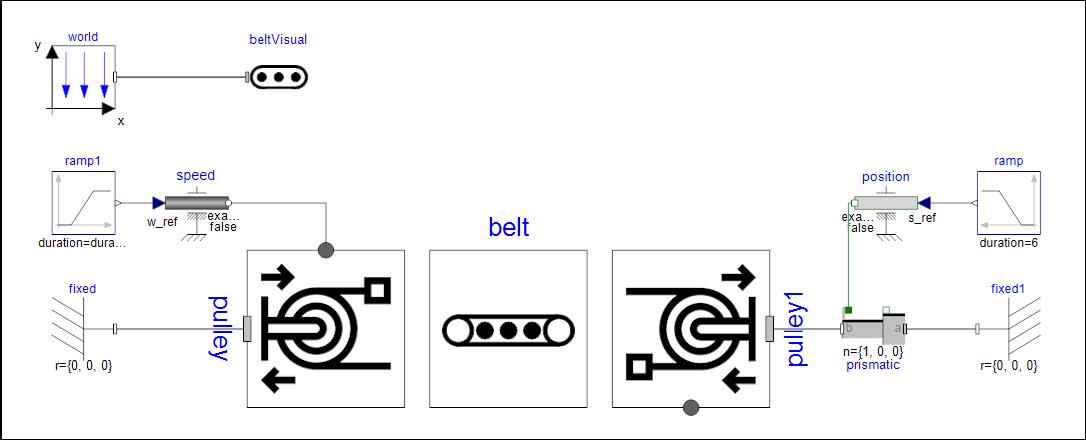
△ Modelica系统模型
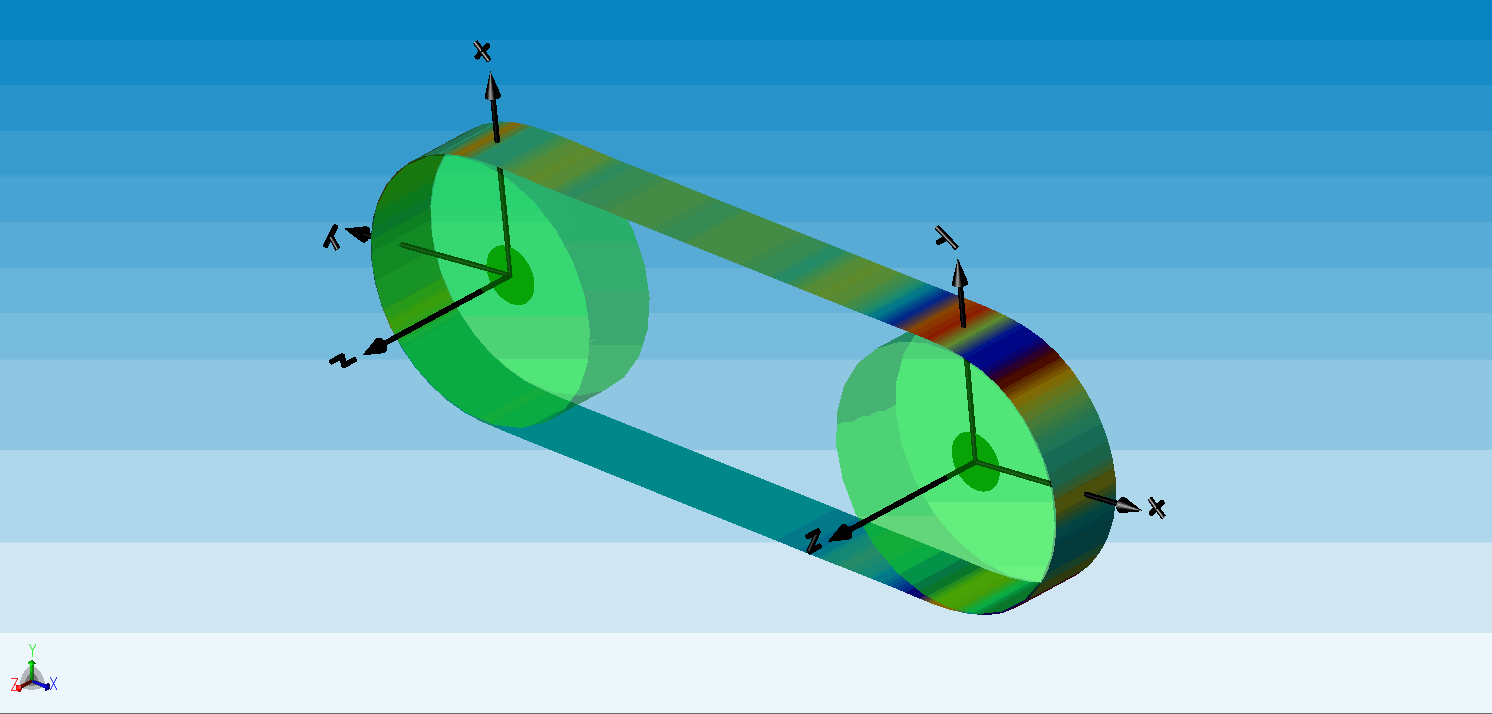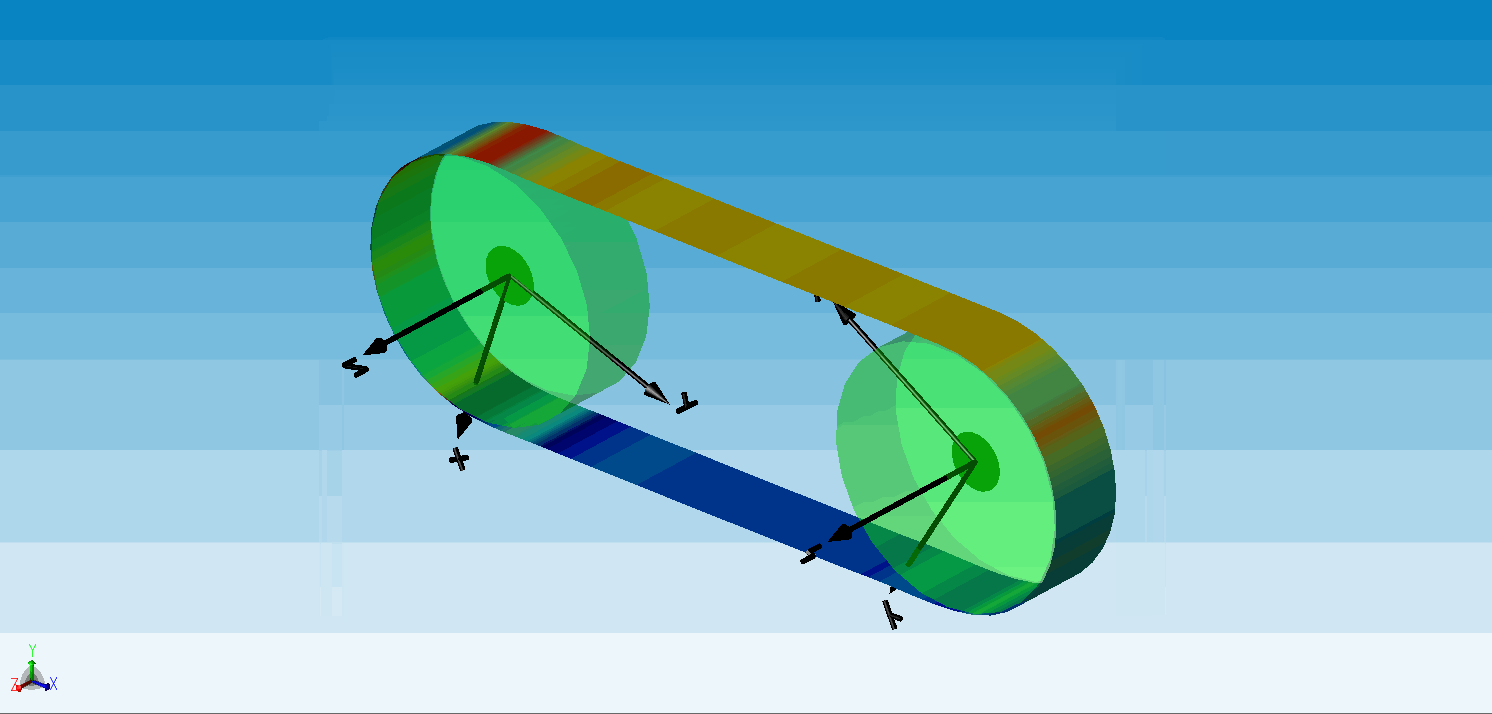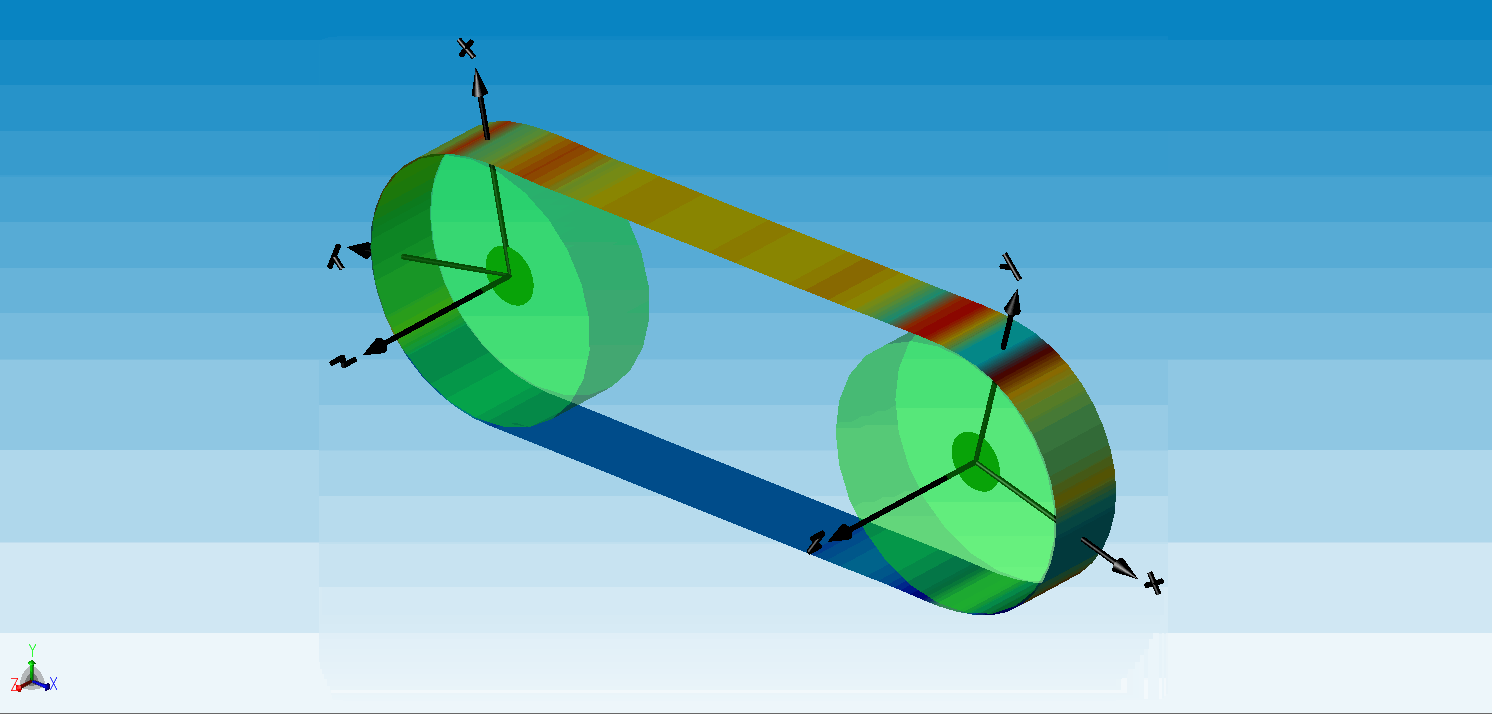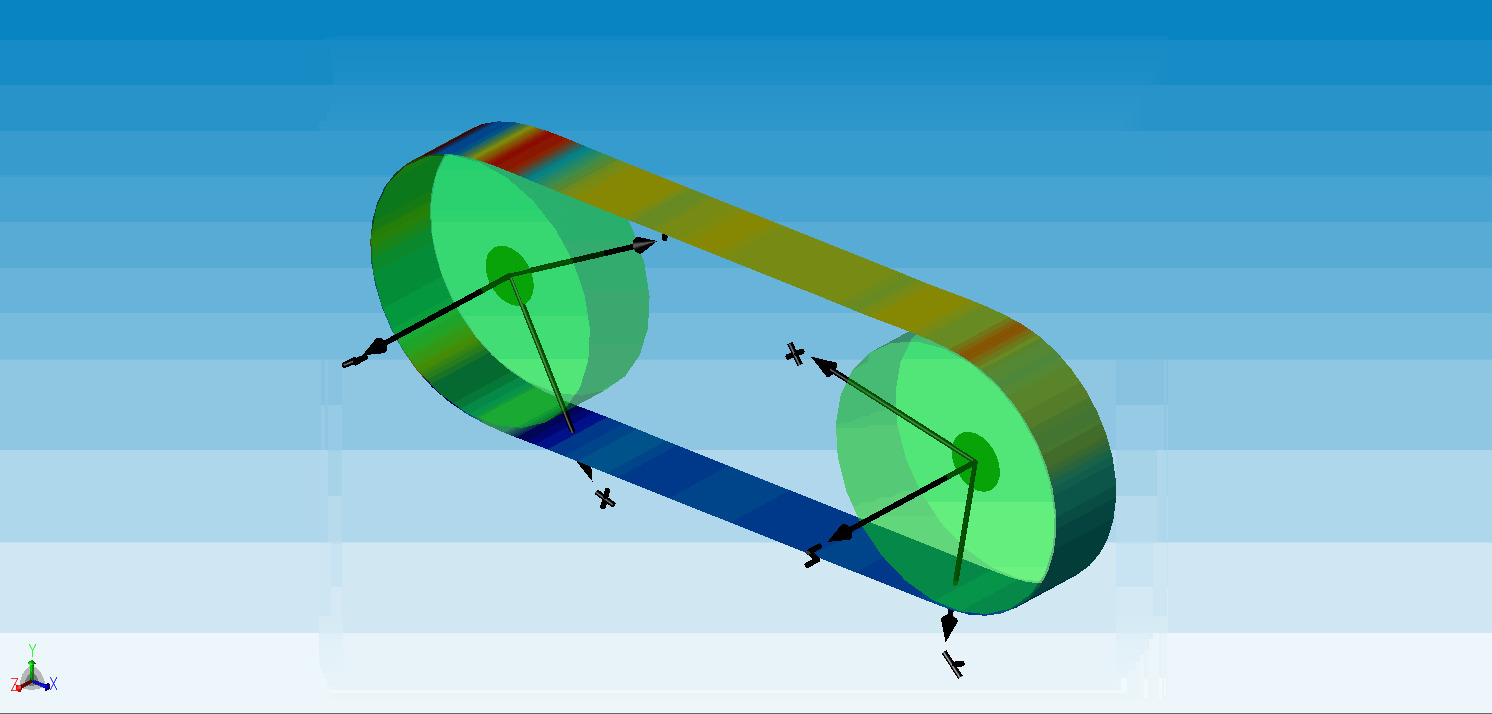
△ 传送带动画(云图显示的是传送带的轴向应力)
3.2 绳网典型应用
绳网模型对外开放了四个角点处的Frame接口,通过改变角点处的边界条件,可以轻松实现不同使用场景下的绳网建模。
场景1:四角固定的绳网。
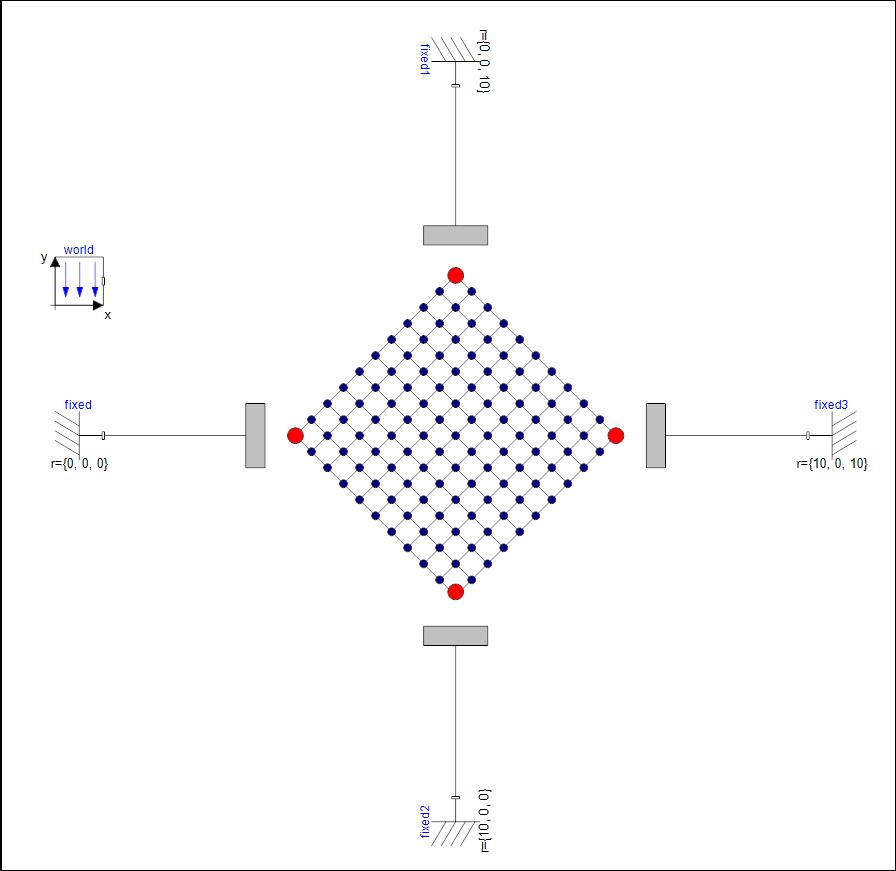
△ Modelica系统模型
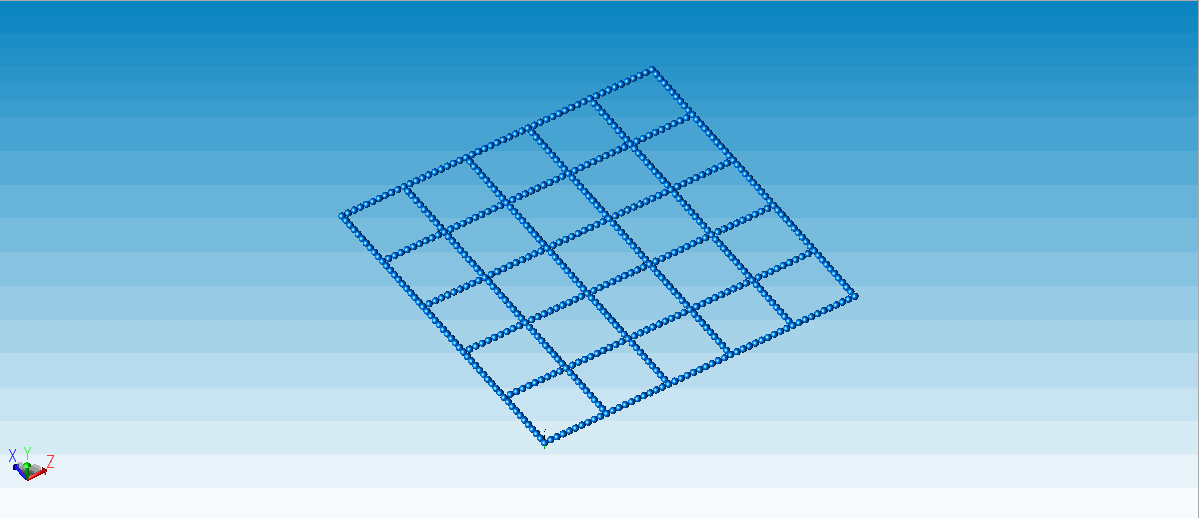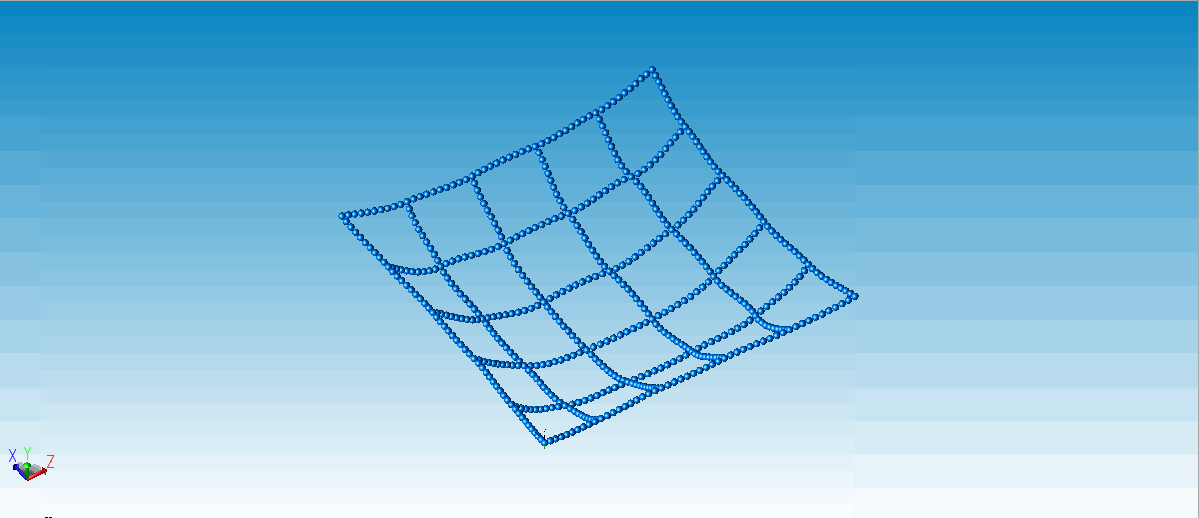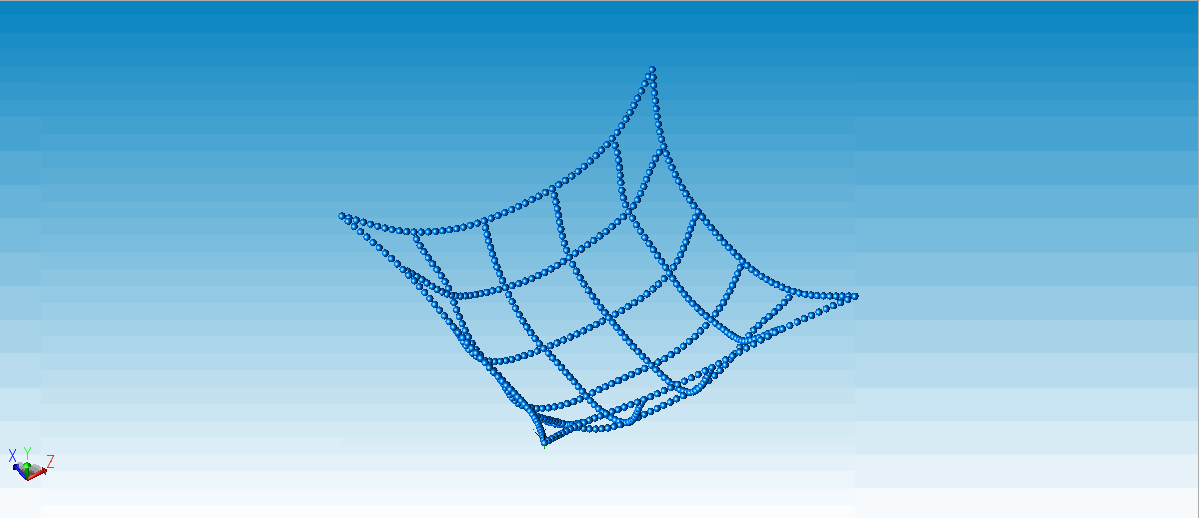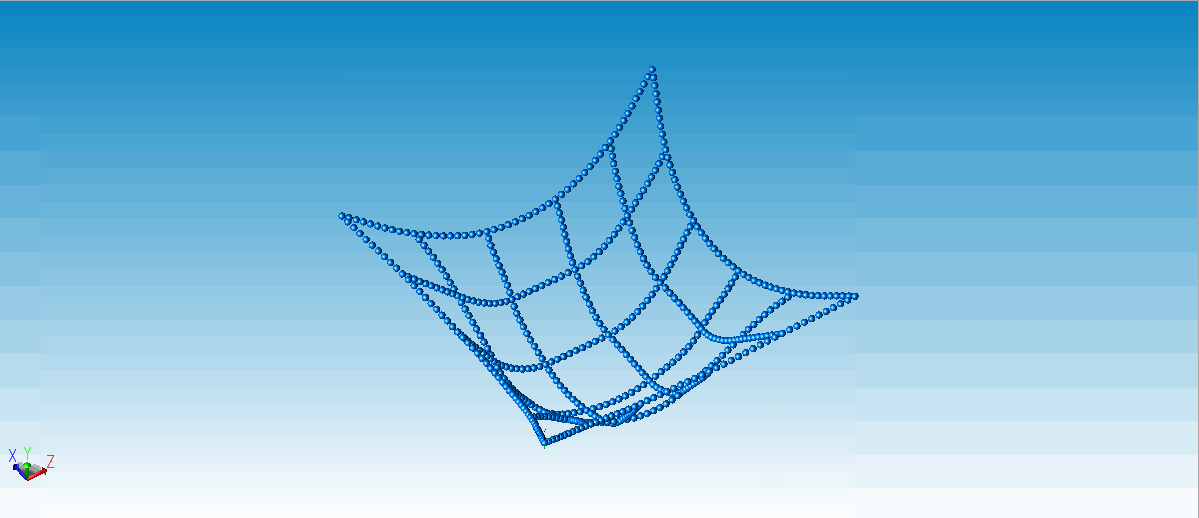
△ 绳网1(四角固定)
场景2:四角沿对角平动的绳网。
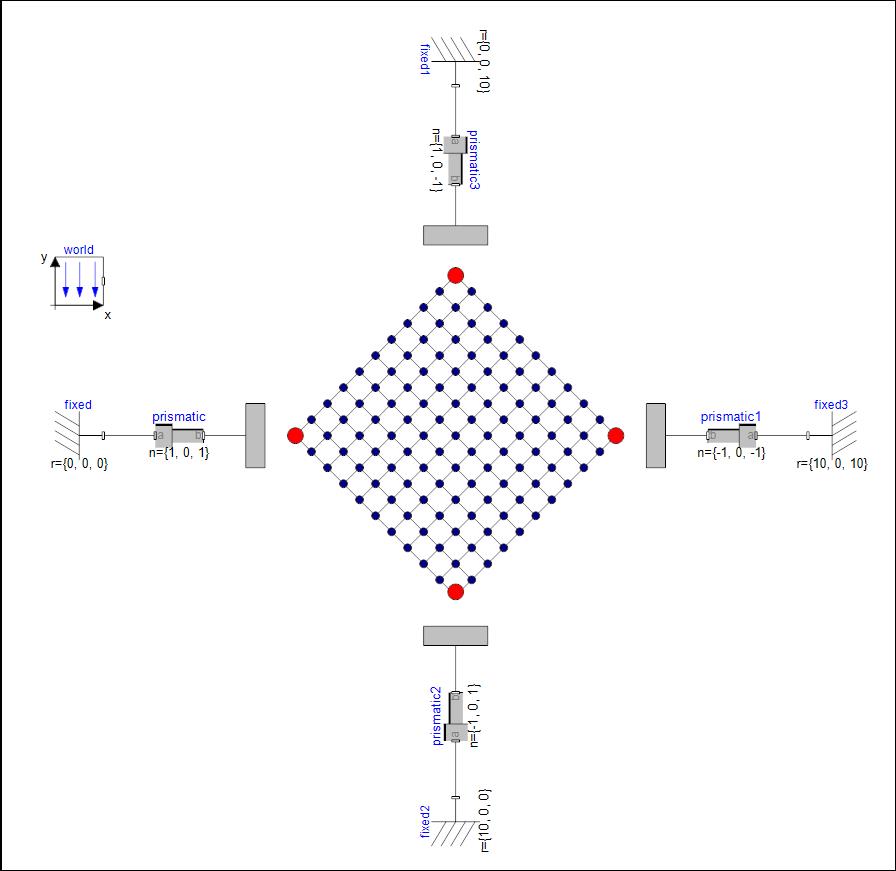
△ Modelica系统模型

△ 绳网2(四角沿对角平动,绳网在重力作用下收拢)
场景3:三角固定,一角悬挂重物的绳网。
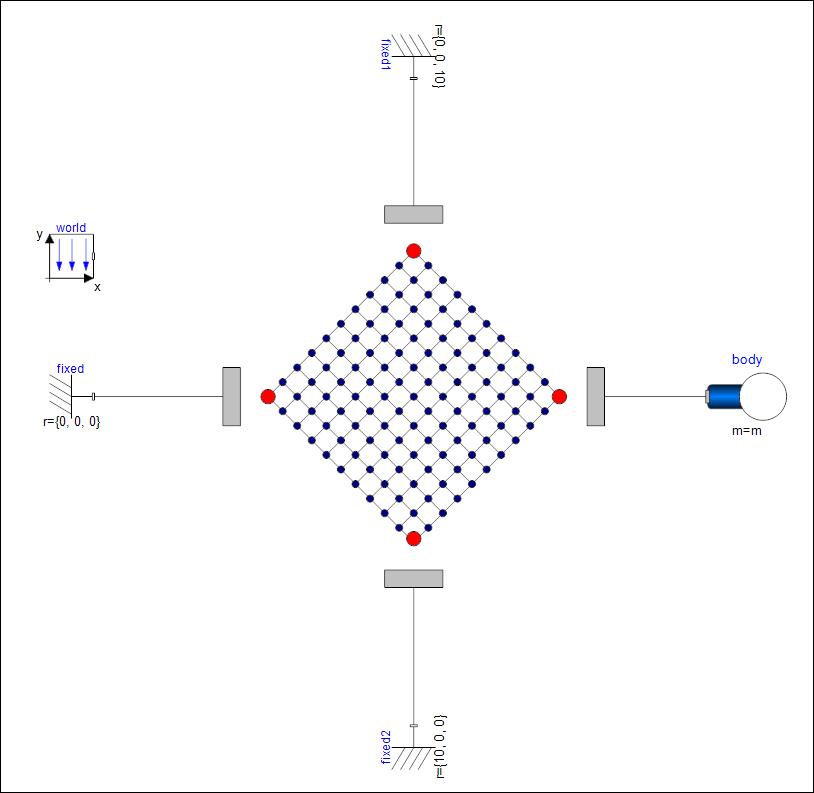
△ Modelica系统模型
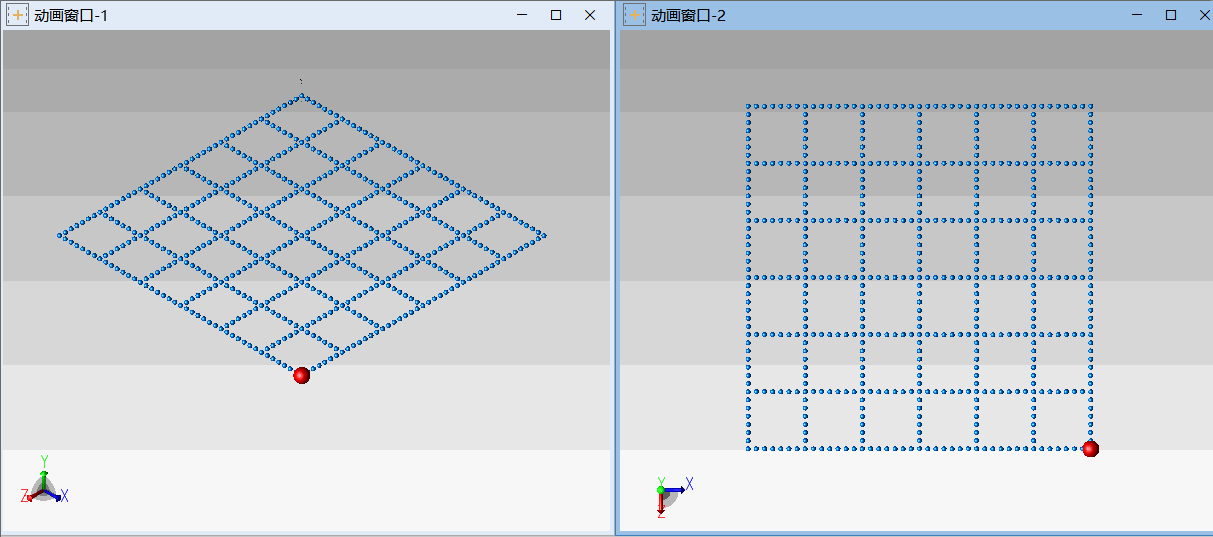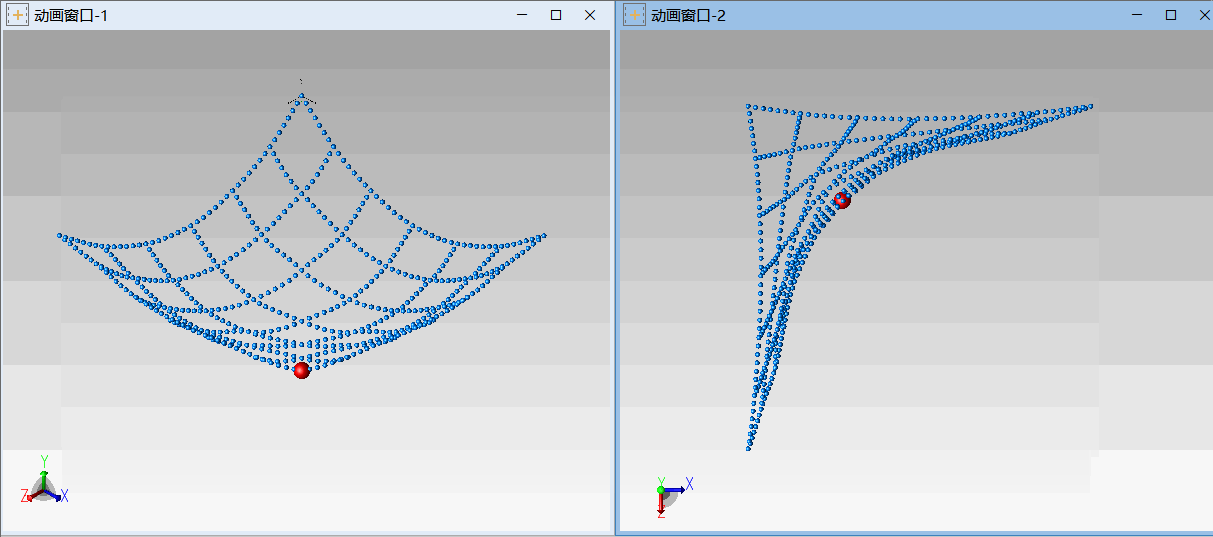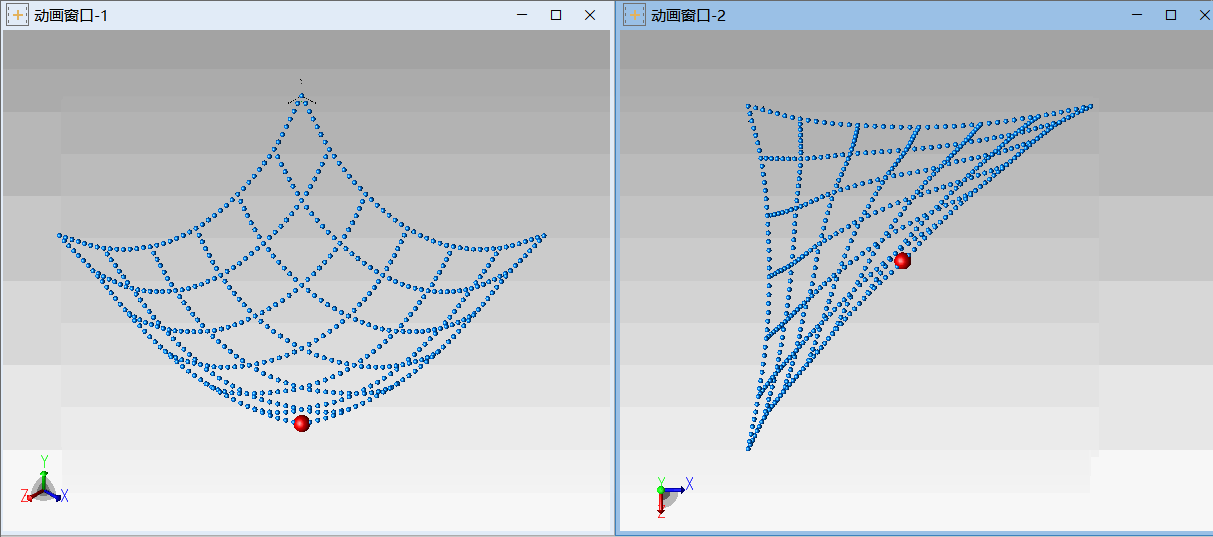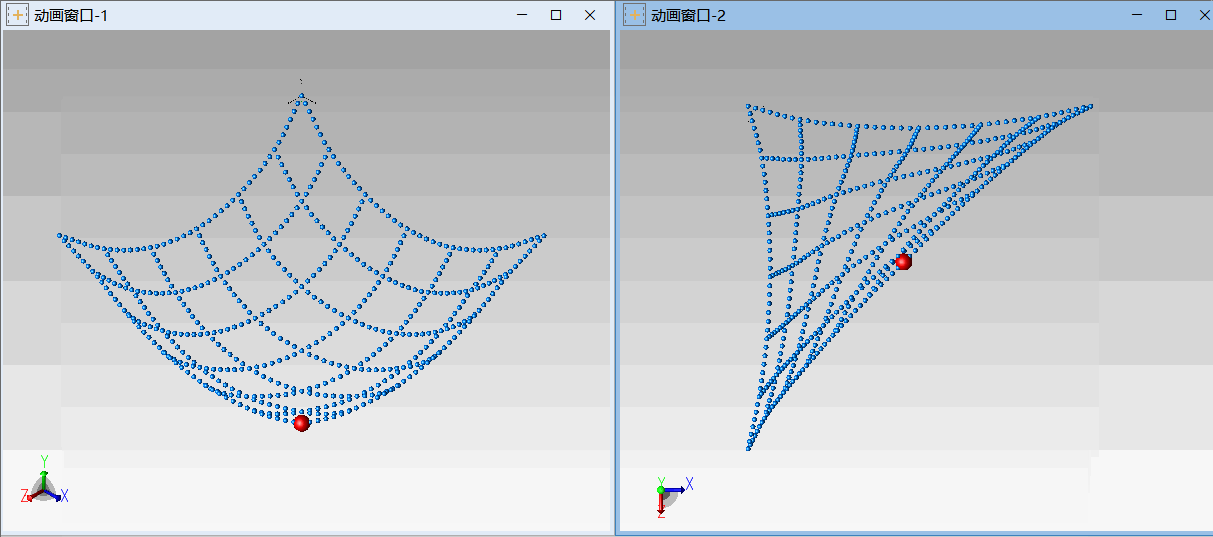
△ 绳网3(三角固定,一角悬挂重物)
3.3 龙门吊典型应用
龙门吊模型主要由两根绳索、两个卷扬、一个集装箱和龙门吊机架组成,模拟了重物在卷扬和机架的共同作用下的运动情况。
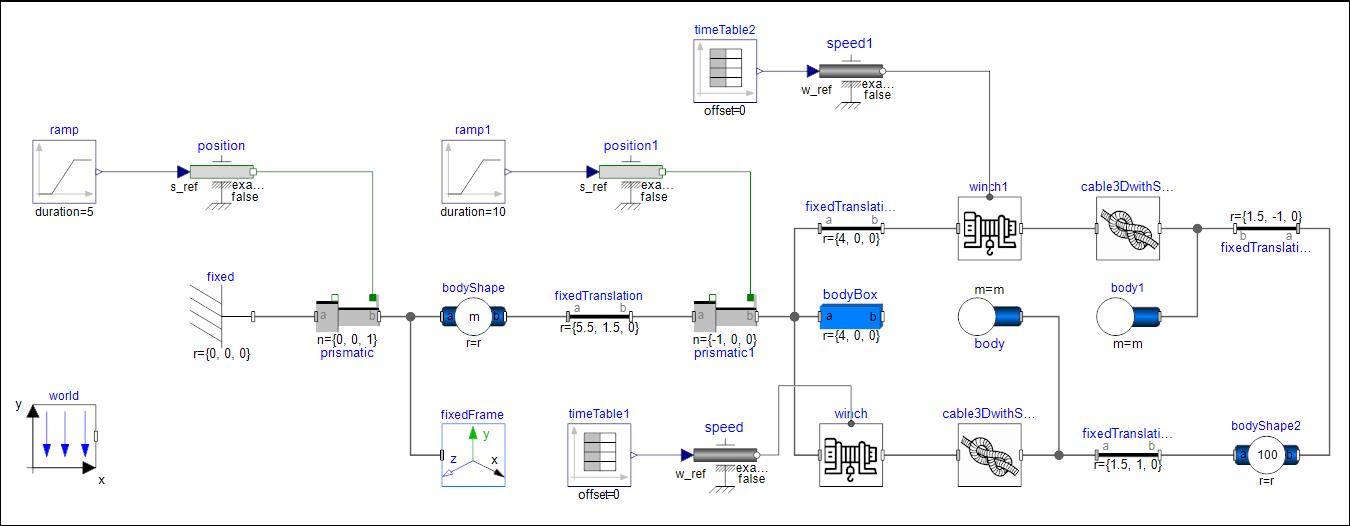
△ Modelica系统模型
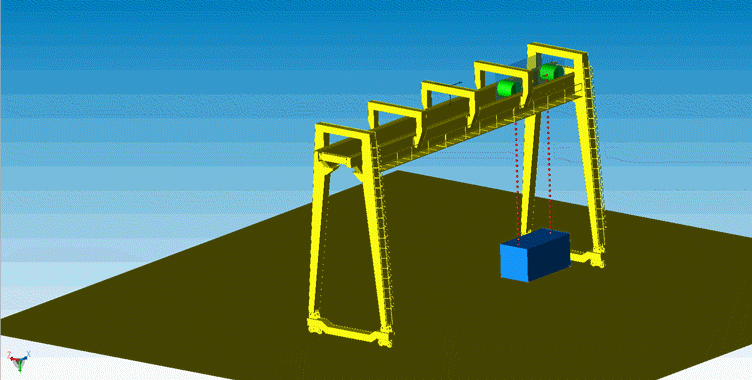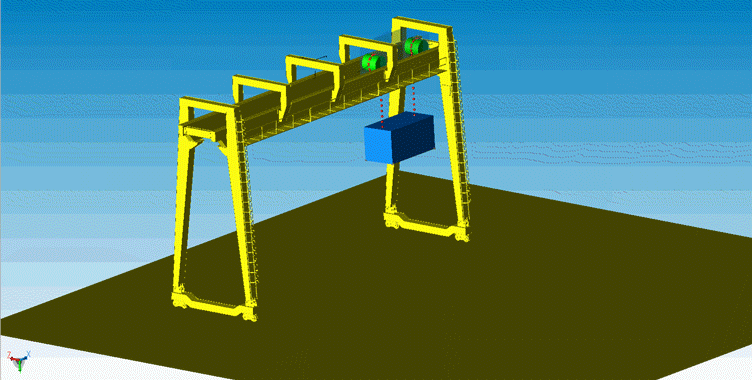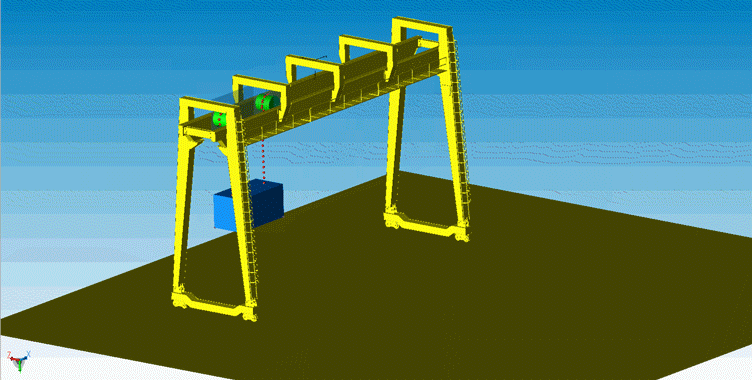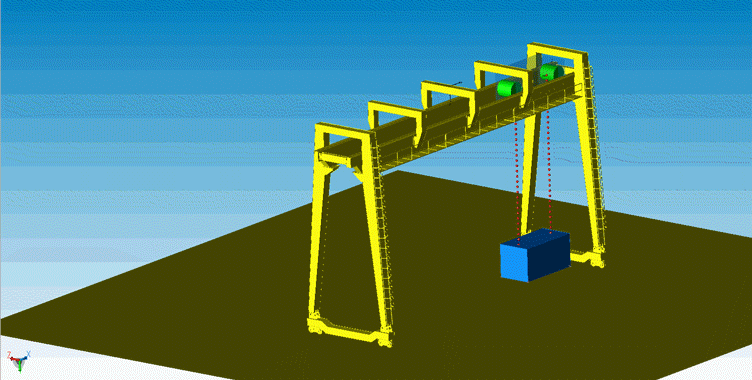
△ 重型机械中的龙门吊

绳索传动系统的仿真涵盖了刚体动力学、柔性体动力学、接触力学等方面的内容。本文基于有限单元法,实现了三维柔性绳索模型的搭建;利用Modelica多体库,实现了绳索和刚体的刚柔耦合分析;利用接触力学的摩檫力模型,实现了绳索与滑轮的接触行为仿真。本文尚未涉及的内容从建模层面来看有绳索的自接触、高效的接触检测算法、先进的绳索单元(如ALE-ANCF单元)等,从求解层面来看有大型稀疏矩阵的组装、求解等,这些都是值得深入研究的问题。MWORKSSysplorer为绳索传动系统的建模仿真提供了广泛且深入的平台支持,一个稳定、高效且用户友好的绳索传动模型库将在不久后推出,敬请期待~




