C++算法初级9——递归

递归，简单地来说，就是一个函数自己调用自己。

函数f()就好像是工厂中生产零件的模板，每次我们调用函数f()的时候，都会依照模板生产一个新的零件，名字叫“函数f()”。我们调用了很多次函数f()，也就是生产了很多名字相同的零件，它们的模样也相同，但是它们是不同的零件，因为我对一个零件操作不会影响到其他零件。

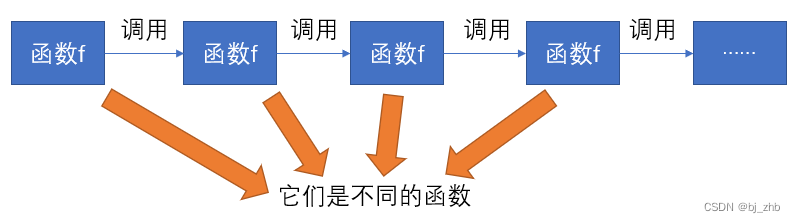
另外，两个函数相互调用也算是递归的一种，只要涉及到“函数自己调用自己”，都可以称为递归。

#include <bits/stdc++.h>
using namespace std;void g();void f() {g(); // f调用g
}void g() {f(); // g调用f
}int main() {f();return 0;
}

递归求阶乘

输入非负整数n，使用递归法求出n的阶乘，答案对998244353取模。

我们设f(n)为n的阶乘，那么根据阶乘的定义，我们可以得到：

f(0) = 1 // 初始值
f(n) = f(n-1) * n // 递归公式

//递归求阶乘
# include<bits/stdc++.h>
using namespace std;
const int MOD = 998244353;int fac(int n)
{if(n==1)return 1;elsereturn (long long)f(n-1) * n % MOD; 
}int main()
{int n;cin>>n;cout<<fac(n)<<endl;return 0;
}

容易发现，递归的执行过程是“从上到下，再回到上”：

我们最开始是想知道f(5)的答案，但是想要知道f(5)就必须知道f(4)
想要知道f(4)就必须知道f(3)
……如此刨根问底，最后到了f(0)
我们直接得到了答案，然后再一层一层地返回，逐渐融合成我们想要的答案

因此，我们也可以分析出，该算法的时间复杂度是O(n)：“从上到下”的过程是O(n)，“再回到上”的过程也是O(n)，加起来一共是O(n)。

递归求斐波那契数列

输入正整数n，使用递归法求出斐波那契数列的第n项，答案对998244353取模

//递归求斐波那契数列
# include<bits/stdc++.h>
using namespace std;
//输入正整数n，使用递归法求出斐波那契数列的第n项，答案对998244353取模
const int mod=998244353;
int fib(int n)
{if(n==1||n==2)return 1;elsereturn (fib(n-1)+fib(n-2))%mod;
}int main()
{int n;cin>>n;cout<<fib(n)<<endl;return 0;
}

从归纳的角度思考递归
对于任意的递归函数，我们都可以从数学归纳法的角度去理解它，再抽象一点，就是：

1. 这个函数设计出来的目的是什么？

求斐波那契数列。

2. 在边界条件上，这个函数正确吗？

正确。

3. 这个函数能正确利用递归处理出来的结果吗？

可以正确使用。

因此这个函数是正确的。

第一点尤为重要！在理解一个递归函数之前，我们必须知道这个函数的目的是要干什么，这样才能使用数学归纳法。

这也警示我们，在写递归函数的时候，

不要让一个函数干两件事情！

不要让一个函数干两件事情！

不要让一个函数干两件事情！

只有每个函数干唯一指定的事情，才能保证写出来的代码是可靠易读易修改的。

第二点是我们大家都能想到的点，但是经常会忘记一些特殊情况导致漏写边界条件。在结果出问题的时候，需要检查一下是不是有什么边界条件忘记了。

第三点是递归最难理解的地方，这里分享一个小窍门：

在一个函数递归调用自己的时候，我们可以直接假设这个函数是一个已经写完，并且功能完善的函数，它能保质保量地完成我们想让它做的事情（这其实就是数学归纳法的前提假设）。

千万不要把递归函数展开，千万不要尝试研究递归的过程是什么样的，因为人脑根本无法承受如此大的数据量，我们只能用数学归纳法来保证递归函数的正确性。

同时，这也是为什么我们要求在写函数之前想好这个函数的任务，并且在写函数的过程中，这个任务始终不能变化，因为这是我们使用数学归纳法的前提，我们需要假设这个函数能完美地完成这个任务，才可以肆无忌惮地放心递归调用它。

那么，函数的正确性我们已经理解了，复杂度如何分析呢？

由于递归函数总是在边界条件处结束，因此我们可以重点关注边界条件被执行的次数，粗略地估计算法的复杂度。

比如求斐波那契数列的算法:

边界条件if( n == 1 || n == 2 ) return 1;执行的次数，其实就等于这个斐波那契数本身（这个数是由这样的1累计起来的），比如计算f(10)的复杂度就至少是O(f(10))，计算f(n)的复杂度就至少是O(f(n))，我们可以粗略地将这个算法的复杂度估计为“指数级”（因为斐波那契数本身的增长速度就是指数级）。这就足够了。

上面讲了如何理解一个递归算法，那么我们如何自己用递归算法解决问题呢？

仍然是牢记这三板斧：

确认并牢记这个递归函数的功能，始终不能改。
仔细检查，写对边界条件。
递归调用自己时，放心大胆地用，假设这个函数就是对的。