金融风险计量:数据平滑方法及逆平滑分析

摘要及声明
1:本文从风险分析的角度简单介绍数据平滑方式,重点介绍低频数据的逆平滑分析;
2:本文主要数据通过爬虫获取;
3:模型实现基于python3.8;
处理金融数据时我们经常会遇到有噪音的数据,或是平滑后却丢失了很多原始信息的数据。针对这两种数据类型,笔者从风险计量的视角总结了数据平滑技巧及低频数据的逆平滑分析技术,本期主要内容如下:
目录
1. 数据平滑
1.1 去掉/替换极端值
1.2 移动平均
1.3 数据稀疏
2. 逆平滑技术
2.1 为什么需要逆平滑
2.2 逆平滑思路
2.3 从平滑推导逆平滑
3. 代码实现
3.1 数据准备
3.2 逆平滑还原
3.2.1 交易数据还原
3.2.2 低频经济数据还原
4. 总结
5. 往期精选
1. 数据平滑
先声明一下,数据平滑方法网上其实很多文章都介绍过,本来笔者是不打算写的,但如果跳过平滑技术直接介绍比较冷门的逆向平滑分析又很突兀。因此简单介绍下去掉/替换极端值,移动平均及数据稀疏这三种数据平滑方式及其优缺点,目的在于引出逆向平滑分析。不感兴趣的可以直接跳过,看逆平滑部分。
在进行数据分析或建模过程中,数据的噪音很大程度上会使模型有效性大打折扣。以某口罩概念公司的财报数据为例,在疫情爆发期间,该公司受口罩需求影响每股营收从疫情前的1块钱不到猛飙到12元, 如图一:

图一:某口罩概念公司的每股收益数据
统计结果如下,该公司2018-2022年三季度的季度平均每股收益为3.13元。
| 统计指标 | 参数 |
| count | 26.00 |
| mean | 3.13 |
| std | 3.86 |
| min | 0.26 |
| max | 12.50 |
表一:原始数据统计结果
但显然疫情期间的业绩增长是不可持续的,该公司业绩也在2021年后迅速回落。可是疫情期间出现的异常数据的确对数据分析造成了极大的阻碍,模型对这样的数据会感到很“困惑”。其实有很多种方法消除这样的异常噪音以提高模型有效性,例如简单去掉极端值,移动平均,数据稀疏,还有加各种滤波器,数据加权线性回归等等。
1.1 去掉/替换极端值
最为简单粗暴的方式,小学生都知道"去掉一个最高分,去掉一个最低分”的道理。去掉2020年1月-2021年12月的数据后统计结果如下:
| 统计指标 | 平滑前 | 平滑后 |
| count | 26.00 | 19.00 |
| mean | 3.13 | 1.30 |
| std | 3.86 | 0.75 |
| min | 0.26 | 0.26 |
| max | 12.50 | 2.64 |
表二:极端值替的换统计结果
去掉极端值后走势如图二:

图二: 某口罩概念公司的每股收益数据(橙线:去掉2020年极端值)
每股收益均值平滑前为3.13元,平滑后为1.30元,相差近1.41倍,而这差的1.41倍全是2020年仅1年时间贡献的。除了直接删除,使用历史数据的均值,最小值或最大值替换极端值也是可以的,这里就不展示了。
直接去掉/替换极端值在完全消除了异常数据影响的同时也使得原始数据完全丧失了2020年的信息,其它年份的信息则是被完全保留了下来,笔者认为这是一种非对称的数据平滑方式。
1.2 移动平均
说白了就是均线,规定不同的移动窗口及步长即可得到相应的平滑数据。比起直接删除极端值,它的好处在于降低了信息的损失。例如,以一年为一个移动窗口,步长为1进行简单移动平均可得图三,还是可以很明显看出疫情对于数据造成的影响,换句话说移动平均比起直接删除数据来说更大程度上保留了数据所携带的信息:
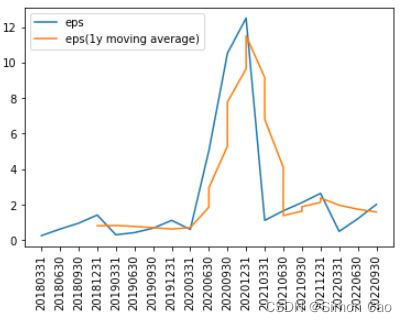
图三:每股收益移动均线(1年)
统计如下:
| 统计指标 | 平滑前 | 平滑后 |
| count | 26.00 | 23.00 |
| mean | 3.13 | 3.41 |
| std | 3.86 | 3.29 |
| min | 0.26 | 0.64 |
| max | 12.50 | 11.52 |
表三:移动平均统计结果(1年)
诡异的是,平滑前均值3.13元,平滑后为3.41元。移动平均不仅没有使均值变小,反而使得均值变大了。
这是因为移动平均的步长仅仅为1,于是原始数据中的极端值会持续对移动平均数据造成影响,因此拉高了整体均值。如果移动窗口越大,那么极端值造成的持续性影响也会更高,如图四:

图四:每股收益移动均线(2年)
统计结果可以看到,当不断提高移动窗口大小时,均值会越来越大(但是这个变大的过程是有一定限度的,随着移动窗口不断变大,不断接近原始数据集大小时,均值其实会向着原始数据的均值靠拢):
| 统计指标 | 平滑前 | 平滑后(1年) | 平滑后(2年) |
| count | 26.00 | 23.00 | 19.00 |
| mean | 3.13 | 3.41 | 3.84 |
| std | 3.86 | 3.29 | 2.41 |
| min | 0.26 | 0.64 | 0.73 |
| max | 12.50 | 11.52 | 7.30 |
表四:移动平均统计结果对比(1年,2年)
从上面的实验来看,均值(一阶矩)上似乎完全没有平滑的效果。但从标准差(二阶矩)的维度上看,移动平均的确降低了数据的波动率,而且随着移动窗口不断变大,数据的波动率也不断变小。总的来说移动平均是可以降低原始数据的波动率的,因此达到了平滑的目的。但是,笔者想补充一点:移动平均是具有滞后性的,而且时间越长,滞后效果越明显(这和K线均线的原理一样)
最后,除了简单移动平均,还有加权移动平均,无非是给的权重不一样而已,这里就不展示了。
1.3 数据稀疏
其实就是对原始数据进行抽样,这样就可以达到稀疏的目的。可以是随机抽,也可以是等间距抽。下面以5个财报期进行等间距抽样:

图五:数据稀疏(5个财报期等间距抽样)
统计结果如表五:
| 统计指标 | 平滑前 | 平滑后 |
| count | 26.00 | 6.00 |
| mean | 3.13 | 1.83 |
| std | 3.86 | 1.75 |
| min | 0.26 | 0.26 |
| max | 12.50 | 5.04 |
表五:数据稀疏(5个财报期等间距抽样)
可以看到,进行数据稀疏也可以达到平滑数据的目的,但缺点也是很明显的,例如对于周期性数据,数据稀疏很难体现出周期性特征,其次数据稀疏只保留了原始数据中的某些关键点,其它数据点上的信息则完全丧失,也是种非对称的平滑方式。
2. 逆平滑技术
关于数据的逆平滑网上能查到的资料少之又少,因此也是笔者打算重点讲解的部分。
2.1 为什么需要逆平滑
前面说了几种多数据平滑方式,其目的无非在于降低数据噪音,提高模型有效性,用统计学的专业术语来说就是为了满足最大似然估计的要求。但是,极端数据或者数据的波动未必都是噪音,过度的平滑反而会让原始数据携带的信息丢失很多。于是,这里引入数据的逆平滑技术用于将过度低估波动率的数据还原,这对于风险分析意义重大。
举个例子,笔者构建一个指标叫每股收益风险回报率(自创的),其分母为EPS的波动率,分子为EPS:
这个指标和夏普比率类似的:如果将标准差看作是风险,每股收益风险回报率即是每单位EPS的风险对应多少的EPS回报。以表四中数据为例进行计算:
| 指标 | 平滑前 | 平滑后(1年) | 平滑后(2年) |
| mean | 3.13 | 3.41 | 3.84 |
| std | 3.86 | 3.29 | 2.41 |
| EPS risk return ratio | 0.81 | 1.04 | 1.60 |
表六:每股收益风险回报率对比
随着平滑力度加大,使得标准差不断变小,每股收益的风险回报率也在不断提高。但这是种欺骗——事实是,承担1单位风险对应的仅仅只有0.81的收益。
2.2 逆平滑思路
如图六,之前平滑数据其实一直都在走图六左边的路径,所谓逆平滑其实就是一个反向还原的过程(图六右边的路径):

图六:平滑与逆平滑
但现实中的情况远不是把箭头反过来这么简单,下面笔者分三种情况讨论。
1): 知道原始数据
例如股票数据就是这样的,我们知道均线数据,但其实也很容易获取到高频的K线原始数据。之前笔者在数据平滑部分所做的处理也是一样,笔者其实是直接拿到了全部数据然后进行平滑操作,也就是说其实笔者知道原始数据是什么。这种情况下所谓的逆平滑就成了一直笑话,既然都知道原始数据,直接利用原始数据计算即可,何必这么复杂?
2): 只知道原始数据参数
如果不知道原始数据,但知道平滑数据,还有原始数据的方差其实就可以通过逆向计算对原始数据进行简单还原,方法其实也很简单,根据分布随机生成数据。但如果想要进行更精确的还原,还需要知道原始数据的三阶矩甚至四阶矩等更多信息,例如偏度,峰度等。知道原始数据的统计参数越多,还原就越精确。
但是!这种情况基本不太可能出现,这是一个悖论:知道原始数据那么多详细的统计信息但却不知道原始数据?难是上帝在为难你?除非是进行一些主观的预测,只能主观估计一些原始数据参数,那么通过逆向生成数据可以对平滑数据进行还原。
3): 只知道平滑后的数据
一般来说最常碰到的都是低频的数据(数据稀疏后的),且无法得知原始数据是什么样。很多低频的数据就是平滑数据,例如其实每天都会产生新的GDP数据,但统计局无法将GDP数据做到日线级别,因此每个季度公布一次的GDP数据就是一种数据稀疏后的平滑数据,并且我们不知道它每天的原始数据是什么样的。再比如市场上的房地产,对冲基金等很多评估类数据,由于无法做到高频,它们也都是平滑后的数据。
处理这种数据的思路就是曲线救国了,如图七:

图七:无法得知原始数据时的逆平滑思路
由于无法得知原始数据集的任何信息,之前想通过平滑数据直接逆向生成原始数据的方式(虚线)就行不通了。好在有平滑数据,这为估计原始数据集的统计参数提供了一个突破口。通过平滑数据的统计参数,借助逆平滑即可估计出原始数据集的参数。
1)和2)是比较无脑的情况,接下来笔者就重点对3)这种情况下的逆平滑进行推导。
2.3 从平滑推导逆平滑
假设原始数据集,设
为
平滑后的数据,那么通过函数[1]即可描述平滑程度:
其中,即为平滑程度;因为平滑作用,一般来说
取值范围是[0,1],
越接近0,那么平滑后的
越接近原始数据集
;
越接近1,那么平滑后的
越接近平滑后的数据
。
除了平滑程度,还可以解读为平滑后数据
与
的自回归系数。
因为目的在于对原始数据集的参数进行估计,以方差为例,该问题就变成了已知[1]式及平滑后数据集的统计参数,如何求解原始数据集的方差?
将方差写做,[1]式稍微变下形即可求
;将
独立出来然后两边取方差,如[2]式:
下面对[2]进行变形得到[3]式:
[3]式方差部分展开:
由于都是同一个数组中的数值,其实近似相等的,因此:
如果将看作自回归系数,那么:
综上,[4]式可以化简最后得到[5]式:
[5]式的神奇之处在于,只知道平滑后的数据,理论上可以反向推导出原始数据集
的方差,也就是图七中利用平滑数据参数反向推导原始数据参数的过程。
不过,[5]式其实严格来说不能算作是一个等式。因为之前推到的时候用过几个近似条件,这里把等号改成约等号会更严谨。
3. 代码实现
由于直接采用未知的原始数据集无法比较数据逆平滑后的还原效果,笔者先采用上证指数日涨跌幅数据作为原始数据,在该数据集中进行等间距抽样得到平滑的数据集,最后笔者试图利用逆平滑技术对平滑后数据集的方差进行还原。
3.1 数据准备
数据方面笔者爬取了东方财富网上证指数从2018年至今的数据,程序的源代码笔者上传到资源里了,需要的可以点我的主页,在资源里下载,也可以点击这个链接直接传送:上证指数日线数据获取程序-CSDN文库。
什么?你问我爬虫是怎么弄的?这个网页是怎么解析的?为什么不po在博客里?数据获取那个专栏已经很久没更新了,其实之前笔者还写了几篇博客讲解爬虫技术的,但都因为数据版权问题没过审,实在是累了TAT,这里就不做过多详细的解释了。

运行资源中的代码后可以获取上证指数所有历史数据,下面笔者仅选取2021年至2023年的数据,共550个交易日数据:
print(data_set)trade_date open close high low vol amount pct_chg
20210105 3492.19 3528.68 3528.68 3484.72 407995935.0 5.680195e+11 0.734236
20210106 3530.91 3550.88 3556.80 3513.13 370230927.0 5.217995e+11 0.629130
20210107 3552.91 3576.20 3576.20 3526.62 405348227.0 5.457096e+11 0.713063
20210108 3577.69 3570.11 3588.06 3544.89 345557896.0 5.021708e+11 -0.170292
20210111 3571.32 3531.50 3597.70 3516.99 362479155.0 5.268959e+11 -1.081479... ... ... ... ... ... ... ...
20230406 3302.75 3312.63 3314.53 3296.06 327155424.0 5.065002e+11 0.002113
20230407 3312.48 3327.65 3328.85 3308.06 283032247.0 4.363728e+11 0.453416
20230410 3331.51 3315.36 3332.72 3309.92 340819845.0 5.164343e+11 -0.369330
20230411 3317.08 3313.57 3317.45 3298.25 320566055.0 4.668958e+11 -0.053991
20230412 3316.86 3327.18 3330.71 3315.40 343025315.0 4.820662e+11 0.410735
550 rows × 7 columns3.2 逆平滑还原
3.2.1 交易数据还原
1):实验1,对数据集进行2日的等间距抽取
data_set["pct_chg"] = data_set["pct_chg"]*100 # 转化成百分比print("原始数据标准差:", '%.2f'%(data_set["pct_chg"].std(), "%")
data_set_sampling = data_set[::2].copy() # 等间距抽取,拷贝到新的变量中
sample_std = data_set_sampling["pct_chg"].std()
print("平滑后数据标准差:", '%.2f'%(sample_std), "%")# 原始数据标准差: 0.98 %
# 平滑后数据标准差: 1.01 %可以看到,原始数据经过抽样平滑后标准差不仅没有变小,反而变大了,造成这一现象的原因是抽样过程中样本量减小,但却抽到很多高波动的数据。这算是很特殊的情况了,即数据平滑不仅没有产生平滑效果,反而使得数据更加不平滑。
下面尝试进行逆平滑看能否还原出原始数据的标准差。首先创建滞后变量,然后进行自回归分析:
data_set_sampling["pct_chg_lag"] = data_set_sampling["pct_chg"].shift(1)
data_set_sampling = data_set_sampling[1:]import statsmodels.formula.api as smf
model = smf.gls(data = data_set_sampling, formula="pct_chg~pct_chg_lag")
result = model.fit()
result.summary()# 回归分析
GLS Regression Results
Dep. Variable: pct_chg R-squared: 0.002
Model: GLS Adj. R-squared: -0.001
Method: Least Squares F-statistic: 0.5974coef std err t P>|t| [0.025 0.975]
Intercept 0.0738 0.061 1.206 0.229 -0.047 0.194
pct_chg_lag -0.0468 0.061 -0.773 0.440 -0.166 0.072
自回归系数为-0.05,也就是说是小于0的。
lam = result.params["pct_chg_lag"]
estimate_var = sample_std2 * (1+lam)/(1-lam)
print("原始数据集的标准差:", '%.2f'%(data_set["pct_chg"].std()), "%")
print("逆平滑估计的标准差:", "%.2f"%(estimate_var0.5), "%")
print("平滑数据集的标准差:", "%.2f"%(sample_std), "%")# 原始数据集的标准差: 0.98 %
# 逆平滑估计的标准差: 0.96 %
# 平滑数据集的标准差: 1.01 % 可以看到,平滑数据标准差为1.01%,由于是小于0的,逆平滑后标准差为0.96%,已经接近了原始数据集的0.98%。因此,在本次实验中,逆平滑的确成功将平滑数据较大的标准差进行了还原。
1):实验2,对数据集进行30日的等间距抽取
结果如下:
data_set_sampling = data_set[::30].copy()
sample_std = data_set_sampling["pct_chg"].std()
data_set_sampling["pct_chg_lag"] = data_set_sampling["pct_chg"].shift(1)
data_set_sampling = data_set_sampling[1:]model = smf.gls(data = data_set_sampling, formula="pct_chg~pct_chg_lag")
result = model.fit()
result.summary()# 回归分析
GLS Regression Results
Dep. Variable: pct_chg R-squared: 0.023
Model: GLS Adj. R-squared: -0.038
Method: Least Squares F-statistic: 0.3850 coef std err t P>|t| [0.025 0.975]
Intercept 0.2809 0.234 1.199 0.248 -0.216 0.778
pct_chg_lag 0.1541 0.248 0.620 0.544 -0.372 0.681lam = result.params["pct_chg_lag"]
estimate_var = sample_std2 * (1+lam)/(1-lam)
print("原始数据集的标准差:", '%.2f'%(data_set["pct_chg"].std()), "%")
print("逆平滑估计的标准差:", "%.2f"%(estimate_var0.5), "%")
print("平滑数据集的标准差:", "%.2f"%(sample_std), "%")# 原始数据集的标准差: 0.98 %
# 逆平滑估计的标准差: 1.01 %
# 平滑数据集的标准差: 0.87 % 本次实验中,平滑数据集的标准差为0.87%,是小于原始数据集的,也就是说抽样具有平滑效果。平滑数据标准差为1.01%,由于是大于0的,逆平滑后标准差为1.01%,已经接近了原始数据集的0.98%。因此,在本次实验中,逆平滑的确将平滑数据较大的标准差进行了还原。
眼尖的应该看出来了,以上两个自回归模型有效性都是比较差的,笔者认为这是逆平滑估计产生偏差的主要原因之一。感兴趣的可以用不同数据做更多实验,这里就不进行更多展示了。总之笔者测试下来发现,只要自回归模型不是特别特别离谱,大多数情况下逆平滑都可以取得不错的效果。当然,逆平滑毕竟是对原始数据集的估计,偏差是难免的。
3.2.2 低频经济数据还原
下面以我国GDP数据为例,和之前一样爬取2010年至今的GDP季度数据如下(单位亿元):
print(data_set)quarter gdp
2013Q1 129449.6
2013Q2 272968.2
2013Q3 425190.9
2013Q4 592963.2
2014Q1 140270.2... ...
2021Q4 1143670.0
2022Q1 270178.0
2022Q2 562642.0
2022Q3 870269.0
2022Q4 1210207.0 
图八:我国近十年GDP数据(单位亿元)
与之前一样,进行自回归分析:
GLS Regression Results
Dep. Variable: sample_gdp R-squared: 0.008
Model: GLS Adj. R-squared: -0.019
Method: Least Squares F-statistic: 0.2871 coef std err t P>|t| [0.025 0.975]
Intercept 4.871e+05 9.92e+04 4.912 0.000 2.86e+05 6.88e+05
gdp_lag 0.0926 0.173 0.536 0.595 -0.258 0.443
反向最优化:
lam = result.params["gdp_lag"]
estimate_var = data_set["gdp"].std()2 * (1+lam)/(1-lam)print("原始数据集的标准差:", '%.2f'%(data_set["gdp"].std()))
print("逆平滑估计的标准差:", "%.2f"%(estimate_var0.5))# 原始数据集的标准差: 291823.03
# 逆平滑估计的标准差: 320227.43求得GDP实际标准差为320227.43亿元,由于GDP没有高频数据,无法对逆向估计的效果进行直接评估。
4. 总结
本期主要介绍了数据的平滑及逆平滑分析。数据平滑有着诸多优点,但过度平滑的数据会导致数据所携带的信息大量丢失。在市场上存在着大量的低频数据,例如经济数据,另类商品的估值数据,房地产评估数据等等。往往这些数据都是平滑的,直接使用这些数据进行分析会低估其中风险。因此,逆平滑分析的必要性凸显出来,它对于分析低频数据的隐含风险有重要意义。但需要注意的是,本文所介绍的逆平滑并非对数据进行百分百的还原,而是借助平滑数据的统计参数估计原始数据的统计参数,这一过程中往往是存在误差的,具体还需要根据数据判断这种方法是否适用。
5. 往期精选
| 往期精选 | ||
| 系列 | 文章传送门 | 实现方式 |
| 基本面分析 | 实现GGM的理想国 | Python |
| PB指标与剩余收益估值 | Python | |
| Fama-French及PSM | Python | |
| GK模型看投资的本质 | Python | |
| 增速g的测算 | Python | |
| PE指标平滑 | Python | |
| PE Band | Python | |
| 技术分析 | 分类树算法 | R |
| 蒙特卡洛模拟 | Python | |
| 全连接神经网络模型 | Python | |
| 组合管理 | 券商金股哪家强——信息比率 | Python |
| 从指数构建原理看待A股的三千点魔咒 | Python | |
| 决策树学习基金持仓并识别公司风格类型 | R | |
| 杂谈类 | 垃圾公司对回报率计算的影响几何 | Python |
| 市场风险分析 | Python | |
| 金融危机模拟 | Python | |
您若不弃,我们风雨共济:)


