算法刷题日志

今天是星期几就加上多少天在最后

public class Main {public static void main(String[] args) {System.out.println(Math.pow(20, 22) % 7 + 6);}
}

这题是判断左右回文，且要保持单调性，因为回文数左右对称所以只需要判断左边是否单调递增。

public class Main {public static void main(String[] args) {long start = System.currentTimeMillis();int count = 0;for (int i = 2022; i <= 2022222022; i++) {if (isPalindrome(i) && check(i)) {count++;}}long end = System.currentTimeMillis();System.out.println(count);}
​private static boolean check(int num) {String s = num + "";for (int i = 0; i < s.length() / 2; i++) {if (s.charAt(i) > s.charAt(i + 1)) return false;}return true;}
​private static boolean isPalindrome(int num) {String s = num + "";int n = s.length() - 1;for (int l = 0, r = n; l < r; l++, r --)if (s.charAt(l) != s.charAt(r)) return false;return true;}
}

先用数组统计每个字母出现次数，再用list来存放答案，循环遍历查找出现次数最多的并存入list之中，大于max就更新list，等于的话同样也可以存入list

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;public class Main {static int[] a=new int[26];public static void main(String[] args) {Scanner sc=new Scanner(System.in);String s=sc.next();for (int i = 0; i < s.length(); i++) {a[s.charAt(i)-'A']++;}int max=0;List<Integer> list=new ArrayList<>();for (int i = 0; i < 26; i++) {if (a[i]>max){list.clear();max=a[i];list.add(i);}else if (a[i]==max) list.add(i);}for (int i:list){System.out.print((char)(i+'A'));}}
}

最少刷题数

对于一个刷题数量为 a [ i ] 的同学，它增加后的刷题量应该在区间[a[i],100000]为了使得比他刷题多的学生不超过比他刷题少的学生，如果当他刷了 x 道题是符合要求的，那么大于 x 的答案也一定符合，但是小于 x 的答案却不一定符合，这就满足我们的二段性质，因此这道题可以使用二分，用数组cnt[i]统计分数为i的同学有多少位，然后将其变为前缀和数组即可。

import java.io.*;public class Main{static int N = 200010;static int[] a = new int[N], cnt = new int[N];static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));public static void main(String[] args) throws IOException {int n=Integer.parseInt(br.readLine());String[] s = br.readLine().split(" ");for (int i = 0; i < n; i++) {a[i] = Integer.parseInt(s[i]);cnt[a[i]]++;}for (int i = 1; i <= 100000; ++i) {cnt[i] += cnt[i - 1];}for (int i = 0; i < n; ++i) {if (cnt[100000] - cnt[a[i]] <= cnt[Math.max(0,a[i]-1)]) {out.print(0 + " ");continue;}int l = a[i] + 1, r = 100000;while (l < r) {int mid = l + r >> 1;//因为要满足刷题多的人比自己刷题少的人数要小满足就说明mid是答案就更新r=midif (cnt[100000] - cnt[mid] <= cnt[mid - 1] - 1) r = mid;else l = mid + 1;}out.print((r - a[i]) + " ");}out.flush();}
}

求阶乘

二分，由于是阶乘，可知 2 出现的次数一定比 5 多，所以我们只需要看 n ! 能拆分出多少个 5 ，则可知它的阶乘有多少个 0。
最后二分得到的答案还需要判断阶乘末尾0的个数是否恰好为 k 个，因为我们只能保证不少于 k 个，并不一定恰好是 k 个。

import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);long k = sc.nextLong();long l = 1, r = (long) 9e18;while (l < r) {long mid = l + (r - l) / 2;if (query(mid) >= k) r = mid;else l = mid + 1;}long x = query(r);System.out.println(x == k ? r : -1);}static long query(long x) {long ans = 0;while (x > 0) {//不断筛选能拆分出1个 2个3个5的数有多少个，然后累加起来ans += x / 5;x /= 5;}return ans;}
}

import java.util.*;/* 类描述：TODO @author admin* @date 2023-02-21 08:25/public class Main1 {static  int N= 200010;public  static  int [] a =new int [N];public  static  Long [] f = new Long[N];public static int mod = 1000000007;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n =sc.nextInt();for (int i = 1; i <=n; ++i) {a[i]=sc.nextInt();}f[0]=Long.valueOf(1);for (int i = 1; i <=n ; i++) {int mx=a[i],mi=a[i];for (int j = i; j >=1 ; j--) {mx=Math.max(mx,a[j]);mi=Math.min(mi,a[j]);if(mx-mi==i-j){f[i]=(f[i]+f[j-1])%mod;}}}System.out.println(f[n]);}}

1053. 交换一次的先前排列

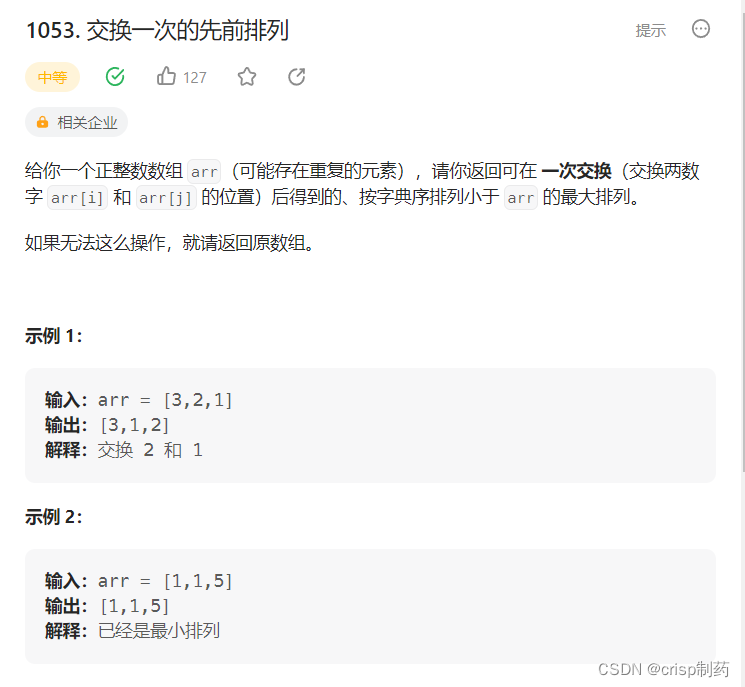
这道题目的关键是 按字典序排列小于 A 的最大可能排列， 那么有
对当前序列进行逆序查找，找到第一个降序的位置 i，使得 A[i]>A[i+1]A[i]>A[i+1]A[i]>A[i+1]
由于 A[i]>A[i+1]A[i]>A[i+1]A[i]>A[i+1]，必能构造比当前字典序小的序列
由于逆序查找，交换 A[i] 为最优解
寻找在 A[i] 最左边且小于 A[i] 的最大的数字 A[j]
由于 A[j]<A[]i]A[j] < A[]i]A[j]<A[]i], 交换 A[i] 与 A[j] 后的序列字典序一定小于当前字典序
由于 A[j] 是满足关系的最大的最左的，因此一定是满足小于关系的交换后字典序最大的

class Solution {public int[] prevPermOpt1(int[] A) {int len = A.length;int curMax = -1;int index = -1;boolean hasResult = false;for (int i = len - 2; i >= 0; i--) {if (A[i+1] < A[i]) {                    // 此处逆序，需要移动A[i]for (int j = i + 1; j < len; j++) { // 寻找与 A[i] 交换的位置if (A[i] > A[j]) {               // 必须满足 A[i] > A[j]，否则不能满足交换后的字典序小于原始字典序hasResult = true;if (A[j] > curMax) {        curMax = A[j];index = j;}} }if (hasResult) {int tmp = A[i];A[i] = A[index];A[index] = tmp;return A;}}}return A;}
}

最大的和

设f[i]是1~i中连续和最大值，g[i]
是i~n中连续和最大值
则答案即max(f[i]+g[i+1]),
1<=i<=n-1
而f[i]怎么求呢，这里一定要细心，不能想当然！！！
以a[i]是否被选为界
1.没被选: f[i-1]即为所求
2.被选： 相当于求1~i中且以a[i]为结尾的连续和最大值

import java.util.*;public class Main {public static  int N=500000;public    static  int []a=new int [N];public  static  int []g = new int [N];public  static  int []f= new int [N];public static void main(String[] args) {Scanner sc = new Scanner(System.in);int t = sc.nextInt();while(t-->0){int n = sc.nextInt();for (int i = 1; i <=n ; i++) {a[i]=sc.nextInt();}int s =0;Arrays.fill(g,-0x3f3f3f3f);Arrays.fill(f,-0x3f3f3f3f);for (int i = 1; i <=n ; i++) {s=Math.max(0,s)+a[i];f[i]=Math.max(f[i-1],s);}s =0;for (int i = n; i >=1; i--) {s=Math.max(0,s)+a[i];g[i]=Math.max(g[i-1],s);}int res =-0x3f3f3f3f;for (int i = 1; i <=n; i++) {res=Math.max(res,f[i]+g[i+1]);}System.out.println(res);}}}