UR5构型机械臂正逆运动学

前言
整理之前的一个项目,当时看着一个博客硬生生计算了差不多一个星期。尝试用MatLab符号推导工具箱化简一部分工作。我使用的大象机器人一款开源入门级协作机器人产品myCobot,开发文档十分完善,但是有部分技术没有开源,如正逆运动学(Forward and inverse kinematics, KF/IK),因此我自己尝试实现了。机器人的具体型号:myCobot 280 M5 2020款。
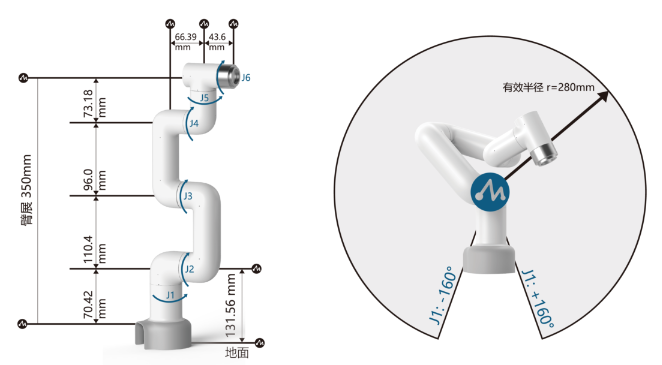
reference
官方文档:https://docs.elephantrobotics.com/docs/gitbook/
UR构型机械臂正逆运动学模型:https://zhuanlan.zhihu.com/p/391202773
6轴机械臂正逆解运算实现:https://blog.csdn.net/weixin_44562141/article/details/108760576
DH参数表
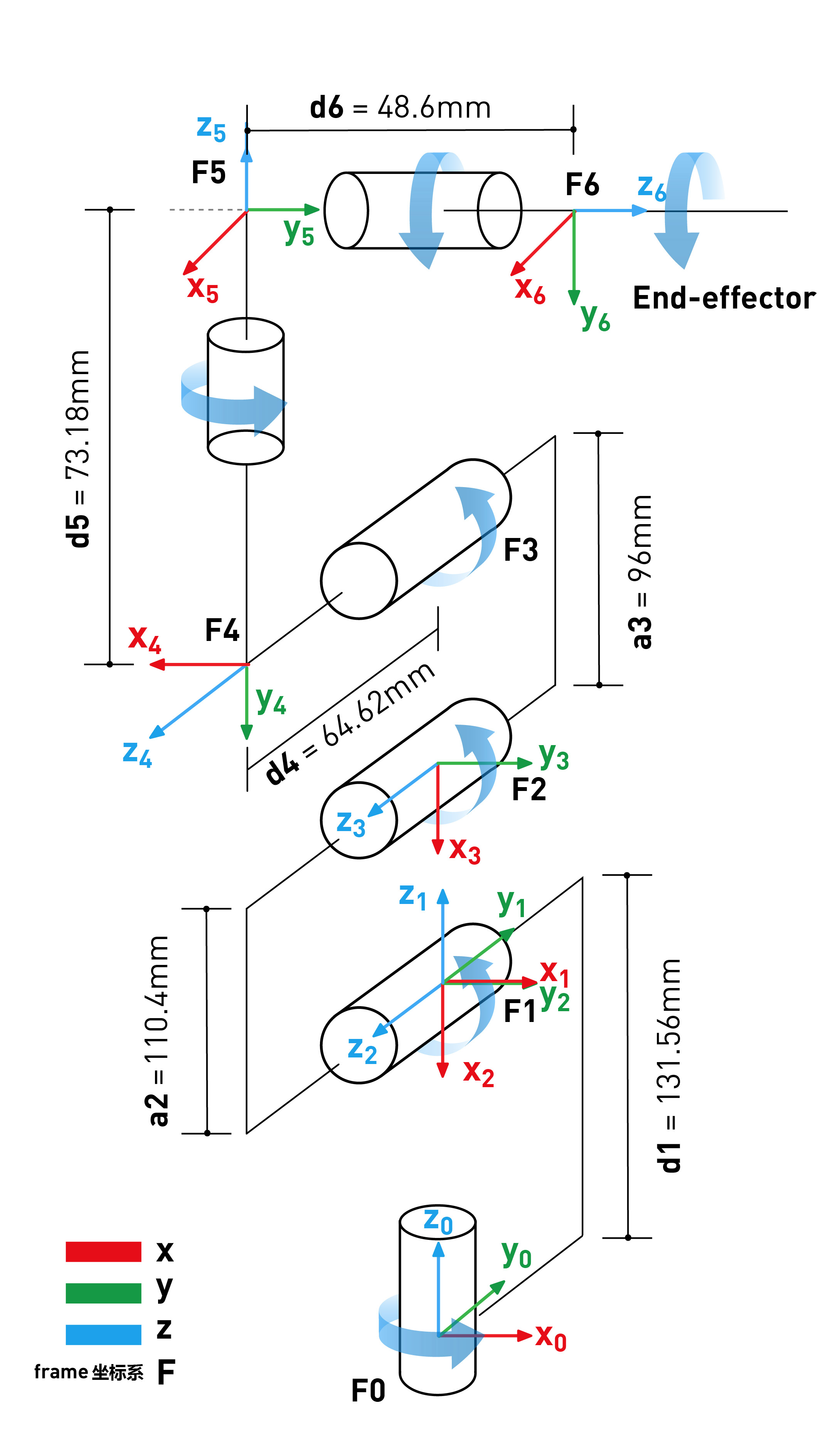
myCobot的DH参数为修正DH参数,串联坐标系之间的变换关系为
- 以
x轴为转轴逆时针(从箭头方向从上往下看)旋转alpha度; - 以
x轴平移长度a; - 以
z轴为转轴逆时针旋转theta+offset度(图中绘制的是theta=0的情形); - 沿
z轴平移长度d(单位为mm);
利用上图信息填写参数表如下
| Joint | alpha | a | d | theta | offset |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 131.56 | theta_1 | 0 |
| 2 | PI/2 | 0 | 0 | theta_2 | -PI/2 |
| 3 | 0 | -110.4 | 0 | theta_3 | 0 |
| 4 | 0 | -96 | 64.62 | theta_4 | -PI/2 |
| 5 | PI/2 | 0 | 73.18 | theta_5 | PI/2 |
| 6 | PI/2 | 0 | 48.6 | theta_6 | 0 |
正运动学
为了将旋转运动与平移运动统一描述,引入齐次坐标系。
以z轴为转轴逆时针旋转theta+offset度,沿z轴平移长度d,对应的变换矩阵为
Rz=[cosθ−sinθ00sinθcosθ00001d0001]R_z=\\begin{bmatrix} cos\\theta & -sin\\theta & 0 & 0\\\\ sin\\theta & cos\\theta & 0 & 0\\\\ 0 & 0 & 1 & d\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix} Rz=cosθsinθ00−sinθcosθ00001000d1
以x轴为转轴逆时针旋转alpha度,以x轴平移长度a,对应的变换矩阵为
Rx=[100a0cosα−sinα00sinαcosα00001]R_x=\\begin{bmatrix} 1 & 0 & 0 & a\\\\ 0 & cos\\alpha & -sin\\alpha & 0\\\\ 0 & sin\\alpha & cos\\alpha & 0\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix} Rx=10000cosαsinα00−sinαcosα0a001
串联坐标系Ti−1T_{i-1}Ti−1与TiT_{i}Ti之间变换描述为
Tii−1=RzRx=[cosθi−sinθi0aicosαisinθicosαisinθi−sinαi−disinαisinαicosθisinαicosθicosαidicosαi0001]T_{i}^{i-1}=R_zR_x= \\begin{bmatrix} cos{\\theta_i} & -sin{\\theta_i} & 0 & a_i\\\\ cos{\\alpha_i}sin{\\theta_i} & cos{\\alpha_i}sin{\\theta_i} & -sin\\alpha_i & -d_isin{\\alpha_i}\\\\ sin{\\alpha_i}cos{\\theta_i} & sin{\\alpha_i}cos{\\theta_i} & cos{\\alpha_i} & d_icos{\\alpha_i}\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix} Tii−1=RzRx=cosθicosαisinθisinαicosθi0−sinθicosαisinθisinαicosθi00−sinαicosαi0ai−disinαidicosαi1
因为对x轴变换在先,将RxR_xRx放在右侧。这个矩阵可以描述如何将坐标系Ti−1T_{i-1}Ti−1变换为TiT_iTi,也可以描述将在TiT_iTi中的坐标点变换到Ti−1T_{i-1}Ti−1中,即在坐标系下的表示。
将DH参数表代入上面的变换矩阵,写出每个Tii−1T_{i}^{i-1}Tii−1变换矩阵
(符号简化表达:cosθi=ci,sinθi=si,sin(θ1+θ2)=s12,cos(θ1+θ2)=c12cos\\theta_i=c_i,sin\\theta_i=s_i,sin(\\theta_1+\\theta_2)=s_{12},cos(\\theta_1+\\theta_2)=c_{12}cosθi=ci,sinθi=si,sin(θ1+θ2)=s12,cos(θ1+θ2)=c12,以此类推)
T10=[c1−s100s1c100001d10001]T21=[c2−s20000−10s2c2000001]T32=[c3−s30a3s3c30000100001]T43=[c4−s40a4s4c400001d40001]T54=[c5−s50000−1−d5s5c5100001]T65=[c6−s600001−d6−s6−c6000001]T_{1}^{0}=\\begin{bmatrix} c_1 & -s_1 & 0 & 0\\\\ s_1 & c_1 & 0 & 0\\\\ 0 & 0 & 1 & d_1\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ T_{2}^{1}=\\begin{bmatrix} c_2 & -s_2 & 0 & 0\\\\ 0 & 0 & -1 & 0\\\\ s_2 & c_2 & 0 & 0\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ T_{3}^{2}=\\begin{bmatrix} c_3 & -s_3 & 0 & a_3\\\\ s_3 & c_3 & 0 & 0\\\\ 0 & 0 & 1 & 0\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ T_{4}^{3}=\\begin{bmatrix} c_4 & -s_4 & 0 & a_4\\\\ s_4 & c_4 & 0 & 0\\\\ 0 & 0 & 1 & d_4\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ T_{5}^{4}=\\begin{bmatrix} c_5 & -s_5 & 0 & 0\\\\ 0 & 0 & -1 & -d_5\\\\ s_5 & c_5 & 1 & 0\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ T_{6}^{5}=\\begin{bmatrix} c_6 & -s_6 & 0 & 0\\\\ 0 & 0 & 1 & -d_6\\\\ -s_6 & -c_6 & 0 & 0\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ T10=c1s100−s1c100001000d11T21=c20s20−s20c200−1000001T32=c3s300−s3c3000010a3001T43=c4s400−s4c4000010a40d41T54=c50s50−s50c500−1100−d501T65=c60−s60−s60−c6001000−d601
在知道每个电机的转角θi\\theta_iθi的情况下,每个矩阵是确定的。这里设末端位姿在T6T_6T6坐标系下的表示为单位矩阵,因此,末端在世界坐标系下的表示为
T60=T10T21T32T43T54T65IT^{0}_{6}=T_{1}^{0}T_{2}^{1}T_{3}^{2}T_{4}^{3}T_{5}^{4}T_{6}^{5}I T60=T10T21T32T43T54T65I
至此,求出机械臂末端在T0T_0T0坐标系(通常设为世界坐标系)下的表示,完成机械臂正运动学的求解。
逆运动学
现已知末端的位姿矩阵,但θi\\theta_iθi未知,因而上面Ti−1iT_{i-1}^{i}Ti−1i矩阵不确定,得到下面等式
T60=T10T21T32T43T54T65=[nxoxaxpxnyoyaypynzozazpz0001]T^{0}_{6}=T_{1}^{0}T_{2}^{1}T_{3}^{2}T_{4}^{3}T_{5}^{4}T_{6}^{5} =\\begin{bmatrix} n_x & o_x & a_x & p_x\\\\ n_y & o_y & a_y & p_y\\\\ n_z & o_z & a_z & p_z\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ T60=T10T21T32T43T54T65=nxnynz0oxoyoz0axayaz0pxpypz1
左右乘以T10T_{1}^{0}T10的逆,得
T61=T21T32T43T54T65=[c1s100−s1c100001−d10001][nxoxaxpxnyoyaypynzozazpz0001]=[c234c5c6−s234s6c234c5s6−s234c6−c234s5a4c23+a3c2+d5s234−d6c234s5−s5c6s5s6−c5−d6c5−d4s234c5c6+c234s6c234s6−s234c5c6−s234s5a4s23+a3s2−d5c234−d6s234s50001]T^{1}_{6}=T_{2}^{1}T_{3}^{2}T_{4}^{3}T_{5}^{4}T_{6}^{5} =\\begin{bmatrix} c_1 & s_1 & 0 & 0\\\\ -s_1 & c_1 & 0 & 0\\\\ 0 & 0 & 1 & -d_1\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix} \\begin{bmatrix} n_x & o_x & a_x & p_x\\\\ n_y & o_y & a_y & p_y\\\\ n_z & o_z & a_z & p_z\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ =\\begin{bmatrix} c_{234}c_5c_6-s_{234}s_6 & c_{234}c_5s_6-s_{234}c_6 & -c_{234}s_5 & a_4c_{23}+a_3c_2+d_5s_{234}-d_6c_{234}s_{5}\\\\ -s_5c_6 & s_5s_6 & -c_5 & -d_6c_5-d_4\\\\ s_{234}c_5c_6+c_{234}s_6 & c_{234}s_6-s_{234}c_5c_6 & -s_{234}s_5 & a_{4}s_{23}+a_3s_2-d_5c_{234}-d_{6}s_{234}s_5\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix} T61=T21T32T43T54T65=c1−s100s1c100001000−d11nxnynz0oxoyoz0axayaz0pxpypz1=c234c5c6−s234s6−s5c6s234c5c6+c234s60c234c5s6−s234c6s5s6c234s6−s234c5c60−c234s5−c5−s234s50a4c23+a3c2+d5s234−d6c234s5−d6c5−d4a4s23+a3s2−d5c234−d6s234s51
这里d6d_6d6这一项是末端坐标系的z向偏移,可以和末端执行器一起考虑(这个机械臂配了一个夹爪,在运动学建模中最后也是一个z向偏移),设其长度为lll,左乘该变换矩阵的逆,得到
[nxoxaxpx′nyoyaypy′nzozazpz′0001]=[nxoxaxpx−ax(d6+l)nyoyaypy−ay(d6+l)nzozazpz−az(d6+l)0001]\\begin{bmatrix} n_x & o_x & a_x & p_x'\\\\ n_y & o_y & a_y & p_y'\\\\ n_z & o_z & a_z & p_z'\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ =\\begin{bmatrix} n_x & o_x & a_x & p_x-a_x(d_6+l)\\\\ n_y & o_y & a_y & p_y-a_y(d_6+l)\\\\ n_z & o_z & a_z & p_z-a_z(d_6+l)\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ nxnynz0oxoyoz0axayaz0px′py′pz′1=nxnynz0oxoyoz0axayaz0px−ax(d6+l)py−ay(d6+l)pz−az(d6+l)1
这样原先的d6d_6d6一项可以置为0得到
[c1s100−s1c100001−d10001][nxoxaxpx′nyoyaypy′nzozazpz′0001]=[c234c5c6−s234s6c234c5s6−s234c6−c234s5a4c23+a3c2+d5s234−s5c6s5s6−c5−d4s234c5c6+c234s6c234s6−s234c5c6−s234s5a4s23+a3s2−d5c2340001]\\begin{bmatrix} c_1 & s_1 & 0 & 0\\\\ -s_1 & c_1 & 0 & 0\\\\ 0 & 0 & 1 & -d_1\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix} \\begin{bmatrix} n_x & o_x & a_x & p_x'\\\\ n_y & o_y & a_y & p_y'\\\\ n_z & o_z & a_z & p_z'\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix}\\\\ =\\begin{bmatrix} c_{234}c_5c_6-s_{234}s_6 & c_{234}c_5s_6-s_{234}c_6 & -c_{234}s_5 & a_4c_{23}+a_3c_2+d_5s_{234}\\\\ -s_5c_6 & s_5s_6 & -c_5 & -d_4\\\\ s_{234}c_5c_6+c_{234}s_6 & c_{234}s_6-s_{234}c_5c_6 & -s_{234}s_5 & a_{4}s_{23}+a_3s_2-d_5c_{234}\\\\ 0 & 0 & 0 & 1\\\\ \\end{bmatrix} c1−s100s1c100001000−d11nxnynz0oxoyoz0axayaz0px′py′pz′1=c234c5c6−s234s6−s5c6s234c5c6+c234s60c234c5s6−s234c6s5s6c234s6−s234c5c60−c234s5−c5−s234s50a4c23+a3c2+d5s234−d4a4s23+a3s2−d5c2341
由矩阵两边(2,4)位置对应相等得
−s1px+c1py=−d4θ1=atan2(py,px)−atan2(−d4,±px2+py2−d42)-s_{1}p_x+c_1p_y=-d_4\\\\ \\theta_1=atan2(p_y,p_x)-atan2(-d_4,\\pm\\sqrt{p_x^2+p_y^2-d_4^2}) −s1px+c1py=−d4θ1=atan2(py,px)−atan2(−d4,±px2+py2−d42)
求解:asinθ+bcosθ=casin\\theta+bcos\\theta=casinθ+bcosθ=c
利用和角公式得a2+b2cos(θ−β)=c\\sqrt{a^2+b^2}cos(\\theta-\\beta)=ca2+b2cos(θ−β)=c
其中b=cosβ,a=sinβb=cos\\beta,a=sin\\betab=cosβ,a=sinβ
代入1+tan2θ=1cos2θ1+tan^2\\theta=\\frac{1}{cos^2\\theta}1+tan2θ=cos2θ1得
tan(θ−β)=±a2+b2−c2ctan(\\theta-\\beta)=\\pm\\frac{\\sqrt{a^2+b^2-c^2}}{c}tan(θ−β)=±ca2+b2−c2
tan(π2−θ+β)=±ca2+b2−c2tan(\\frac{\\pi}{2}-\\theta+\\beta)=\\pm\\frac{c}{\\sqrt{a^2+b^2-c^2}}tan(2π−θ+β)=±a2+b2−c2c
π2−θ+β=atan2(c,±a2+b2−c2)\\frac{\\pi}{2}-\\theta+\\beta=atan2(c,\\pm\\sqrt{a^2+b^2-c^2})2π−θ+β=atan2(c,±a2+b2−c2)
由于b=cosβ=sin(π2+β),a=sinβ=−cos(π2+β)b=cos\\beta=sin(\\frac{\\pi}{2}+\\beta),a=sin\\beta=-cos(\\frac{\\pi}{2}+\\beta)b=cosβ=sin(2π+β),a=sinβ=−cos(2π+β)
θ=atan2(b,−a)−atan2(c,±a2+b2−c2)\\theta=atan2(b,-a)-atan2(c,\\pm\\sqrt{a^2+b^2-c^2})θ=atan2(b,−a)−atan2(c,±a2+b2−c2)
(2,1),(2,2),(2,4)等式:
−s1nx+c1ny=−s5c6(5)−s1ox+c1oy=s5s6(6)−s1ax+c1ay=−c5(7)-s_1n_x+c_1n_y=-s_5c_6 (5)\\\\ -s_1o_x+c_1o_y=s_5s_6 (6)\\\\ -s_1a_x+c_1a_y=-c_5 (7) −s1nx+c1ny=−s5c6(5)−s1ox+c1oy=s5s6(6)−s1ax+c1ay=−c5(7)
由(5)(6)式得
s5=±(−s1nx+c1ny)2+(−s1ox+c1oy)2(8)s_5=\\pm\\sqrt{(-s_1n_x+c_1n_y)^2+(-s_1o_x+c_1o_y)^2} (8) s5=±(−s1nx+c1ny)2+(−s1ox+c1oy)2(8)
由(7)(8)得
θ5=atan2(s5,s1ax−c1ay)\\theta_5=atan2(s_5,s_1a_x-c_1a_y) θ5=atan2(s5,s1ax−c1ay)
当s5≠0s_5\\neq0s5=0时,由(5)(6)式得
θ6=atan2(−s1ox+c1oys5,s1nx−c1nys5)\\theta_6=atan2(\\frac{-s_1o_x+c_1o_y}{s_5},\\frac{s_1n_x-c_1n_y}{s_5}) θ6=atan2(s5−s1ox+c1oy,s5s1nx−c1ny)
当s5=0s_5=0s5=0,即θ5=0,π\\theta_5=0,\\piθ5=0,π时,此时机械臂机构发生奇异,无法求出θ6\\theta_6θ6。
得到θ1,θ5,θ6\\theta_1,\\theta_5,\\theta_6θ1,θ5,θ6之后,剩余的三个关节均在一个平面转动,问题退化为二维。
(1,3),(3,3)等式:
az=−s234s5c1ax+s1ay=−c234s5a_z=-s_{234}s_5\\\\ c_1a_x+s_1a_y=-c_{234}s_5 az=−s234s5c1ax+s1ay=−c234s5
将两式相除得到
θ234=atan2(−azs5,−c1ax+s1ays5)\\theta_{234}=atan2(-\\frac{a_z}{s_5},-\\frac{c_1a_x+s_1a_y}{s_5}) θ234=atan2(−s5az,−s5c1ax+s1ay)
(1,4),(3,4)等式:
c1px+s1py=a4c23+a3c2+d5s234(13)pz−d1=a4s23+a3s2−d5c234(14)c_1p_x+s_1p_y=a_4c_{23}+a_3c_2+d_5s_{234} (13)\\\\ p_z-d_1=a_4s_{23}+a_3s_2-d_5c_{234} (14) c1px+s1py=a4c23+a3c2+d5s234(13)pz−d1=a4s23+a3s2−d5c234(14)
消去θ23\\theta_{23}θ23得
−As2+Bc2=C-As_2+Bc_2=C −As2+Bc2=C
其中,
A=2B2a3B=2B1a3C=B12+B22+a32−a42B1=c1px+s1py−d5s234B2=pz−d1+d5c234A=2B_2a_3\\\\ B=2B_1a_3\\\\ C=B_1^2+B_2^2+a_3^2-a_4^2\\\\ B_1=c_1p_x+s_1p_y-d_5s_{234}\\\\ B_2=p_z-d_1+d_5c_{234} A=2B2a3B=2B1a3C=B12+B22+a32−a42B1=c1px+s1py−d5s234B2=pz−d1+d5c234
从而得到
θ2=atan2(B,A)−atan2(C,±A2+B2−C2)\\theta_2=atan2(B,A)-atan2(C,\\pm\\sqrt{A^2+B^2-C_2}) θ2=atan2(B,A)−atan2(C,±A2+B2−C2)
将θ1,θ2,θ234\\theta_1,\\theta_2,\\theta_{234}θ1,θ2,θ234代入(13)(14)得
s23=B2−a3s2a4c23=B1−a3c2a4s_{23}=\\frac{B_2-a_3s_2}{a_4}\\\\ c_{23}=\\frac{B_1-a_3c_2}{a_4} s23=a4B2−a3s2c23=a4B1−a3c2
进而可得
θ23=atan2(B2−a3s2a4,B1−a3c2a4)θ3=θ23−θ2θ4=θ234−θ23\\theta_{23}=atan2(\\frac{B_2-a_3s_2}{a_4},\\frac{B_1-a_3c_2}{a_4})\\\\ \\theta_3=\\theta_{23}-\\theta_2\\\\ \\theta_4=\\theta_{234}-\\theta_{23} θ23=atan2(a4B2−a3s2,a4B1−a3c2)θ3=θ23−θ2θ4=θ234−θ23
至此,求出了6个关节的转角,一共有8组解。对于简单任务如抓取可以任取一组可行解;但是,对于一些如路径规划类任务需要考虑与当前状态“相近”的解,机械臂可以以最小成本完成动作到达目标位姿。
