求三维坐标系的旋转矩阵通常需要求分别沿3个坐标轴的二维坐标系下的旋转矩阵，二维坐标系下的旋转矩阵的推导过程通常以某一点逆时针旋转$\theta$角度进行推理。以下将通过此例来详细讲解二维坐标系下的旋转矩阵推导过程，并进一步给出其他方式的旋转矩阵。

一、二维坐标中点的旋转变换

点的旋转矩阵（逆时针旋转）

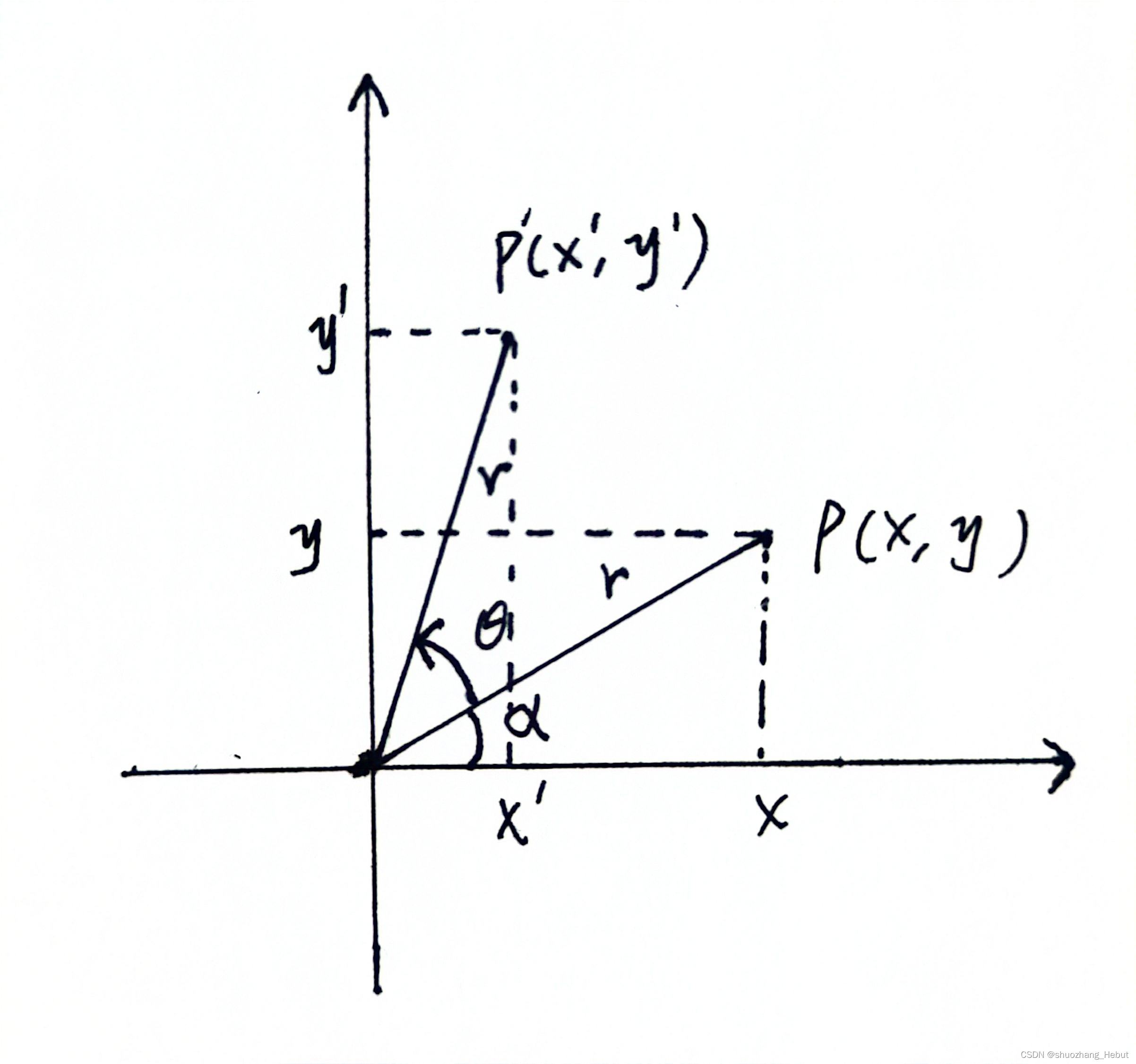
已知点$P(x,y)$，将该点以逆时针方向旋转$\theta$角度后得到点P′(x′,y′)P^{\\prime}(x^{\\prime}, y^{\\prime})P′(x′,y′)，如下图所示。求由点$P$到点P′P^{\\prime}P′的旋转矩阵。

• 设半径为$r$，由图可以分别得到以下三角公式：

  • 对于点$P(x,y)$
    x=rcos⁡αy=rsin⁡α(1)\\begin{aligned} & x=r \\cos \\alpha \\\\ & y=r \\sin \\alpha \\end{aligned} \\tag{1}​x=rcosαy=rsinα​(1)
  • 对于点P′(x′,y′)P^{\\prime}(x^{\\prime}, y^{\\prime})P′(x′,y′)
    x′=rcos⁡(α+θ)y′=rsin⁡(α+θ)(2)\\begin{aligned} & x^{\\prime}=r \\cos (\\alpha+\\theta) \\\\ & y^{\\prime}=r \\sin (\\alpha+\\theta) \\end{aligned} \\tag{2}​x′=rcos(α+θ)y′=rsin(α+θ)​(2)

• 根据两角和的正弦与余弦公式：
  sin⁡(α+θ)=sin⁡αcos⁡θ+cos⁡αsin⁡θcos⁡(α+θ)=cos⁡αcos⁡θ−sin⁡αsin⁡θ(3)\\begin{aligned} & \\sin (\\alpha+\\theta)=\\sin \\alpha \\cos \\theta+\\cos \\alpha \\sin \\theta \\\\ & \\cos (\\alpha+\\theta)=\\cos \\alpha \\cos \\theta-\\sin \\alpha \\sin \\theta \\end{aligned} \\tag{3} ​sin(α+θ)=sinαcosθ+cosαsinθcos(α+θ)=cosαcosθ−sinαsinθ​(3)

• 将公式(3)代入公式(2)，可得到：
  x′=rcos⁡αcos⁡θ−rsin⁡αsin⁡θy′=rsin⁡αcos⁡θ+rcos⁡αsin⁡θ(4)\\begin{aligned} & x^{\\prime} =r \\cos \\alpha \\cos \\theta-r \\sin \\alpha \\sin \\theta \\\\ & y^{\\prime} =r \\sin \\alpha \\cos \\theta+r \\cos \\alpha \\sin \\theta \\\\ \\end{aligned} \\tag{4} ​x′=rcosαcosθ−rsinαsinθy′=rsinαcosθ+rcosαsinθ​(4)

• 将公式(1)代入公式(4)，化简掉$\alpha$，可得到(x′,y′)(x^{\\prime}, y^{\\prime})(x′,y′)与$(x,y)$的关系，即：
  x′=xcos⁡θ−ysin⁡θy′=ycos⁡θ+xsin⁡θ(5)\\begin{aligned} & x^{\\prime} =x \\cos \\theta-y \\sin \\theta \\\\ & y^{\\prime} =y \\cos \\theta+x \\sin \\theta \\\\ \\end{aligned} \\tag{5} ​x′=xcosθ−ysinθy′=ycosθ+xsinθ​(5)

• 整理公式(5)可得到旋转矩阵公式：
  x′=cos⁡θ⋅x−sin⁡θ⋅yy′=sin⁡θ⋅x+cos⁡θ⋅y⇒[x′y′]=[cos⁡θ−sin⁡θsin⁡θcos⁡θ][xy](6)\\begin{aligned} x^{\\prime}&=\\cos \\theta \\cdot x-\\sin \\theta \\cdot y \\\\ y^{\\prime}&=\\sin \\theta \\cdot x+\\cos \\theta \\cdot y \\\\ \\Rightarrow \\left[\\begin{array}{l} x^{\\prime} \\\\ y^{\\prime}\\end{array}\\right] &=\\left[\\begin{array}{cc}\\cos \\theta & -\\sin \\theta \\\\ \\sin \\theta & \\cos \\theta \\end{array}\\right] \\left[\\begin{array}{l} x \\\\ y \\end{array}\\right] \\end{aligned} \\tag{6} x′y′⇒[x′y′​]​=cosθ⋅x−sinθ⋅y=sinθ⋅x+cosθ⋅y=[cosθsinθ​−sinθcosθ​][xy​]​(6)

• 因此二维坐标系下逆时针旋转矩阵$R$为：
  R=[cos⁡θ−sin⁡θsin⁡θcos⁡θ]R = \\left[\\begin{array}{cc}\\cos \\theta & -\\sin \\theta \\\\ \\sin \\theta & \\cos \\theta \\end{array}\\right] R=[cosθsinθ​−sinθcosθ​]

点的旋转矩阵（顺时针旋转）

已知点P′(x′,y′)P^{\\prime}(x^{\\prime}, y^{\\prime})P′(x′,y′)，将该点以顺时针方向旋转$\theta$角度后得到点$P(x,y)$，求$P$。

1、利用求逆矩阵的方式

• 二阶矩阵的逆的求法为：主对角元素换位置,次对角元素变符号，再乘上系数1/(ad-bc)，由于旋转矩阵$R$的ad-bc=1，因此$R$的逆矩阵R′R^{\\prime}R′为：
  R′=[cos⁡θsin⁡θ−sin⁡θcos⁡θ]R^{\\prime} = \\left[\\begin{array}{cc}\\cos \\theta & \\sin \\theta \\\\ -\\sin \\theta & \\cos \\theta \\end{array}\\right] R′=[cosθ−sinθ​sinθcosθ​]
• 因此旋转公式为：
  [xy]=[cos⁡θsin⁡θ−sin⁡θcos⁡θ][x′y′]\\left[\\begin{array}{l} x \\\\ y \\end{array}\\right] = \\left[\\begin{array}{cc}\\cos \\theta & \\sin \\theta \\\\ -\\sin \\theta & \\cos \\theta \\end{array}\\right] \\left[\\begin{array}{l} x^{\\prime} \\\\ y^{\\prime}\\end{array}\\right] [xy​]=[cosθ−sinθ​sinθcosθ​][x′y′​]

2、利用几何知识推导

将P′P^{\\prime}P′顺时针旋转$\theta$角度到$P$，相当于逆时针旋转$(2\pi -\theta )$，由于三角函数的周期为$2\pi$，因此相当于旋转$-\theta$角度。

• 将$-\theta$代入到公式(6)，得到：
  x=cos⁡(−θ)⋅x′−sin⁡(−θ)⋅y′=cos⁡θ⋅x′+sin⁡θ⋅y′y=sin⁡(−θ)⋅x′+cos⁡(−θ)⋅y′=−sin⁡θ⋅x′+cos⁡θ⋅y′\\begin{aligned} x & =\\cos (-\\theta) \\cdot x^{\\prime}-\\sin (-\\theta) \\cdot y^{\\prime} \\\\ & =\\cos \\theta \\cdot x^{\\prime}+\\sin \\theta \\cdot y^{\\prime} \\\\ y & =\\sin (-\\theta) \\cdot x^{\\prime}+\\cos (-\\theta) \\cdot y^{\\prime} \\\\ & =-\\sin \\theta \\cdot x^{\\prime}+\\cos \\theta \\cdot y^{\\prime} \\end{aligned} xy​=cos(−θ)⋅x′−sin(−θ)⋅y′=cosθ⋅x′+sinθ⋅y′=sin(−θ)⋅x′+cos(−θ)⋅y′=−sinθ⋅x′+cosθ⋅y′​
• 整理上述公式可得到顺时针时的旋转矩阵公式：
  x=cos⁡θ⋅x′+sin⁡θ⋅y′y=−sin⁡θ⋅x′+cos⁡θ⋅y′⇒[xy]=[cos⁡θsin⁡θ−sin⁡θcos⁡θ][x′y′]\\begin{aligned} x&=\\cos \\theta \\cdot x^{\\prime}+\\sin \\theta \\cdot y^{\\prime} \\\\ y&=-\\sin \\theta \\cdot x^{\\prime}+\\cos \\theta \\cdot y^{\\prime} \\\\ \\Rightarrow \\left[\\begin{array}{l} x \\\\ y \\end{array}\\right] &= \\left[\\begin{array}{cc}\\cos \\theta & \\sin \\theta \\\\ -\\sin \\theta & \\cos \\theta \\end{array}\\right] \\left[\\begin{array}{l} x^{\\prime} \\\\ y^{\\prime}\\end{array}\\right] \\end{aligned} xy⇒[xy​]​=cosθ⋅x′+sinθ⋅y′=−sinθ⋅x′+cosθ⋅y′=[cosθ−sinθ​sinθcosθ​][x′y′​]​

二、二维坐标系的旋转变换

二维坐标系$\text{XOY}$中有一点$P(x,y)$，将坐标系$\text{XOY}$逆时针旋转$\theta$角度后得到新坐标系X′O′Y′\\text{X}^{\\prime}\\text{O}^{\\prime}\\text{Y}^{\\prime}X′O′Y′，求点$P$在新坐标系下的坐标P′(x′,y′)P^{\\prime}(x^{\\prime}, y^{\\prime})P′(x′,y′)，这个过程称为坐标系变换。

新坐标的求法可以转换为逆向旋转坐标点的方式，并利用点的旋转变换求得。因此，坐标系顺时针旋转$\theta$角度，相当于原坐标系中某一点逆时针旋转$\theta$角度，反之亦然。

总结

• 某点逆时针旋转$\theta$角度（坐标系顺时针旋转$\theta$角度）的旋转矩阵为：
  R=[cos⁡θ−sin⁡θsin⁡θcos⁡θ]R = \\left[\\begin{array}{cc}\\cos \\theta & -\\sin \\theta \\\\ \\sin \\theta & \\cos \\theta \\end{array}\\right] R=[cosθsinθ​−sinθcosθ​]
• 某点顺时针旋转$\theta$角度（坐标系逆时针旋转$\theta$角度）的旋转矩阵为：
  R′=[cos⁡θsin⁡θ−sin⁡θcos⁡θ]R^{\\prime} = \\left[\\begin{array}{cc}\\cos \\theta & \\sin \\theta \\\\ -\\sin \\theta & \\cos \\theta \\end{array}\\right] R′=[cosθ−sinθ​sinθcosθ​]
  三维坐标变换可进一步参考Link3。

参考：
Link1
Link2
Link3