注意下面所有$w$表示的都是角速度而不是频率

电压有效值

高中物理中知道有效值电压是根据电阻发热的功率等效得到的
对于正弦波的电压，U=UmsinwtU=U_{m}sinwtU=Um​sinwt,对应的电流I=UmRsinwtI=\\frac{U_{m}}{R}sinwtI=RUm​​sinwt
求得一个周期的发热量
∫0TI2Rdt=∫0T(Umsinwt)2Rdt=Um2R∫0T(sinwt)2dt(公式1)\\int_0^TI^2Rd_t=\\int_0^T\\frac{{({U_m}sinwt})^2}Rd_t=\\frac{U_m^2}{R}\\int_0^T(sinwt)^2d_t \\tag{公式1} ∫0T​I2Rdt​=∫0T​R(Um​sinwt)2​dt​=RUm2​​∫0T​(sinwt)2dt​(公式1)
公式1中的可以化简如下,
∫0T(sinwt)2dt=∫0T1−cos2wt2dt=∫0T12dt−∫0Tcos2wt2dt⇒余弦函数周期内积分0=∫0T12dt=T2\\int_0^T(sinwt)^2d_t =\\int_0^T\\frac{1-cos2wt}{2}d_t =\\int_0^T\\frac{1}{2}d_t-\\int_0^T\\frac{cos2wt}{2}d_t \\xRightarrow{余弦函数周期内积分0}=\\int_0^T\\frac{1}{2}d_t=\\frac{T}2 ∫0T​(sinwt)2dt​=∫0T​21−cos2wt​dt​=∫0T​21​dt​−∫0T​2cos2wt​dt​余弦函数周期内积分0​=∫0T​21​dt​=2T​
则公式1最终结果
Um2R∫0T(sinwt)2dt=Um2R.T2=U有效2R.(公式2)\\frac{U_m^2}{R}\\int_0^T(sinwt)^2d_t =\\frac{U_m^2}{R}. \\frac{T}2=\\frac{U_{有效}^2}{R}. \\tag{公式2} RUm2​​∫0T​(sinwt)2dt​=RUm2​​.2T​=RU有效2​​.(公式2)
通过公式2可知
U有效=Um2U_{有效}=\\frac{U_{m}}{\\sqrt{2}} U有效​=2​Um​​

电容电感的电压和电流的相位问题

电容的电流和电压

电流I=dQdt=CdUdt(式子2-1)I=\\frac{dQ}{dt}=\\frac{CdU}{dt}\\tag{式子2-1}I=dtdQ​=dtCdU​(式子2-1)
其中$dQ表示电容上电荷变化量，dU表示电压变化量$
设电压是正弦波的交流电U=UmsinwtU=U_msinwtU=Um​sinwt，再有式子2-1可知电流
I=Cd(Umsinwt)dt=CUmwcoswtI=\\frac{Cd(U_msinwt)}{dt}=CU_mwcoswtI=dtCd(Um​sinwt)​=CUm​wcoswt
通过上面电流和电压的公式可以看出电流比电压超前π2\\LARGE\\frac{\\pi}{2}2π​

电感的电流和电压

设电流值是正弦函数：I=ImsinwtI=I_msinwtI=Im​sinwt，电流和电压的关系如下
U=dΨdt=LdIdt=LImdsinwtdt=LImwcoswtU=\\frac{d\\Psi}{dt}=\\frac{LdI}{dt}=\\frac{LI_mdsinwt}{dt}=LI_mwcoswt U=dtdΨ​=dtLdI​=dtLIm​dsinwt​=LIm​wcoswt
通过上面的电流和电压的表达式可知电压比电流超前π2\\LARGE\\frac{\\pi}{2}2π​

电容的容抗计算公式

f是电容两端的频率，c是电容值

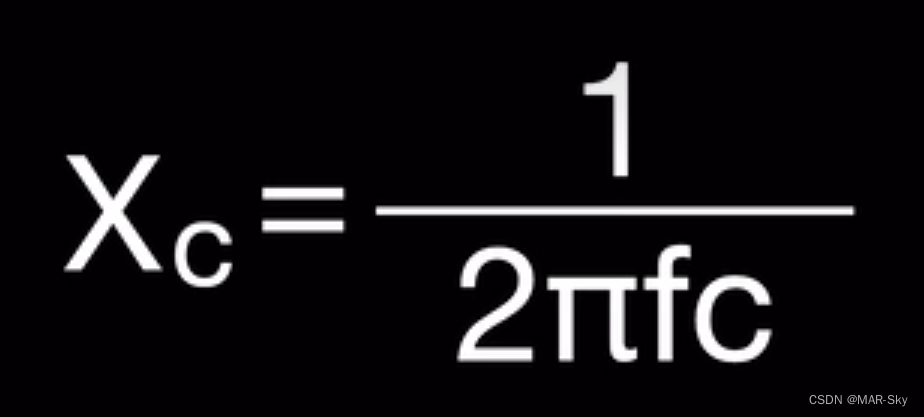
根据电阻的有效电压的思想计算电容的容抗

参考：https://zhuanlan.zhihu.com/p/39915001
首先认为加在电容两端的电压依然认为是正弦波的电压U=Umsinwt(电压)U=U_{m}sinwt \\tag{电压}U=Um​sinwt(电压)
对应电压的有效值是：U有效=Um2(电压有效)U_{有效}=\\frac{U_{m}}{\\sqrt{2}}\\tag{电压有效}U有效​=2​Um​​(电压有效)
电容的电流和电压关系:
I=CdUdt=Cd(Umsinwt)dtI=C\\frac{dU}{dt}=C\\frac{d({U_{m}sinwt })}{dt}I=CdtdU​=Cdtd(Um​sinwt)​
设电容的阻值是XCX_CXC​,那么一个周期内的发热计算
I有效2XCT=∫0TI2XCdt=∫0T(Cd(Umsinwt)dt)2XCdt=∫0TI2XCdt=∫0T(CwUmcoswt)2XCdtI_{有效}^2X_CT=\\int_0^TI^2X_Cdt=\\int_0^T({C\\frac{d({U_{m}sinwt })}{dt}})^2X_Cdt=\\int_0^TI^2X_Cdt=\\int_0^T({Cw{{U_{m}coswt })}}^2X_CdtI有效2​XC​T=∫0T​I2XC​dt=∫0T​(Cdtd(Um​sinwt)​)2XC​dt=∫0T​I2XC​dt=∫0T​(CwUm​coswt)2XC​dt
上式中消去容抗XcX_cXc​可得
I有效2T=∫0T(CwUmcoswt)2dt=(CwUm)2∫0T(coswt)2dt(式3)I_{有效}^2T=\\int_0^T({Cw{{U_{m}coswt })}}^2dt={(CwU_{m})}^2\\int_0^T({{{coswt })}}^2dt\\tag{式3} I有效2​T=∫0T​(CwUm​coswt)2dt=(CwUm​)2∫0T​(coswt)2dt(式3)
式子3中的化简，
(CwUm)2∫0T(coswt)2dt=(CwUm)2∫0T1+cos2wt2dt=(CwUm)2(∫0T12dt+∫0Tcos2wt2dt)⇒余弦函数周期内积分0=(CwUm)2T2(式4)\\begin{aligned} {(CwU_{m})}^2\\int_0^T({{{coswt })}}^2dt &={(CwU_{m})}^2\\int_0^T\\frac{1+cos2wt}{2}dt \\\\ &= {(CwU_{m})}^2(\\int_0^T\\frac{1}{2}d_t+\\int_0^T\\frac{cos2wt}{2}d_t ) \\\\& \\xRightarrow{余弦函数周期内积分0} \\\\&={(CwU_{m})}^2\\frac{T}{2}\\tag{式4} \\end{aligned}(CwUm​)2∫0T​(coswt)2dt​=(CwUm​)2∫0T​21+cos2wt​dt=(CwUm​)2(∫0T​21​dt​+∫0T​2cos2wt​dt​)余弦函数周期内积分0​=(CwUm​)22T​​(式4)
式子3和4可知
I有效2T=(CwUm)2T2I有效=CwUm2(式5)\\begin{aligned} I_{有效}^2T&={(CwU_{m})}^2\\frac{T}{2} \\\\I_{有效}&= \\frac{CwU_{m}}{\\sqrt{}{2}}\\tag{式5} \\end{aligned}I有效2​TI有效​​=(CwUm​)22T​=​2CwUm​​​(式5)
最终容抗值可得
XC=U有效I有效=Um2CwUm2=1Cw=12πfCX_C=\\frac{U_{有效}}{I_{有效}}=\\frac{\\frac{U_m}{\\sqrt{2}}}{\\frac{CwU_{m}}{\\sqrt{}{2}}}=\\frac{1}{Cw}=\\frac{1}{2\\pi fC} XC​=I有效​U有效​​=​2CwUm​​2​Um​​​=Cw1​=2πfC1​

电感感抗

假设电流是：I=Imsin(wt)I=I_msin(wt)I=Im​sin(wt),
根据正弦波得有效值可知道有效电流I有效=Im2I_{有效}=\\frac{I_m}{\\sqrt{2}}I有效​=2​Im​​
对应得电压公式
U=LdIdt=Ld(Imsinwt)dt=wLImcos(wt)U=L\\frac{dI}{dt}=L\\frac{d(I_msinwt)}{dt}=wLI_mcos(wt) U=LdtdI​=Ldtd(Im​sinwt)​=wLIm​cos(wt)
同样设电感得阻值是XLX_LXL​
可知下面的等式
I有效2XLT=∫0T(UXL)2XLdt=(wLIm)2XL∫0T(coswt)2dt=(wLIm)2XL∫0T1+cos2wt2dt=(wLIm)2XL∫0T12dt+0(公式6)\\begin{aligned} {I_{有效}}^2X_LT&=\\int_0^T (\\frac{U}{X_L})^2X_Ldt\\\\&=\\frac{(wLI_m)^2}{X_L}\\int_0^T(coswt)^2dt\\\\&=\\frac{(wLI_m)^2}{X_L}\\int_0^T\\frac{1+cos2wt}{2}dt\\\\&=\\frac{(wLI_m)^2}{X_L}\\int_0^T\\frac{1}{2}dt+0\\tag {公式6} \\end{aligned}I有效​2XL​T​=∫0T​(XL​U​)2XL​dt=XL​(wLIm​)2​∫0T​(coswt)2dt=XL​(wLIm​)2​∫0T​21+cos2wt​dt=XL​(wLIm​)2​∫0T​21​dt+0​(公式6)
公式6可化简为
Im2XLT2=(wLIm)2XLT2⇒两边消去相同得项得到XL=(wL)2XL⇒最后得到电抗XL=wL\\frac{I_m^2X_LT}{2}=\\frac{(wLI_m)^2}{X_L}\\frac{T}{2}\\xRightarrow{两边消去相同得项得到}X_L=\\frac{(wL)^2}{X_L}\\xRightarrow{最后得到电抗}X_L=wL 2Im2​XL​T​=XL​(wLIm​)2​2T​两边消去相同得项得到​XL​=XL​(wL)2​最后得到电抗​XL​=wL