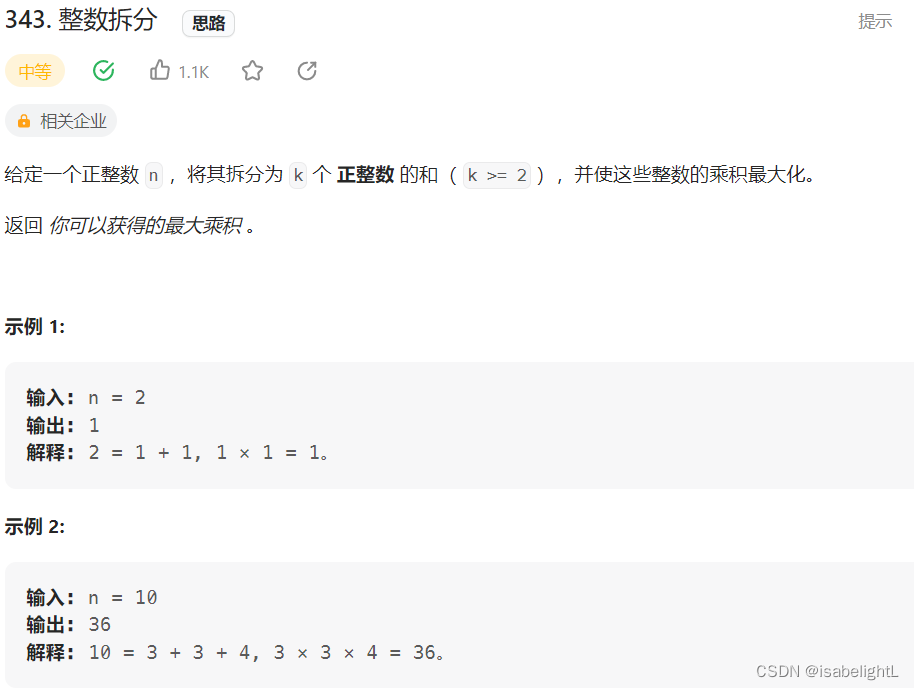
343. 整数拆分

链接：代码随想录

视频讲解很详细，链接动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分_哔哩哔哩_bilibili

 

class Solution {
public:
/*使这些整数的乘积最大化,乘积最大化没有见过，没思路
//看了讲解
dp[i] 意味着对数字i进行拆分后，拆分数的最大值
拆成2个数， j, i-j。 
拆成3个或者3个以上的数，j, dp[i-j](个数未知)初始值,dp[0]----------------对0拆分无意义dp[1]-----------------1*1=1dp[2]-----------------1*2=1dp[3]-----------------1*3 2*dp[1]-------3
*/int integerBreak(int n) {vector<int>dp(n+1,0);dp[2]=1;for(int i=3;i<=n;i++)//拆分2、拆分3、。。。。拆分n{for(int j=1;j<=i/2;j++){dp[i]=max(max(j*(i-j),j*dp[i-j]),dp[i]);}}return dp[n];}
};

 注意：我在这里犯了两个错，有两个不好理解的点，一是更新最大值的时候要跟上一个dp[i]

一、对比更新，所以最后的递推式写出来要比较三个数：

1、拆分成两个数的j*(i-j)

2、拆分成多个数的j*dp[i-j]

3、每一轮终需要更新的dp[i]

二、截取的j，要从1-i/2, 而不是j*j<=i.

反例：

这里按照j<=i/2，j=1,2,3.

按照j*j<=i，j=1,2 

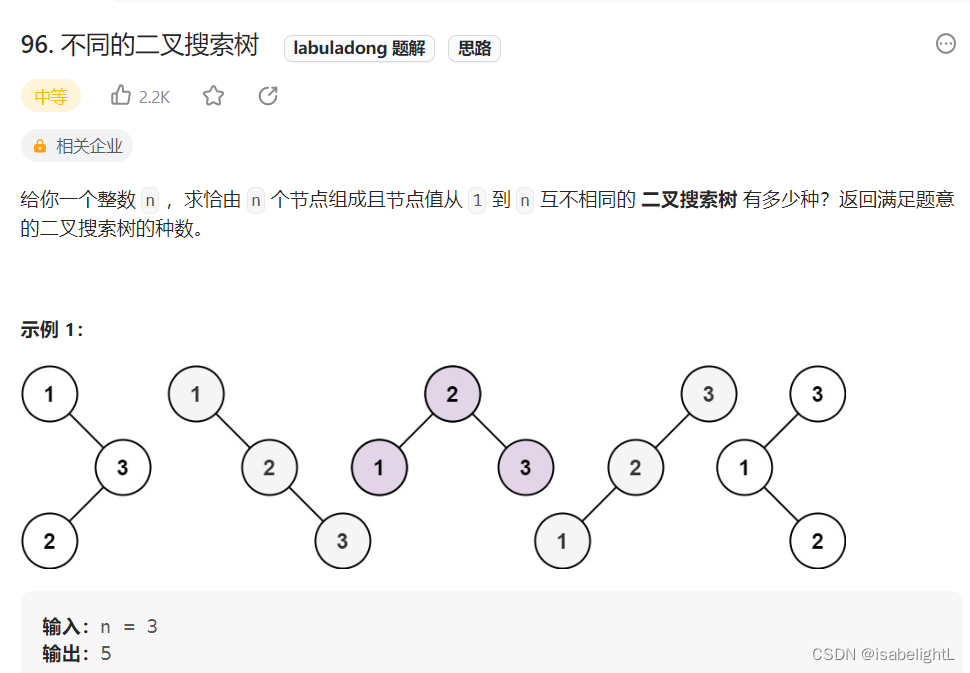
96.不同的二叉搜索树 

链接：代码随想录

 自己实在想了一堆非常废的想法，外加我现在很困很困。。。。呜呜呜昨天应该早点睡，但是睡了又怕起不来。

在卡哥的角度，这道题以n=3为例子进行讲解。

可以看成以1为根节点、以2为根节点、以3为根节点 的 组合。

 

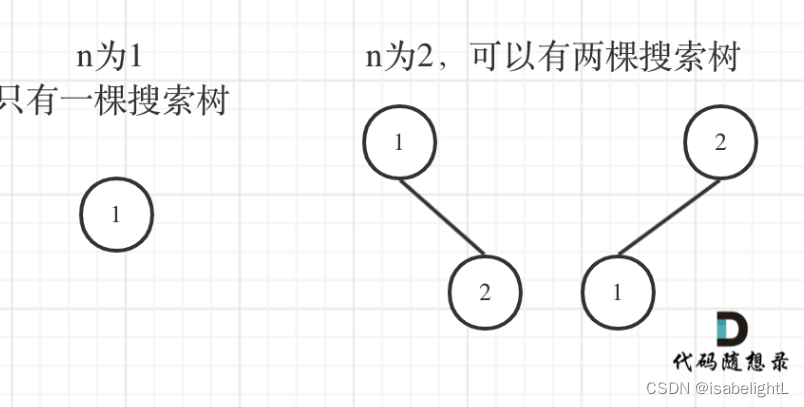
 这道题显然是从0、1、2从小到大推3

dp[i]代表节点个数为i时，树的种类数为dp[i]

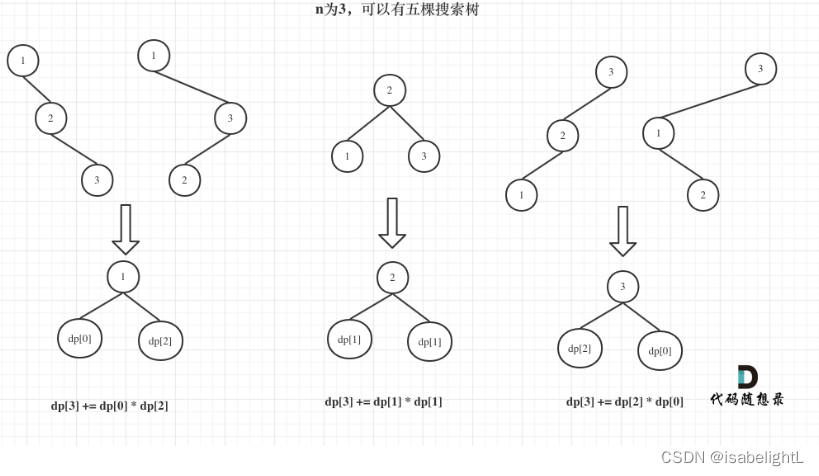
则以j为节点,j左子树的节点为1到j-1,共j-1个；

                    j 右子树的节点为j+1到i,左闭右闭,共i-j个。

即以j为节点，dp[i]=dp[j-1]*dp[i-j]

同时j可以是0、1、2...n,故dp[i]是所有情况的累加。

//动态规划初始值
dp[0]=1;//------------------空树也算是树的一种情况，如果等于0那么乘以任何数都为0了
dp[1]=1;//------------------n=1时dp[1]
dp[2]=2;
for(int i=3;i<=n;i++)
{for(int j=1;j<=i;j++)
{dp[i]+=dp[j-1]*dp[i-j];
}}
return dp[n];

不知道为什么自己写的答案报了overflow(因为如果n=1,根本不可能出现dp[2]，我这算是提前写了dp[2])

正确答案：

class Solution {
public:int numTrees(int n) {vector<int>dp(n+1,0);
//动态规划初始值if(n==0||n==1){return 1;}// n>1，则必定出现dp[0]\\dp[1]dp[0]=1;//------------------空树也算是树的一种情况dp[1]=1;//------------------n=1时dp[1]for(int i=2;i<=n;i++){for(int j=1;j<=i;j++){dp[i]+=dp[j-1]*dp[i-j];}cout<<i<<"   "<<dp[i]<<endl;}return dp[n];}
};