数值方法笔记3:线性和非线性方程组求解

- 前置知识1:矩阵范数
- 前置知识2:舒尔补
- 前置知识3:可约矩阵
- 前置知识4:谱半径
- 1.【线性方程组】直接求解:高斯消元法(LULULU分解)、LDVLDVLDV分解、LDLTLDL^TLDLT分解、UDUTUDU^TUDUT分解
-
- 1.1 高斯消元法(LULULU分解)
- 1.2 LDVLDVLDV分解、LDLTLDL^TLDLT分解、UDUTUDU^TUDUT分解
- 1.3 误差分析(从条件数的角度)
- 2. 【线性方程组】间接迭代求解:Jacobi方法, Gauss-Seidel方法
-
- 2.1 Jacobi方法
- 2.2 Gauss-Seidel方法
- 2.3 Jacobi方法, Gauss-Seidel方法收敛的条件
- 2.4 预测迭代次数
- 2.5 连续超松弛方法(The Method of Successive Over-Relaxation【SOR】)
- 2.6 总结:Jacobi方法, Gauss-Seidel方法对比:
- 2.7 对称矩阵的Gauss-Seidel方法
- 2.8 Krylov方法(Krylov methods)
- 2.9 GMRES方法(Generalized Minimum Residual Method)
- 3. 【线性方程组】基于优化的方法
-
- 3.1 共轭梯度法(Conjugate gradient method【CG】)
- 3.2 共轭梯度法和其他算法的对比
- 3.3 预条件共轭梯度法(Preconditioned conjugate gradient method)
- 4. 【非线性方程组】Jacobian矩阵、Newton迭代法、不动点迭代法、Seidel迭代法
-
- 4.1 Jacobian矩阵
- 4.2 Newton迭代法
- 4.3 不动点迭代法
- 4.4 Seidel迭代法
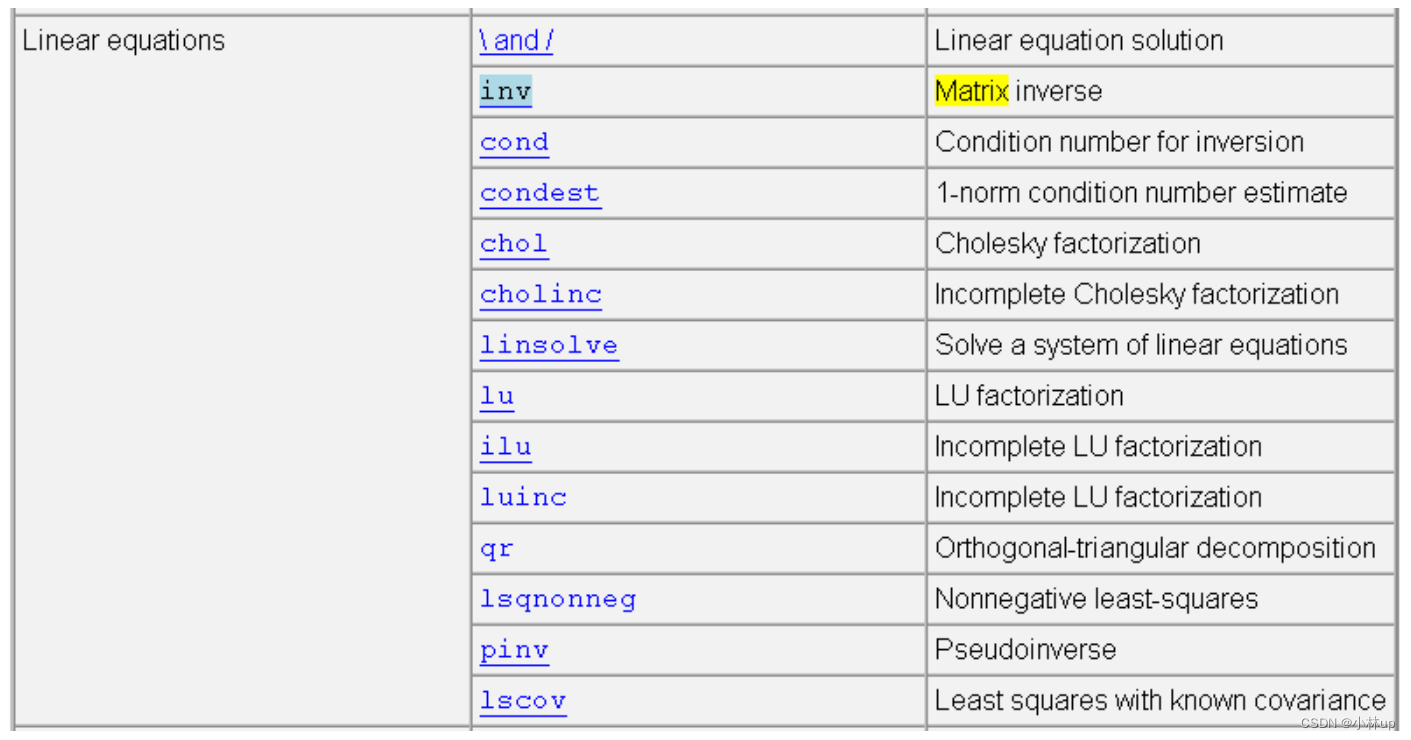
- 5. Matlab相关函数
前置知识1:矩阵范数
矩阵范数的性质:
(1) 若A≠0A \\neq 0A=0 , 那么∥A∥>0\\|A\\|>0∥A∥>0; 若 A=0A=0A=0 , 那么∥A∥=0\\|A\\|=0∥A∥=0 .
(2) 对于α∈R\\alpha \\in \\mathrm{R}α∈R,∥αA∥=∣α∣∥A∥\\|\\alpha A\\|=|\\alpha|\\|A\\|∥αA∥=∣α∣∥A∥ .
(3) ∥A+B∥≤∥A∥+∥B∥\\|A+B\\| \\leq\\|A\\|+\\|B\\|∥A+B∥≤∥A∥+∥B∥.
(4) ∥AB∥≤∥A∥∥B∥\\|A B\\| \\leq\\|A\\|\\|B\\|∥AB∥≤∥A∥∥B∥ .
常见的矩阵范数:
∥A∥=max∥x∥1∥Ax∥∥A∥1=max∥x∥1=1∥Ax∥1=maxk∑i=1n∣aik∣(列和范数)∥A∥2=max∥x∥2=1∥Ax∥2=λ1,λ1是ATA的最大特征值(A的最大奇异值).∥A∥∞=max∣x∥∞=1∥Ax∥∞=maxi∑k=1n∣aik∣(行和范数)∥A∥F=(∑i=1,k=1n∣aik∣2)1/2\\begin{aligned} &\\|A\\|=\\max _{\\|x\\|_{1}}\\|A x\\|\\\\ &\\|A\\|_{1}=\\max _{\\|x\\|_{1}=1}\\|A x\\|_{1}=\\max _{k} \\sum_{i=1}^{n}\\left|a_{i k}\\right| (\\text{列和范数})\\\\ &\\|A\\|_{2}=\\max _{\\|x\\|_{2}=1}\\|A x\\|_{2}=\\sqrt{\\lambda_{1}}, \\lambda_{1} \\text { 是}A^{T} A\\text{的最大特征值(}A\\text{的最大奇异值)} . \\\\ &\\|A\\|_{\\infty}=\\max _{\\mid x \\|_{\\infty}=1}\\|A x\\|_{\\infty}=\\max _{i} \\sum_{k=1}^{n}\\left|a_{i k}\\right| (\\text{行和范数}) \\\\ &\\|A\\|_{F}=\\left(\\sum_{i=1, k=1}^{n}\\left|a_{i k}\\right|^{2}\\right)^{1 / 2} \\quad \\end{aligned}∥A∥=∥x∥1max∥Ax∥∥A∥1=∥x∥1=1max∥Ax∥1=kmaxi=1∑n∣aik∣(列和范数)∥A∥2=∥x∥2=1max∥Ax∥2=λ1,λ1 是ATA的最大特征值(A的最大奇异值).∥A∥∞=∣x∥∞=1max∥Ax∥∞=imaxk=1∑n∣aik∣(行和范数)∥A∥F=i=1,k=1∑n∣aik∣21/2
而对于向量范数:
∥x∥p=(∑k=1n∣xk∣p)1/p\\|x\\|_{p}=\\left(\\sum_{k=1}^{n}\\left|x_{k}\\right|^{p}\\right)^{1 / p}∥x∥p=(k=1∑n∣xk∣p)1/p
范数∥∗∥a\\|\\ast\\|_a∥∗∥a和范数∥∗∥b\\|\\ast\\|_b∥∗∥b等价:
c1∥A∥a≤∥A∥b≤c2∥A∥ac1′∥A∥b≤∥A∥a≤c2∥A∥b\\begin{aligned} c_{1}\\|A\\|_{a} \\leq\\|A\\|_{b} \\leq c_{2}\\|A\\|_{a} \\\\ c_{1}^{\\prime}\\|A\\|_{b} \\leq\\|A\\|_{a} \\leq c_{2}\\|A\\|_{b} \\end{aligned}c1∥A∥a≤∥A∥b≤c2∥A∥ac1′∥A∥b≤∥A∥a≤c2∥A∥b
当AAA的矩阵范数∥A∥<1\\|{A}\\|<1∥A∥<1,则I±AI \\pm AI±A是非奇异可逆矩阵:
∥(I±A)−1∥≤11−∥A∥\\left\\|(I \\pm A)^{-1}\\right\\| \\leq \\frac{1}{1-\\|A\\|}(I±A)−1≤1−∥A∥1
前置知识2:舒尔补
A=[BCDE],det(B)≠0A=[I0DB−1I][B00E−DB−1C][IB−1C0I]\\begin{aligned} A & =\\begin{bmatrix} B & C \\\\ D & E \\end{bmatrix}, \\operatorname{det}(B) \\neq 0 \\\\ A & =\\begin{bmatrix} I & 0 \\\\ D B^{-1} & I \\end{bmatrix}\\begin{bmatrix} B & 0 \\\\ 0 & E-D B^{-1} C \\end{bmatrix}\\begin{bmatrix} I & B^{-1} C \\\\ 0 & I \\end{bmatrix} \\end{aligned}AA=[BDCE],det(B)=0=[IDB−10I][B00E−DB−1C][I0B−1CI]
前置知识3:可约矩阵
定义:
如果通过行列变换可以变成这种形式:
PAQ=[F0GH]或[FG0H]\\mathrm{PAQ}=\\left[\\begin{array}{c:c} \\boldsymbol{F} & \\boldsymbol{0} \\\\ \\hdashline \\boldsymbol{G} & \\boldsymbol{H} \\end{array}\\right]或\\left[\\begin{array}{c:c} \\boldsymbol{F} & \\boldsymbol{G} \\\\ \\hdashline \\boldsymbol{0} & \\boldsymbol{H} \\end{array}\\right]PAQ=[FG0H]或[F0GH]
左下角或右上角的0\\boldsymbol{0}0是零矩阵,则AAA是可约矩阵。
可约矩阵:
[2010867542314030]⇒[1234567800120034]\\left[\\begin{array}{llll}2 & 0 & 1 & 0 \\\\ 8 & 6 & 7 & 5 \\\\ 4 & 2 & 3 & 1 \\\\ 4 & 0 & 3 & 0\\end{array}\\right] \\Rightarrow \\left[\\begin{array}{cc:cc} 1 & 2 & 3 & 4 \\\\ 5 & 6 & 7 & 8 \\\\ \\hdashline 0 & 0 & 1 & 2 \\\\ 0 & 0 & 3 & 4 \\end{array}\\right] 2844062017330510⇒1500260037134824
不可约矩阵:
C1=[2−1−12−1⋱⋱⋱−12−1−12]C_{1}=\\left[\\begin{array}{rrrrr} 2 & -1 & & & \\\\ -1 & 2 & -1 & & \\\\ & \\ddots & \\ddots & \\ddots & \\\\ & & -1 & 2 & -1 \\\\ & & & -1 & 2 \\end{array}\\right]C1=2−1−12⋱−1⋱−1⋱2−1−12
注意上面这个矩阵对角占优,但不是严格对角占优。
前置知识4:谱半径
∣A−λI∣=0|A-\\lambda I|=0∣A−λI∣=0
定义:设λi\\lambda_iλi是AAA的特征值,
ρ(A)=max1⩽i⩽n∣λi∣\\rho(A)=\\max _{1 \\leqslant i \\leqslant n}\\left|\\lambda_{i}\\right|ρ(A)=1⩽i⩽nmax∣λi∣
称为矩阵A的谱半径。
定理:矩阵谱半径和矩阵范数有如下关系:
(1)若A是一般方阵,则P(A)不能作为矩阵的范数;
(2)若A是一般方阵,则谱半径不超过任意一种矩阵范数,即
ρ(A)≤∥A∥\\rho(A)≤\\|A\\|ρ(A)≤∥A∥
(3)若A为实对称矩阵,则谱半径可作矩阵的模,此时有ρ(A)=∥A∥2\\rho(A)=\\|A\\|_{2}ρ(A)=∥A∥2。
1.【线性方程组】直接求解:高斯消元法(LULULU分解)、LDVLDVLDV分解、LDLTLDL^TLDLT分解、UDUTUDU^TUDUT分解
1.1 高斯消元法(LULULU分解)
针对线性方程组:
AX=b\\mathrm{AX}=\\mathrm{b}AX=b
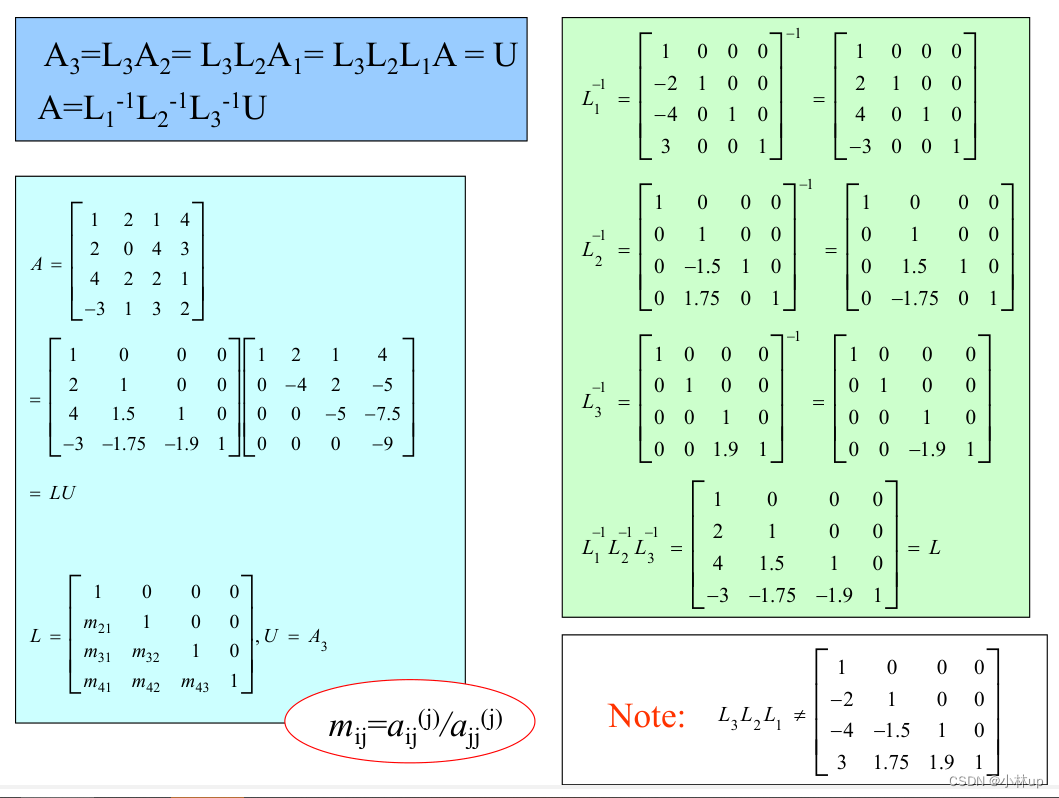
我们可以将A\\mathrm{A}A根据LU分解,分解为A=LU\\mathrm{A}=\\mathrm{LU}A=LU,其中L\\mathrm{L}L和U\\mathrm{U}U分别是下三角和上三角矩阵。
L=[∗000∗∗00∗∗∗0∗∗∗∗]U=[∗∗∗∗0∗∗∗00∗∗000∗]L=\\begin{bmatrix} \\ast & 0 & 0 & 0 \\\\ \\ast & \\ast & 0 & 0 \\\\ \\ast & \\ast & \\ast & 0 \\\\ \\ast & \\ast & \\ast & \\ast \\end{bmatrix}\\quad U=\\begin{bmatrix} \\ast & \\ast & \\ast & \\ast \\\\ 0 & \\ast & \\ast & \\ast \\\\ 0 & 0 & \\ast & \\ast \\\\ 0 & 0 & 0 & \\ast \\end{bmatrix}L=∗∗∗∗0∗∗∗00∗∗000∗U=∗000∗∗00∗∗∗0∗∗∗∗
有:
AX=b⇒(LU)X=b⇒L(UX)=b⇒LX1=bUX=X1\\begin{aligned}&\\mathrm{AX}=\\mathrm{b}\\\\ \\Rightarrow&(\\mathrm{LU}) \\mathrm{X}=\\mathrm{b} \\\\\\Rightarrow&\\mathrm{L}(\\mathrm{UX})=\\mathrm{b} \\\\ \\Rightarrow &\\mathrm{LX}_{1}=\\mathrm{b}\\quad \\mathrm{UX}=\\mathrm{X}_{1}\\end{aligned}⇒⇒⇒AX=b(LU)X=bL(UX)=bLX1=bUX=X1
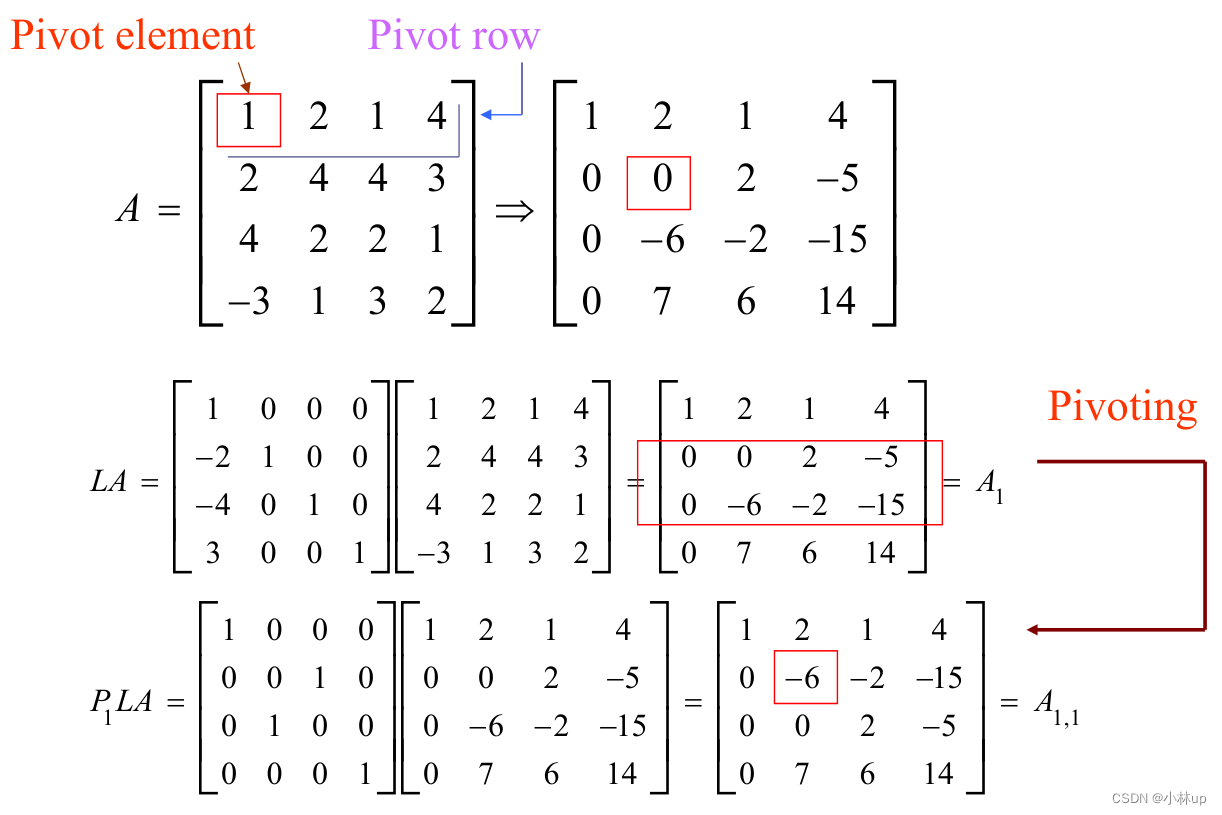
高斯消元变换三角阵:①交换行。②行乘一个因子。③某一行加到另一行上。例子:




高斯消元法中如果碰到对角线上的元素(主元素)消元为0,需要交换行,称作pivot element。
当主元素不合适由于舍入误差可能会无法求解!!

所以要选择合适的主元素:

当对角线的元素是0,可以换主元素。
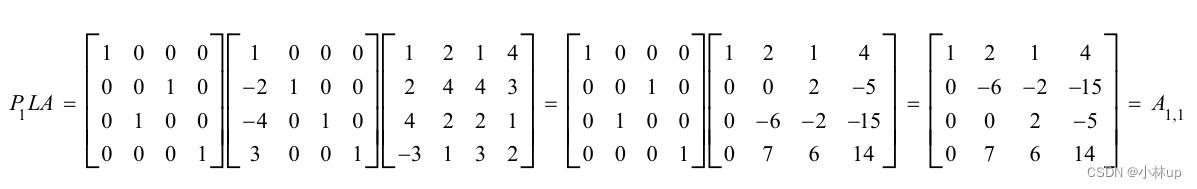
当然也可以提前换主元素。

这可以表示为:
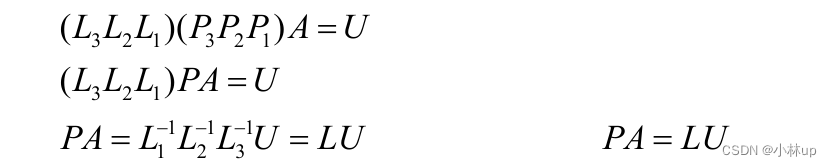
总结为:
Ax=bPA=LU⇒PAx=Pb=bˉ⇒LUx=bˉ⇒Lxˉ=bˉUx=xˉ\\begin{aligned} &A x=b \\quad P A=L U \\\\ \\Rightarrow&P A x=P b=\\bar{b} \\\\ \\Rightarrow&L U x=\\bar{b} \\\\ \\Rightarrow&L \\bar{x}=\\bar{b} \\quad U x=\\bar{x} \\end{aligned}⇒⇒⇒Ax=bPA=LUPAx=Pb=bˉLUx=bˉLxˉ=bˉUx=xˉ

计算的复杂度:
乘法和除法:∑p=1N−1(N−p)(N−p+1)=N3−N3\\sum_{p=1}^{N-1}(N-p)(N-p+1)=\\frac{N^{3}-N}{3}∑p=1N−1(N−p)(N−p+1)=3N3−N
减法:∑p=1N−1(N−p)(N−p)=2N3−3N2+N6\\sum_{p=1}^{N-1}(N-p)(N-p)=\\frac{2 N^{3}-3 N^{2}+N}{6}∑p=1N−1(N−p)(N−p)=62N3−3N2+N
这里使用了公式:∑k=1Mk=M(M+1)2,∑k=1Mk2=M(M+1)(2M+1)6\\sum_{k=1}^{M} k=\\frac{M(M+1)}{2}, \\quad \\sum_{k=1}^{M} k^{2}=\\frac{M(M+1)(2 M+1)}{6}k=1∑Mk=2M(M+1),k=1∑Mk2=6M(M+1)(2M+1)
1.2 LDVLDVLDV分解、LDLTLDL^TLDLT分解、UDUTUDU^TUDUT分解
定理:
akk(k)≠0,k=1,2,…,n⇔∣Ak∣≠0,k=1,2,…,na_{k k}^{(k)} \\neq 0, k=1,2, \\ldots, n \\Leftrightarrow\\left|A_{k}\\right| \\neq 0, k=1,2, \\ldots, nakk(k)=0,k=1,2,…,n⇔∣Ak∣=0,k=1,2,…,n其中∣Ak∣|A_{k}|∣Ak∣是方阵的kkk阶主子式。
进而我们可以知道A=LU\\mathrm{A}=\\mathrm{LU}A=LU,L\\mathrm LL是下三角矩阵,U\\mathrm UU是上三角矩阵。L\\mathrm LL的对角线元素都是1,L\\mathrm LL的行列式∣L∣|\\mathrm L|∣L∣是1,所以∣A∣=∣LU∣=∣U∣|\\mathrm{A}|=\\mathrm{|LU|}=|\\mathrm{U}|∣A∣=∣LU∣=∣U∣
让U=DR\\mathrm{U}=\\mathrm{DR}U=DR,则有:
A=LDR\\mathrm A=\\mathrm{L D R}A=LDR
其中L\\mathrm LL是下三角矩阵,D\\mathrm DD是对角矩阵,R\\mathrm RR是上三角矩阵。
当A\\mathrm AA是对称阵,A=LDLT\\mathrm{A}=\\mathrm{LDL}^{\\mathrm{T}}A=LDLT
类似的对称阵也可以表示为A=UDUT\\mathrm{A}=\\mathrm{UDU}^{\\mathrm{T}}A=UDUT
还有就是求逆矩阵的方法:
[AI]⟶Row Transformation [IA−1]\\left[\\begin{array}{ll} A & I \\end{array}\\right] \\stackrel{\\text { Row Transformation }}{\\longrightarrow}\\left[\\begin{array}{ll} I & A^{-1} \\end{array}\\right][AI]⟶ Row Transformation [IA−1]
总结:直接求解线性方程组:
1.核心算法是LU分解。 PB=LUB−1=U−1L−1P\\begin{aligned} P B & = L U \\\\ B^{-1} & = U^{-1} L^{-1} P \\end{aligned}PBB−1=LU=U−1L−1P
2.迭代求解器可能不能收敛或计算成本较高。
1.3 误差分析(从条件数的角度)
矩阵范数回顾前置知识1.
①给bbb一个小的扰动对xxx有什么影响嘛?
Ax=bA(x+δx)=b+δbAδx=δb∥δx∥=∥A−1δb∥≤∥A−1∥δb∥∥Ax∥≤∥A∥∥x∥,∥x∥≥∥Ax∥∥A∥=∥b∥∥A∥∥δx∥∥x∥≤∥A∥∥A−1∥∥δb∥∥b∥=cond(A)∥δb∥∥b∥\\begin{aligned} &A x=b \\\\ &A(x+\\delta x)=b+\\delta b \\\\ &A \\delta x=\\delta b \\\\ &\\|\\delta x\\|=\\left\\|A^{-1} \\delta b\\right\\| \\leq\\left\\|A^{-1}\\right\\| \\delta b \\| \\\\ &\\|A x\\| \\leq\\|A\\|\\|x\\|, \\quad\\|x\\| \\geq \\frac{\\|A x\\|}{\\|A\\|}=\\frac{\\|b\\|}{\\|A\\|} \\\\ &\\frac{\\|\\delta x\\|}{\\|x\\|} \\leq\\|A\\|\\left\\|A^{-1}\\right\\| \\frac{\\|\\delta b\\|}{\\|b\\|}=\\operatorname{cond}(A) \\frac{\\|\\delta b\\|}{\\|b\\|} \\end{aligned}Ax=bA(x+δx)=b+δbAδx=δb∥δx∥=A−1δb≤A−1δb∥∥Ax∥≤∥A∥∥x∥,∥x∥≥∥A∥∥Ax∥=∥A∥∥b∥∥x∥∥δx∥≤∥A∥A−1∥b∥∥δb∥=cond(A)∥b∥∥δb∥
②给AAA一个小的扰动对xxx有什么影响嘛?
Ax=b(A+δA)(x+δx)=bAδx+δA(x+δx)=0∥δx∥=∥A−1δA(x+δx)∥≤∥A−1∥δA∥∥(∥x∥+∥δx∥)∥δx∥∥x∥≤∥A−1∥∥δA∥(1+∥δx∥∥x∥)∥δx∥∥x∥≤∥A−1∥∥δA∥1−∥A−1∥∥δA∥=∥A−1∥∥A∥∥δA∥∥A∥1−∥A−1∥∥A∥∥δA∥∥A∥=cond(A)∣∥δA∥∥A∥1−cond(A)∣∥δA∥∥A∥\\begin{aligned} &A x = b \\\\ &(A+\\delta A)(x+\\delta x) = b \\\\ &A \\delta x+\\delta A(x+\\delta x) = 0 \\\\ &\\|\\delta x\\| = \\left\\|A^{-1} \\delta A(x+\\delta x)\\right\\| \\leq\\left\\|A^{-1}\\right\\| \\delta A\\|\\|(\\|x\\|+\\|\\delta x\\|) \\\\ &\\frac{\\|\\delta x\\|}{\\|x\\|} \\leq\\left\\|A^{-1}\\right\\|\\|\\delta A\\|\\left(1+\\frac{\\|\\delta x\\|}{\\|x\\|}\\right) \\\\ &\\frac{\\|\\delta x\\|}{\\|x\\|} \\leq \\frac{\\left\\|A^{-1}\\right\\|\\|\\delta A\\|}{1-\\left\\|A^{-1}\\right\\|\\|\\delta A\\|}=\\frac{\\|A^{-1}\\|\\|A\\|\\frac{\\|\\delta A\\|} {\\|A\\|}}{1-\\|A^{-1}\\|\\|A\\|\\frac{\\|\\delta A\\|} {\\|A\\|}}=\\frac{cond(A)|\\frac{\\|\\delta A\\|} {\\|A\\|}}{1-cond(A)|\\frac{\\|\\delta A\\|} {\\|A\\|}} \\end{aligned}Ax=b(A+δA)(x+δx)=bAδx+δA(x+δx)=0∥δx∥=A−1δA(x+δx)≤A−1δA∥∥(∥x∥+∥δx∥)∥x∥∥δx∥≤A−1∥δA∥(1+∥x∥∥δx∥)∥x∥∥δx∥≤1−∥A−1∥∥δA∥A−1∥δA∥=1−∥A−1∥∥A∥∥A∥∥δA∥∥A−1∥∥A∥∥A∥∥δA∥=1−cond(A)∣∥A∥∥δA∥cond(A)∣∥A∥∥δA∥
这里需要假设1−cond(A)∥δA∥∥A∥≥01-cond(A)\\frac{\\|\\delta A\\|} {\\|A\\|}\\ge01−cond(A)∥A∥∥δA∥≥0或δA\\delta{A}δA足够小。其中cond(A)=∥A−1∥∥A∥cond(A)=\\left\\|A^{-1}\\right\\|\\|A\\|cond(A)=A−1∥A∥称为条件数。
当条件数很大时矩阵是病态的。例如:
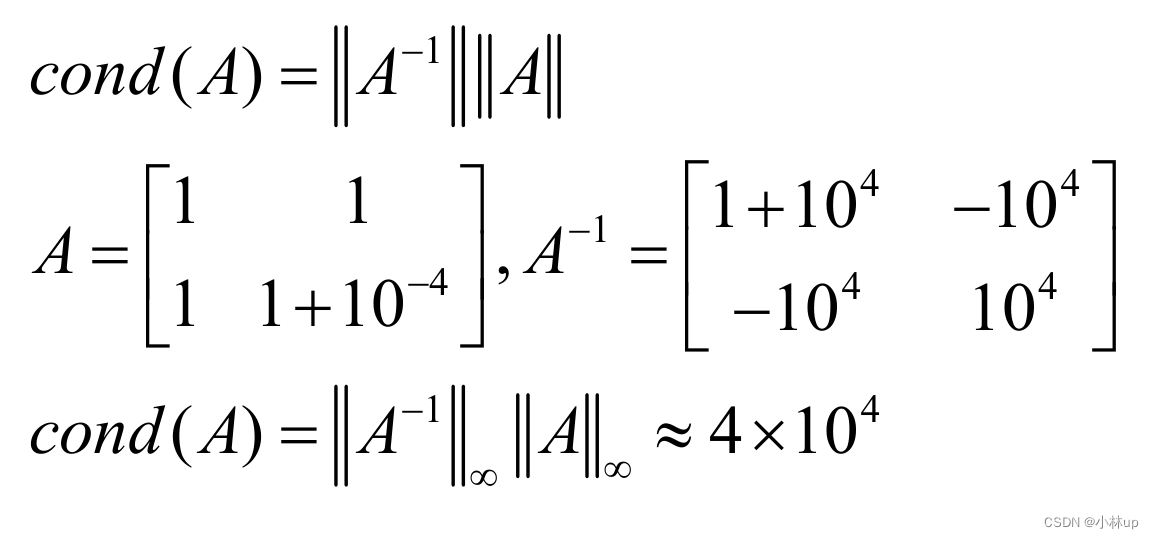

其他判断条件数的方法
- 当两行中的对应元素的比率非常接近时,cond(A)可能很大。
- 元素之间的差异很大,cond(A)也可能很大。
- 对A或b做一个小的扰动,然后解方程。如果解差很大,矩阵就没有条件。
于是我们就想把病态的矩阵转为非病态的矩阵:左乘一个矩阵,改变稳定性。
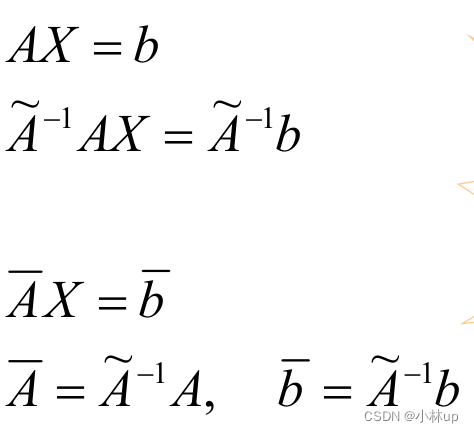
找到合适的A~−1\\widetilde{A}^{-1}A−1是关键
2. 【线性方程组】间接迭代求解:Jacobi方法, Gauss-Seidel方法
我们能不能使用类似不动点迭代的思想进行求解呢?我们要考虑:
- 怎么选择迭代形式
- 迭代要收敛
- 收敛的速度也要保证

2.1 Jacobi方法
A=L+D+Ux=D−1(b−Lx−Ux)x(k+1)=D−1(b−Lx(k)−Ux(k))\\begin{aligned} {A} & = {L}+{D}+{U} \\\\ {x} & = {D}^{-1}({~b}-{Lx}-{Ux}) \\\\ {x}^{({k}+1)} & = {D}^{-1}\\left({~b}-{Lx}{ }^{({k})}-{Ux}^{({k})}\\right) \\end{aligned}Axx(k+1)=L+D+U=D−1( b−Lx−Ux)=D−1( b−Lx(k)−Ux(k))
x(k+1)=Bx(k)+c,B=−D−1(L+U),c=D−1bx^{({k}+1)}={B} x^{({k})}+{c}, \\quad {B}=-{D}^{-1}({~L}+{U}), \\quad {c}={D}^{-1} {b}x(k+1)=Bx(k)+c,B=−D−1( L+U),c=D−1b
例子
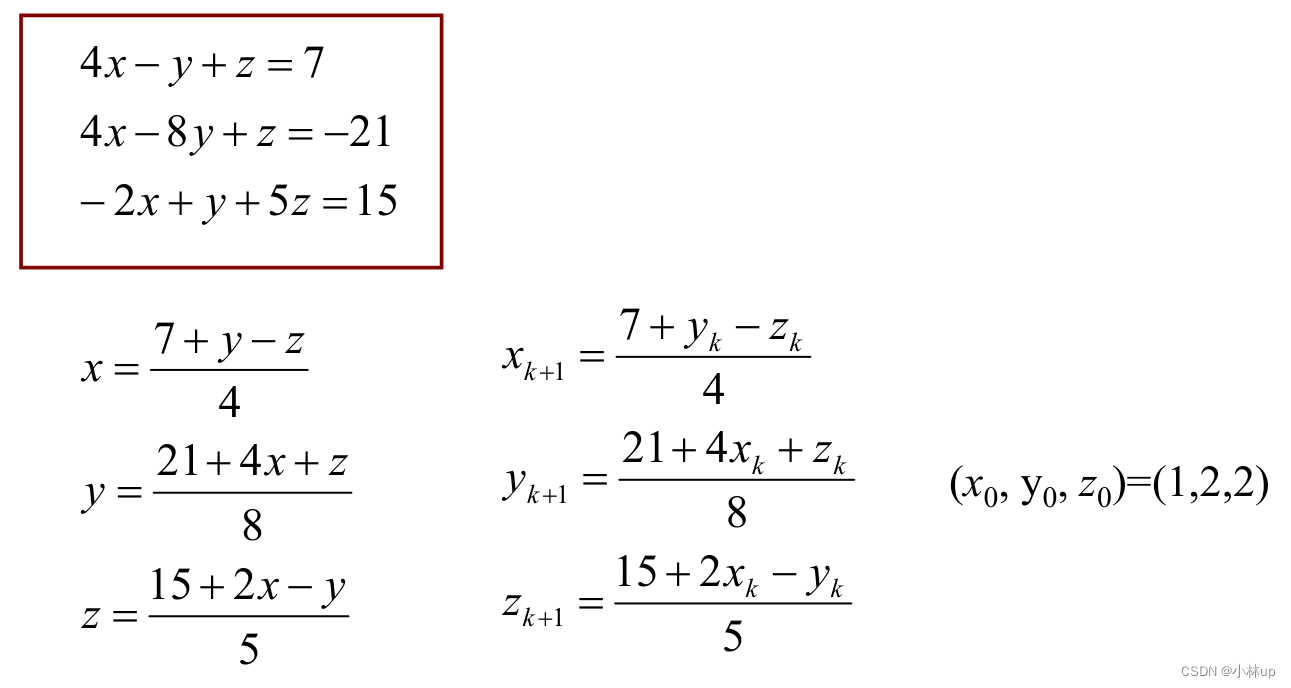
具体编程的实现可以有:
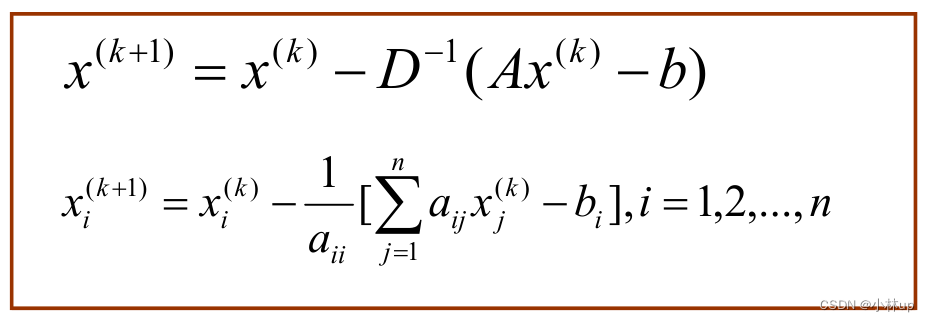
或者

然而同一个方程组不同的方程顺序可能会不收敛。

所以什么时候会收敛呢?
定义:
矩阵AAA严格对角占优:∣akk∣>∑j=1,j≠kN∣akj∣k=1,2,…,N\\left|a_{k k}\\right|>\\sum_{j=1, j \\neq k}^{N}\\left|a_{k j}\\right| \\quad k=1,2, \\ldots, N∣akk∣>j=1,j=k∑N∣akj∣k=1,2,…,N
矩阵AAA表示为:
A=[a11a12⋯a1Na21a22⋯a2N⋮⋮⋮aN1aN2⋯aNN]A=\\begin{bmatrix} a_{11} & a_{12} & \\cdots & a_{1 N} \\\\ a_{21} & a_{22} & \\cdots & a_{2 N} \\\\ \\vdots & \\vdots & & \\vdots \\\\ & & & \\\\ a_{N 1} & a_{N 2} & \\cdots & a_{N N} \\end{bmatrix}A=a11a21⋮aN1a12a22⋮aN2⋯⋯⋯a1Na2N⋮aNN
例子:
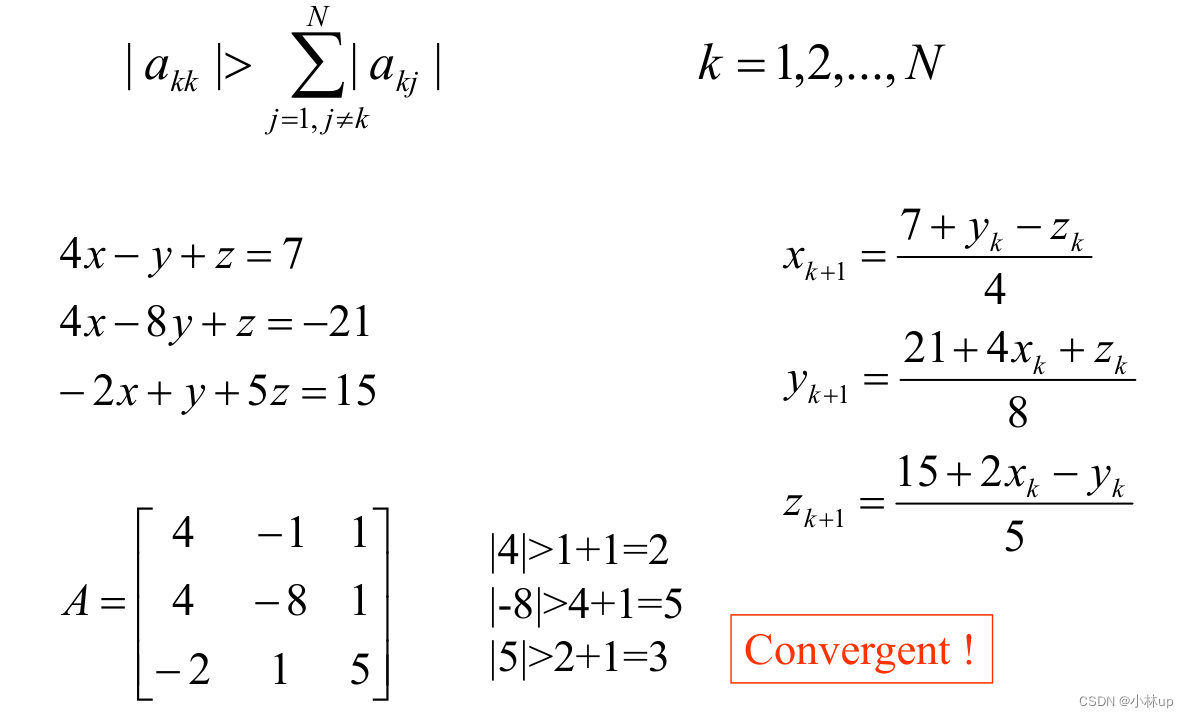

严格对角占优只能算是Jacobi方法的一个充分条件。
2.2 Gauss-Seidel方法
A=L+D+Ux=D−1(b−Lx−Ux)x(k+1)=D−1(b−Lx(k+1)−Ux(k))\\begin{aligned} &{A} = {L}+{D}+{U} \\\\ &{x} = {D}^{-{1}}({b}-{L} {x}-{U} {x})\\\\ &{x}^{({k}+1)}={D}^{-1}\\left({b}-{L} {x}^{({k}+1)}-{U} {x}^{({k})}\\right) \\end{aligned}A=L+D+Ux=D−1(b−Lx−Ux)x(k+1)=D−1(b−Lx(k+1)−Ux(k))
A=L+D+U(L+D)x(k+1)+Ux(k)=bx(k+1)=−(L+D)−1Ux(k)+(L+D)−1b\\begin{aligned} &{A} = {L}+{D}+{U} \\\\ &({L}+{D}) {x}^{({k}+1)}+{U} {x}^{({k})} = {b} \\\\ &{x}^{({k}+1)}=-({L}+{D})^{-1} {U} {x}^{({k})}+({L}+{D})^{-1} {b}\\\\ \\end{aligned}A=L+D+U(L+D)x(k+1)+Ux(k)=bx(k+1)=−(L+D)−1Ux(k)+(L+D)−1b
x(k+1)=Bx(k)+c,B=−(L+D)−1U,c=(L+D)−1bx^{({k}+1)}={B} x^{({k})}+{c}, \\quad {B}=-({L}+{D})^{-1} {U} , \\quad {c}=({L}+{D})^{-1} {b}x(k+1)=Bx(k)+c,B=−(L+D)−1U,c=(L+D)−1b

迭代速度比Jacobi方法更快!
2.3 Jacobi方法, Gauss-Seidel方法收敛的条件
充分条件1
矩阵AAA满足下面任一①严格对角占优 ②不可约矩阵(回顾前置知识3),使用Jacobi方法, Gauss-Seidel方法都收敛。
充分必要条件
矩阵的谱半径小于1。
ρ(B)=maxi∣λi∣<1∣B−λiI∣=0\\rho(B)=\\max _{i}\\left|\\lambda_{i}\\right|<1\\quad \\left|B-\\lambda_{i} I\\right|=0ρ(B)=imax∣λi∣<1∣B−λiI∣=0
以下是对实对称阵说明
x=Bx+gx(k+1)=Bx(k)+ge(k+1)=Be(k)=Bk+1e(0)【e(k+1)=x(k+1)−x(k)】e(0)=c1V1+c2V2+…+cnVn,BVi=λiVie(k+1)=c1λ1k+1V1+c2λ2k+1V2+…+cnλnk+1Vn→0when ∣λi∣<1\\begin{aligned} &x = B x+g \\\\ &x^{(k+1)} = B x^{(k)}+g \\\\ &e^{(k+1)} = B e^{(k)} = B^{k+1} e^{(0)} 【e^{(k+1)} =x^{(k+1)} -x^{(k)}】\\\\ & e^{(0)} = c_{1} V_{1}+c_{2} V_{2}+\\ldots+c_{n} V_{n}, \\quad B V_{i} = \\lambda_{i} V_{i} \\\\ &e^{(k+1)} = c_{1} \\lambda_{1}^{k+1} V_{1}+c_{2} \\lambda_{2}^{k+1} V_{2}+\\ldots+c_{n} \\lambda_{n}^{k+1} V_{n} \\rightarrow 0 \\quad \\text { when }\\left|\\lambda_{i}\\right|<1 \\end{aligned}x=Bx+gx(k+1)=Bx(k)+ge(k+1)=Be(k)=Bk+1e(0)【e(k+1)=x(k+1)−x(k)】e(0)=c1V1+c2V2+…+cnVn,BVi=λiVie(k+1)=c1λ1k+1V1+c2λ2k+1V2+…+cnλnk+1Vn→0 when ∣λi∣<1
对一般的矩阵形式可以用Jordan形式证明
B=TJT−1Bk=TJkT−1Jk=diag(Jr1k(λ1),Jr2k(λ2),…,Jrpk(λp))→0,when ∣λi∣<1Jri(λi)=[λi1λi1⋱1λi]\\begin{aligned} &B = T J T^{-1} \\\\ &B^{k} = T J^{k} T^{-1} \\\\ &J^{k} = \\operatorname{diag}\\left(J_{r_{1}}^{k}\\left(\\lambda_{1}\\right), J_{r_{2}}^{k}\\left(\\lambda_{2}\\right), \\ldots, J_{r_{p}}^{k}\\left(\\lambda_{p}\\right)\\right) \\rightarrow 0, \\text { when }\\left|\\lambda_{i}\\right|<1 \\\\ &J_{r_{i}}\\left(\\lambda_{i}\\right) = \\begin{bmatrix} \\lambda_{i} & 1 & & \\\\ & \\lambda_{i} & 1 & \\\\ & & \\ddots & 1 \\\\ & & \\lambda_{i} \\end{bmatrix} \\end{aligned}B=TJT−1Bk=TJkT−1Jk=diag(Jr1k(λ1),Jr2k(λ2),…,Jrpk(λp))→0, when ∣λi∣<1Jri(λi)=λi1λi1⋱λi1
定理:对于矩阵的任意范数,谱半径都小于矩阵的范数。
ρ(B)≤∥B∥\\rho(B) \\leq\\|B\\|ρ(B)≤∥B∥
于是有
充分条件2
满足条件∥B∥<1\\|B\\|<1∥B∥<1,矩阵AAA使用Jacobi方法, Gauss-Seidel方法都收敛。
说明:以下等价
Bk→0⇔∥Bk∥→0⇔ρ(B)<1B^{k} \\rightarrow 0 \\Leftrightarrow\\left\\|B^{k}\\right\\| \\rightarrow 0 \\Leftrightarrow \\rho(B)<1\\\\ Bk→0⇔Bk→0⇔ρ(B)<1
∥Bk∥≤∥B∥∥Bk−1∥≤∥B∥k\\left\\|B^{k}\\right\\| \\leq\\|B\\|\\left\\|B^{k-1}\\right\\| \\leq\\|B\\|^{k}Bk≤∥B∥Bk−1≤∥B∥k
充分条件3
定理:矩阵AAA满足下面任一条件:①严格对角占优 ②不可约矩阵(回顾前置知识3),并且对角线上元素大于0,AAA是个正定矩阵!
如果矩阵AAA是对称正定矩阵,使用Jacobi方法, Gauss-Seidel方法都收敛。
一张关系图说明收敛的条件
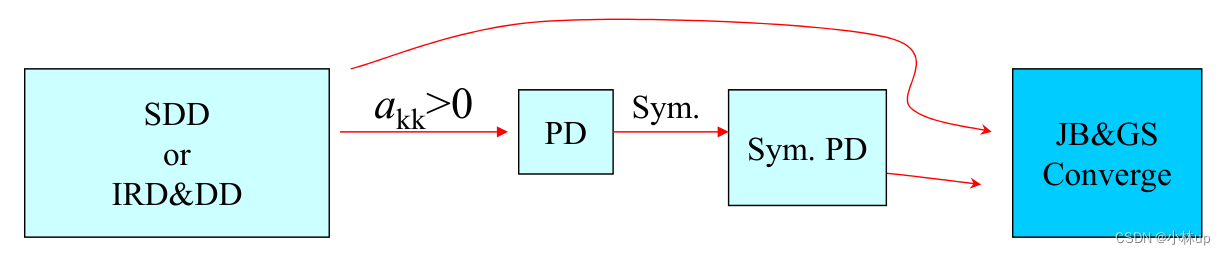
2.4 预测迭代次数
定理:设基本迭代的迭代矩阵∥B∥=q<1\\|B\\|=q<1∥B∥=q<1,若∥x(k+1)−x(k)∥⩽ε\\left\\|x^{(k+1)}-x^{(k)}\\right\\| \\leqslant \\varepsilonx(k+1)−x(k)⩽ε,则∥x(k)−x∥⩽ε1−q\\left\\|x^{(k)}-x\\right\\| \\leqslant \\frac{\\varepsilon}{1-q}x(k)−x⩽1−qε
容易证明:∥Xk−X∗∥≤11−∥B∥∥Xk+1−Xk∥∥Xk−X∗∥≤∥B∥k1−∥B∥∥X1−X0∥\\begin{aligned} \\left\\|X_{k}-X^{*}\\right\\| \\leq\\frac{1}{1-\\|B\\|}\\left\\|X_{k+1}-X_{k}\\right\\| \\\\ \\left\\|X_{k}-X^{*}\\right\\| \\leq \\frac{\\|B\\|^{k}}{1-\\|B\\|}\\left\\|X_{1}-X_{0}\\right\\| \\end{aligned}∥Xk−X∗∥≤1−∥B∥1∥Xk+1−Xk∥∥Xk−X∗∥≤1−∥B∥∥B∥k∥X1−X0∥
这个定理使用的两种方式:
1.预测需要的迭代次数
2.使用∣xk+1−xk∣|x_{k+1}-x_k|∣xk+1−xk∣看是否停止迭代。
预测迭代次数类似不动点迭代收敛的推导: 就不具体展开了。
2.5 连续超松弛方法(The Method of Successive Over-Relaxation【SOR】)
(L+D)x~(k+1)+Ux(k)=bx(k+1)=ωx~(k+1)+(1−ω)x(k)xi(k+1)=(1−ω)xi(k)+ωaii(bi−∑j=1i−1aijxj(k+1)−∑j=i+1naijxj(k))=(1−ω)xi(k)+ωaii(bi−∑j=1i−1aijxj(k+1)−aiixi(k)−∑j=i+1naijxj(k)+aiixi(k))=xi(k)+ωaii(bi−∑j=1i−1aijxj(k+1)−∑j=inaijxj(k))⇒x(k+1)=x(k)+ωD−1(b−Lx(k+1)−Dx(k)−Ux(k))⇒Dx(k+1)=Dx(k)+ω(b−Lx(k+1)−Dx(k)−Ux(k))⇒(D+ωL)x(k+1)=[(1−ω)D−ωU]x(k)+ωb⇒x(k+1)=(D+ωL)−1[(1−ω)D−ωU]x(k)+ω(D+ωL)−1b\\begin{aligned} &(L+D) \\tilde{x}^{(k+1)}+U x^{(k)} = b \\\\ &x^{(k+1)} = \\omega \\tilde{x}^{(k+1)}+(1-\\omega) x^{(k)} \\\\ &x_{i}^{(k+1)} = (1-\\omega) x_{i}^{(k)}+\\frac{\\omega}{a_{i i}}\\left(b_{i}-\\sum_{j = 1}^{i-1} a_{i j} x_{j}^{(k+1)}-\\sum_{j = i+1}^{n} a_{i j} x_{j}^{(k)} \\right)\\\\ &= (1-\\omega) x_{i}^{(k)}+\\frac{\\omega}{a_{i i}}\\left(b_{i}-\\sum_{j = 1}^{i-1} a_{i j} x_{j}^{(k+1)}-a_{i i} x_{i}^{(k)}-\\sum_{j = i+1}^{n} a_{i j} x_{j}^{(k)}+a_{i i} x_{i}^{(k)}\\right) \\\\ & = x_{i}^{(k)}+\\frac{\\omega}{a_{i i}}\\left(b_{i}-\\sum_{j = 1}^{i-1} a_{i j} x_{j}^{(k+1)}-\\sum_{j = i}^{n} a_{i j} x_{j}^{(k)}\\right)\\\\ \\Rightarrow &x^{(k+1)} = x^{(k)}+\\omega D^{-1}\\left(b-L x^{(k+1)}-D x^{(k)}-U x^{(k)}\\right) \\\\ \\Rightarrow&D x^{(k+1)} = D x^{(k)}+\\omega\\left(b-L x^{(k+1)}-D x^{(k)}-U x^{(k)}\\right) \\\\ \\Rightarrow&(D+\\omega L) x^{(k+1)} = [(1-\\omega) D-\\omega U] x^{(k)}+\\omega b \\\\ \\Rightarrow&x^{(k+1)} = (D+\\omega L)^{-1}[(1-\\omega) D-\\omega U] x^{(k)}+\\omega(D+\\omega L)^{-1} b \\end{aligned}⇒⇒⇒⇒(L+D)x~(k+1)+Ux(k)=bx(k+1)=ωx~(k+1)+(1−ω)x(k)xi(k+1)=(1−ω)xi(k)+aiiω(bi−j=1∑i−1aijxj(k+1)−j=i+1∑naijxj(k))=(1−ω)xi(k)+aiiω(bi−j=1∑i−1aijxj(k+1)−aiixi(k)−j=i+1∑naijxj(k)+aiixi(k))=xi(k)+aiiω(bi−j=1∑i−1aijxj(k+1)−j=i∑naijxj(k))x(k+1)=x(k)+ωD−1(b−Lx(k+1)−Dx(k)−Ux(k))Dx(k+1)=Dx(k)+ω(b−Lx(k+1)−Dx(k)−Ux(k))(D+ωL)x(k+1)=[(1−ω)D−ωU]x(k)+ωbx(k+1)=(D+ωL)−1[(1−ω)D−ωU]x(k)+ω(D+ωL)−1b
x(k+1)=Bx(k)+c,B=(D+ωL)−1[(1−ω)D−ωU],c=ω(D+ωL)−1bx^{({k}+1)}={B} x^{({k})}+{c}, \\quad {B}= (D+\\omega L)^{-1}[(1-\\omega) D-\\omega U] , \\quad {c}=\\omega(D+\\omega L)^{-1} bx(k+1)=Bx(k)+c,B=(D+ωL)−1[(1−ω)D−ωU],c=ω(D+ωL)−1b
还有另一种形式:
(L+D)x~(k+1)+Ux(k)=bx(k+1)=ωx~(k+1)+(1−ω)x(k)⇒x(k+1)=ω(−(L+D)−1Ux(k)+(L+D)−1b)+(1−ω)x(k)⇒x(k+1)=[(1−ω)I−ω(L+D)−1U]x(k)+ω(L+D)−1b\\begin{aligned} &(L+D) \\tilde{x}^{(k+1)}+U x^{(k)} = b \\\\ &x^{(k+1)} = \\omega \\tilde{x}^{(k+1)}+(1-\\omega) x^{(k)} \\\\ \\Rightarrow&x^{(k+1)} = \\omega \\left( -({L}+{D})^{-1} {U} {x}^{({k})}+({L}+{D})^{-1} {b}\\right)+(1-\\omega) x^{(k)}\\\\ \\Rightarrow&x^{(k+1)}=\\left[(1-\\omega) I-\\omega(L+D)^{-1} U\\right] x^{(k)}+\\omega(L+D)^{-1} b \\end{aligned}⇒⇒(L+D)x~(k+1)+Ux(k)=bx(k+1)=ωx~(k+1)+(1−ω)x(k)x(k+1)=ω(−(L+D)−1Ux(k)+(L+D)−1b)+(1−ω)x(k)x(k+1)=[(1−ω)I−ω(L+D)−1U]x(k)+ω(L+D)−1b
x(k+1)=Bx(k)+c,B=[(1−ω)I−ω(L+D)−1U],c=ω(L+D)−1bx^{({k}+1)}={B} x^{({k})}+{c}, \\quad {B}=\\left[(1-\\omega) I-\\omega(L+D)^{-1} U\\right] , \\quad {c}=\\omega(L+D)^{-1} bx(k+1)=Bx(k)+c,B=[(1−ω)I−ω(L+D)−1U],c=ω(L+D)−1b
可以根据ω可以根据\\omega可以根据ω取值不同分类如下:
0<ω<2ω=1:Gauss - Seidel 0<ω<1:Under - Relaxation 1<ω<2:SOR \\begin{align} &0<\\omega<2 \\\\ &\\omega = 1: \\text { Gauss - Seidel } \\\\ &0<\\omega<1: \\text { Under - Relaxation } \\\\ &1<\\omega<2: \\text { SOR } \\end{align}0<ω<2ω=1: Gauss - Seidel 0<ω<1: Under - Relaxation 1<ω<2: SOR
SOR 收敛的条件和Jacobi方法, Gauss-Seidel方法相同:
1.当系数矩阵A为强对角占优矩阵时,SOR方法收敛;
2.当系数矩阵A为不可约对角占优矩阵时,SOR方法收敛;
3.当系数矩阵A为对称正定矩阵时,SOR方法收敛。
x(k+1)=Bx(k)+cx^{({k}+1)}={B} x^{({k})}+{c}x(k+1)=Bx(k)+c
BBB是关于松弛因子ω\\omegaω的一个函数,所以ω\\omegaω应该取多少呢?
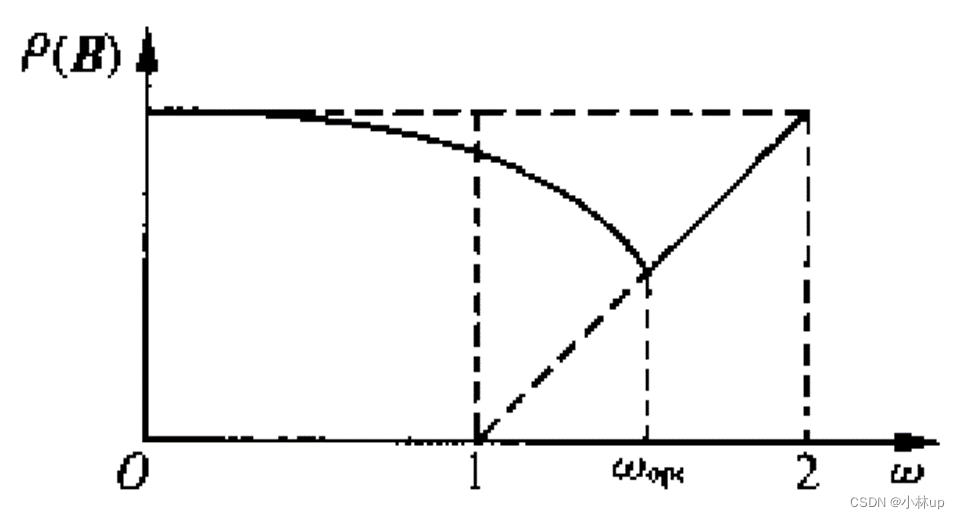
可惜的是,ωopt\\omega_{opt}ωopt无法准确求得,只能估算,下面给出两种估算方法。
方法1: 先用ω=1\\omega=1ω=1算得x(1)x^{(1)}x(1)和x(2)x^{(2)}x(2),再用ω=1.1\\omega=1.1ω=1.1算得x~(1)\\tilde x^{(1)}x~(1)和x~(2)\\tilde x^{(2)}x~(2);比较∥x(1)−x(2)∥\\|x^{(1)}-x^{(2)}\\|∥x(1)−x(2)∥和∥x~(1)−x~(2)∥\\|\\tilde x^{(1)}-\\tilde x^{(2)}\\|∥x~(1)−x~(2)∥的大小,量值∥x~(1)−x~(2)∥\\|\\tilde x^{(1)}-\\tilde x^{(2)}\\|∥x~(1)−x~(2)∥较大说明取ω=1.1\\omega=1.1ω=1.1时迭代收敛快:继续选ω=1.2\\omega=1.2ω=1.2计算且与ω=1.1\\omega=1.1ω=1.1的情形比较,不断改进ω\\omegaω的值直到接近ω\\omegaω为止、
方法2: 用ω=1.9\\omega=1.9ω=1.9和ω=1.8\\omega=1.8ω=1.8计算,判断比较相应松弛迭代收敛的快慢表现;不断改进参数w的取值,在ωopt\\omega_{opt }ωopt附近还可作些适当的微调处理。
例子:
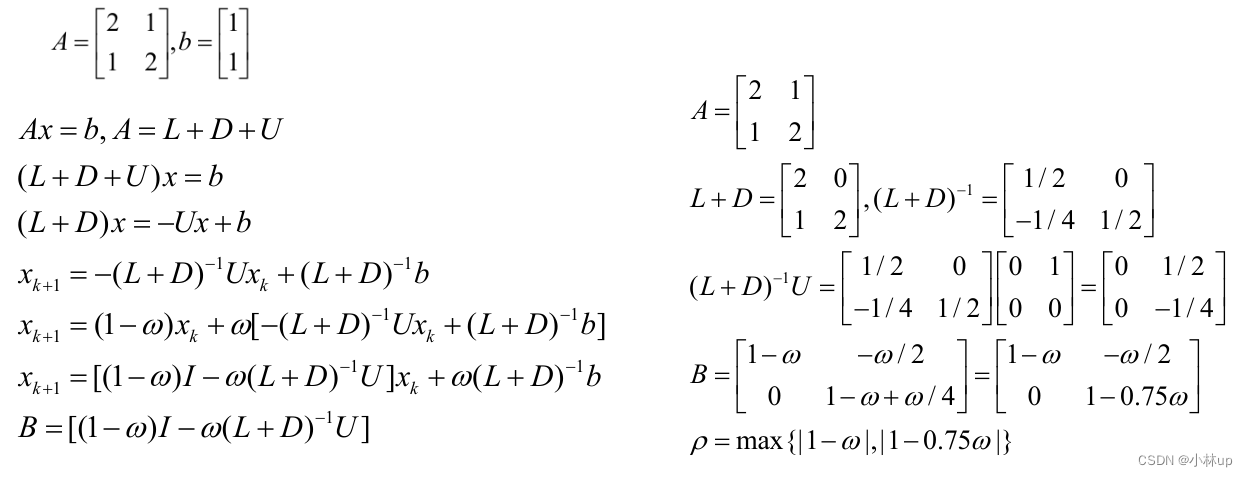
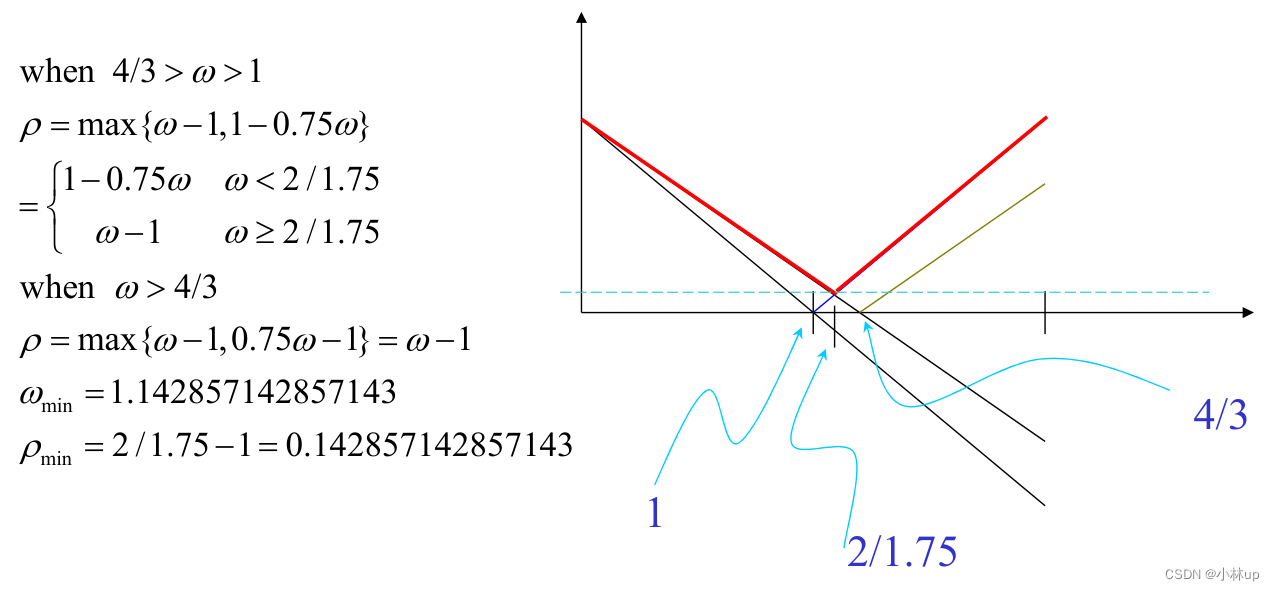
在SOR方法计算下,当系数矩阵BBB的谱半径小于1但是非常接近1的时候,收敛速度较慢。
来看下面这个例子:
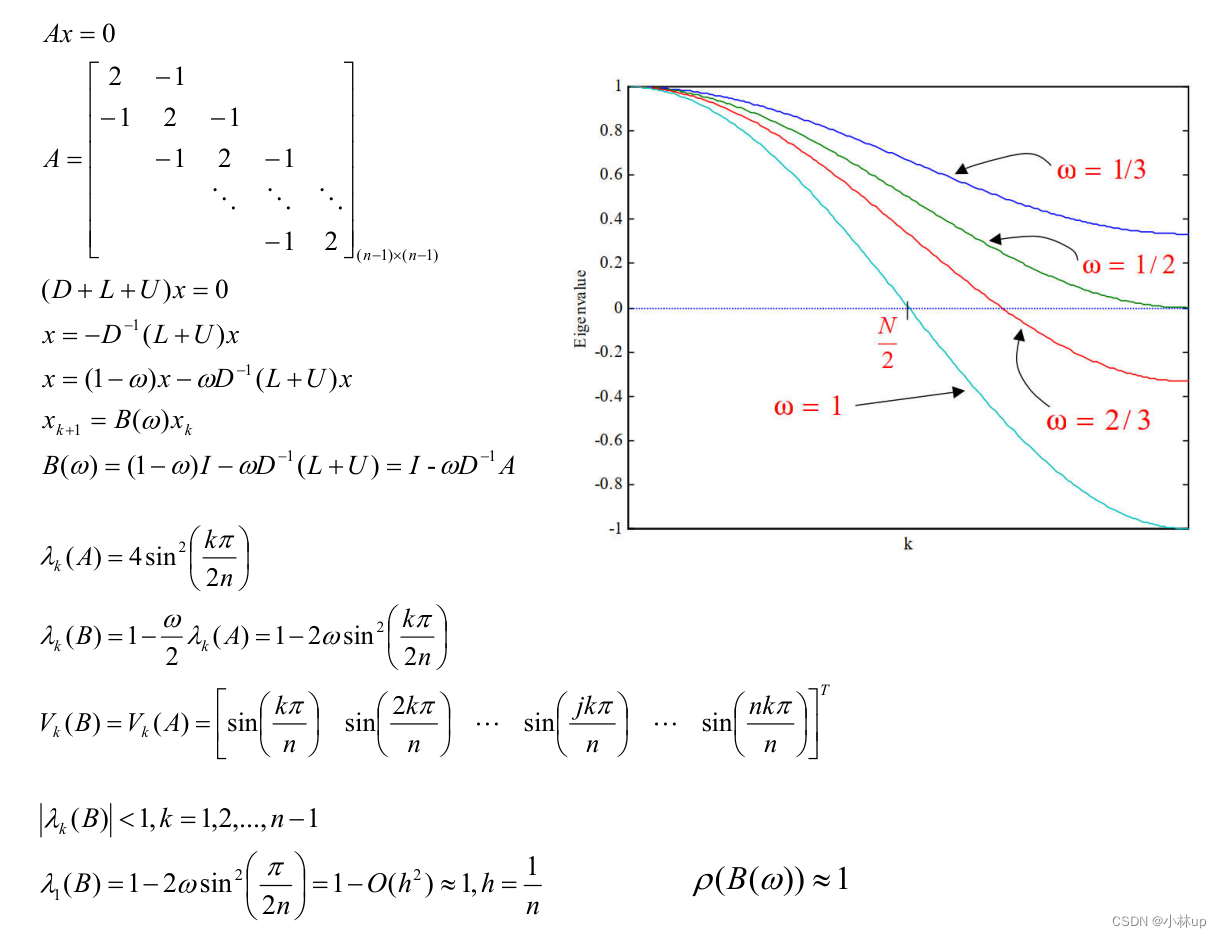

2.6 总结:Jacobi方法, Gauss-Seidel方法对比:

2.7 对称矩阵的Gauss-Seidel方法
对于一个对称矩阵AAA
A=L+D+LTA=L+D+L^TA=L+D+LT
DDD是AAA的对角线组成的对角阵,LLL是AAA的下三角矩阵,由于对称,LTL^TLT是AAA的上三角矩阵。
令M=(L+D)D−1(L+D)TM = (L+D) D^{-1}(L+D)^{T}M=(L+D)D−1(L+D)T
x(k+1)=x(k)+M−1(b−Ax(k))=M−1b+M−1(M−A)x(k)=M−1b+M−1(M−L−D−LT)x(k)=M−1b+M−1((L+D)D−1(L+D)T−L−D−LT)x(k)=M−1b+M−1(LD−1LT+LD−1DT+DD−1LT+DD−1DT−L−D−LT)x(k)=M−1b+M−1(LD−1LT+L+LT+DT−L−D−LT)x(k)=M−1b+M−1LD−1LTx(k)=M−1b+Bx(k)\\begin{aligned}x^{(k+1)}&=x^{(k)}+M^{-1}\\left(b-A x^{(k)}\\right)\\\\ &=M^{-1} b+M^{-1} (M-A)x^{(k)}\\\\ &=M^{-1} b+M^{-1} (M-L-D-L^{T})x^{(k)}\\\\ &=M^{-1} b+M^{-1} ( (L+D) D^{-1}(L+D)^{T}-L-D-L^{T})x^{(k)}\\\\ &=M^{-1} b+M^{-1} (L D^{-1} L^{T}+L D^{-1} D^{T}+D D^{-1} L^{T}+D D^{-1} D^{T}-L-D-L^{T} )x^{(k)}\\\\ &=M^{-1} b+M^{-1} (L D^{-1} L^{T}+L+L^{T}+D^T-L-D-L^{T} )x^{(k)}\\\\ &=M^{-1} b+M^{-1} L D^{-1} L^{T} x^{(k)}\\\\ &=M^{-1} b+B x^{(k)}\\end{aligned}x(k+1)=x(k)+M−1(b−Ax(k))=M−1b+M−1(M−A)x(k)=M−1b+M−1(M−L−D−LT)x(k)=M−1b+M−1((L+D)D−1(L+D)T−L−D−LT)x(k)=M−1b+M−1(LD−1LT+LD−1DT+DD−1LT+DD−1DT−L−D−LT)x(k)=M−1b+M−1(LD−1LT+L+LT+DT−L−D−LT)x(k)=M−1b+M−1LD−1LTx(k)=M−1b+Bx(k)
式中的BBB:
B=M−1LD−1LT\\begin{aligned} B & = M^{-1} L D^{-1} L^{T} \\end{aligned}B=M−1LD−1LT
2.8 Krylov方法(Krylov methods)
Ax=bq(λ)=∣A−λI∣=a0+a1λ+…+anλn=0q(A)=a0I+a1A+…+anAn=0−1a0A(a1I+…+anAn−1)=IA−1=−1a0(a1I+…+anAn−1)x=A−1b=−1a0(a1b+…+anAn−1b)∈span(b,Ab,A2b,…,An−1b)x∗=∑iciAib\\begin{aligned} &A x = b \\\\ &q(\\lambda) = |A-\\lambda I| = a_{0}+a_{1} \\lambda+\\ldots+a_{n} \\lambda^{n} & = 0 \\\\ &q(A) = a_{0} I+a_{1} A+\\ldots+a_{n} A^{n} = 0 \\\\ &-\\frac{1}{a_{0}} A\\left(a_{1} I+\\ldots+a_{n} A^{n-1}\\right) = I \\\\ &A^{-1} = -\\frac{1}{a_{0}}\\left(a_{1} I+\\ldots+a_{n} A^{n-1}\\right) \\\\ &x = A^{-1} b = -\\frac{1}{a_{0}}\\left(a_{1} b+\\ldots+a_{n} A^{n-1} b\\right) \\in \\operatorname{span}\\left(b, A b, A^{2} b, \\ldots, A^{n-1} b\\right) \\\\ &x^{*} = \\sum_{i} c_{i} A^{i} b \\end{aligned}Ax=bq(λ)=∣A−λI∣=a0+a1λ+…+anλnq(A)=a0I+a1A+…+anAn=0−a01A(a1I+…+anAn−1)=IA−1=−a01(a1I+…+anAn−1)x=A−1b=−a01(a1b+…+anAn−1b)∈span(b,Ab,A2b,…,An−1b)x∗=i∑ciAib=0
x∗x^*x∗的维数可小于nnn!
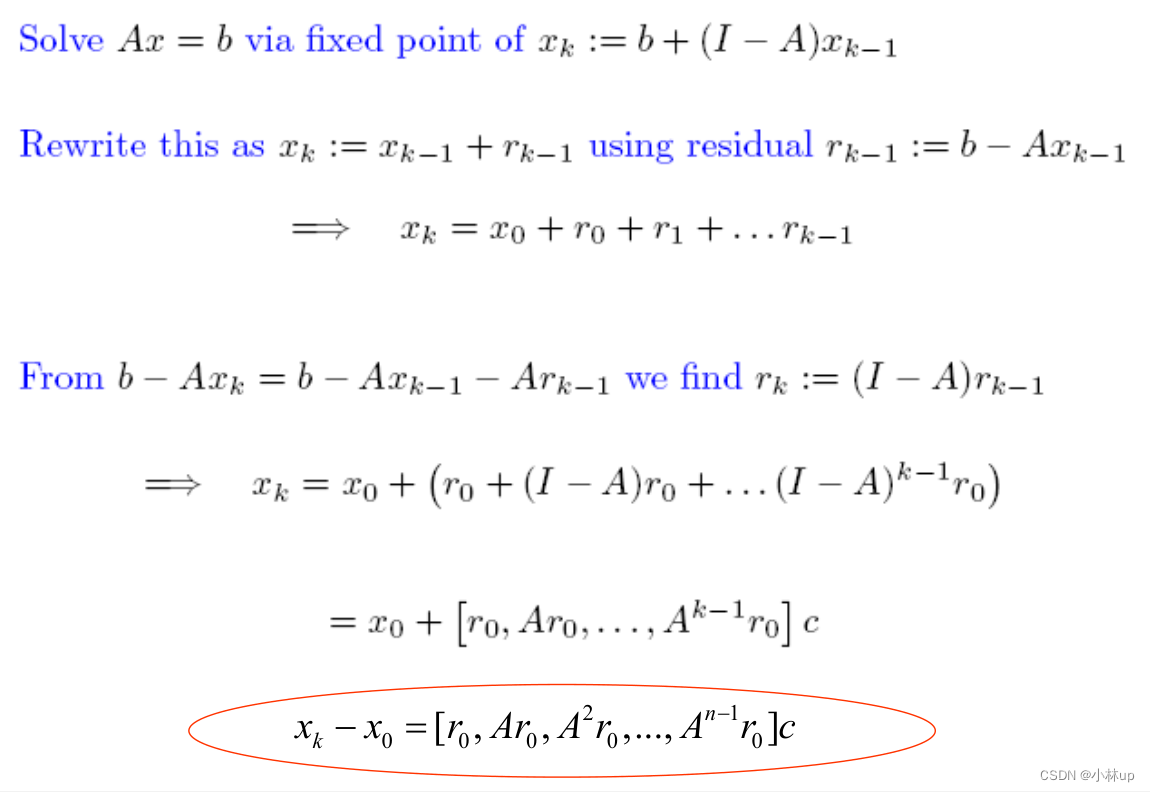
给定
x0=0xn=[b,Ab,A2b,…,An−1b]c~\\begin{array}{l} x_{0}=0 \\\\ x_{n}=\\left[b, A b, A^{2} b, \\ldots, A^{n-1} b\\right] \\tilde{c} \\end{array}x0=0xn=[b,Ab,A2b,…,An−1b]c~
xnx_{n}xn和x∗x^*x∗落在一个空间,但可能不是一个很好的近似。

 (这个图有点不清楚,后面有空改一下)
(这个图有点不清楚,后面有空改一下)

原问题的解罗落在于一个Krylov 空间,其维数是AAA的最小多项式的维度。因此,如果 AAA 的最小多项式的次数较低,则空间维数可以很小。
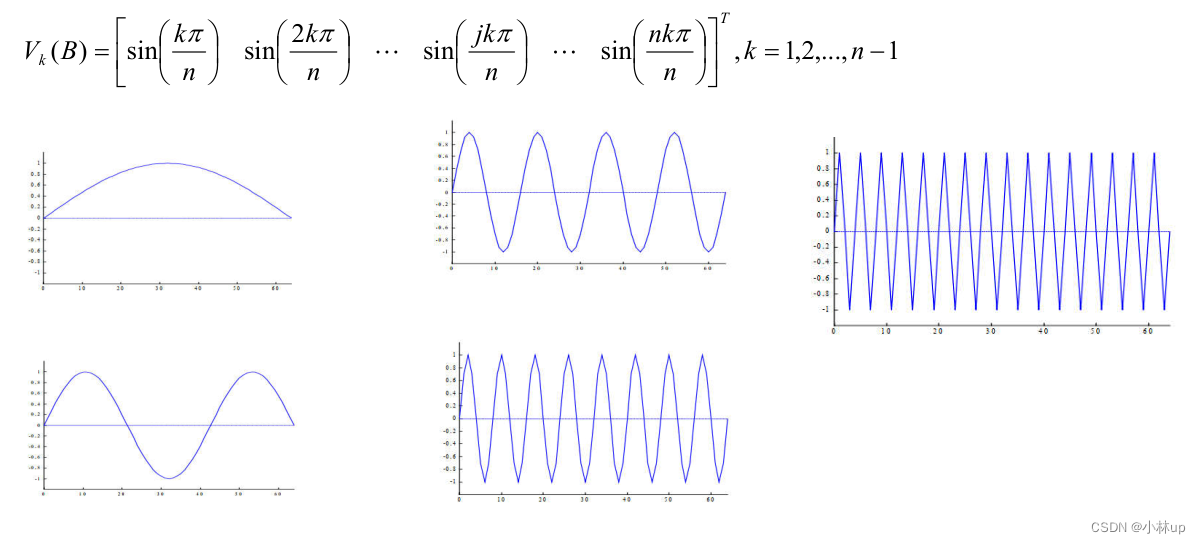
原来的空间张成向量b,Ab,A2b,⋯,An−1bb,Ab,A^2b,\\cdots,A^{n-1}bb,Ab,A2b,⋯,An−1b不正交转化为新的标准正交基qq,q2,⋯,qnq_q,q_2,\\cdots,q_nqq,q2,⋯,qn就有了下面的方法。
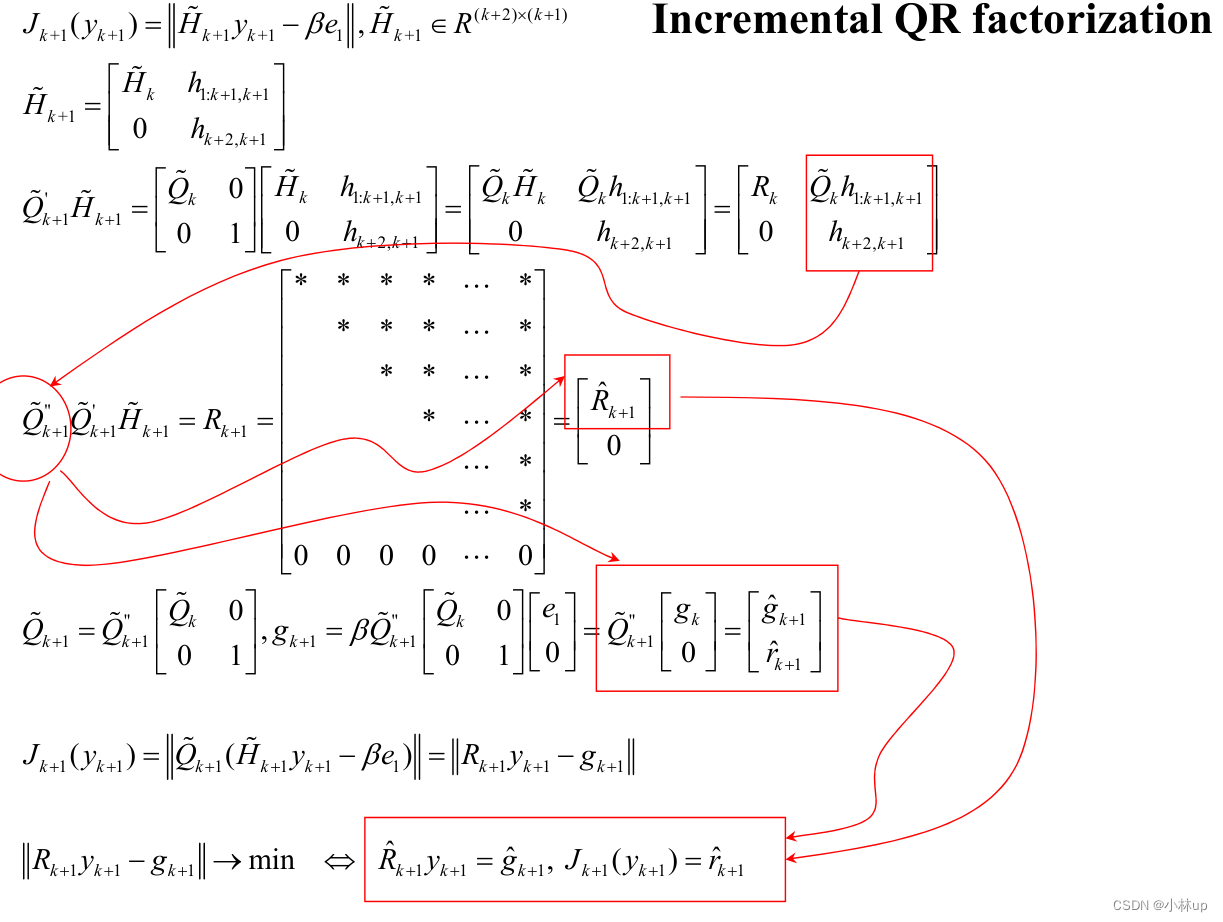
2.9 GMRES方法(Generalized Minimum Residual Method)

解释上面的第二步:
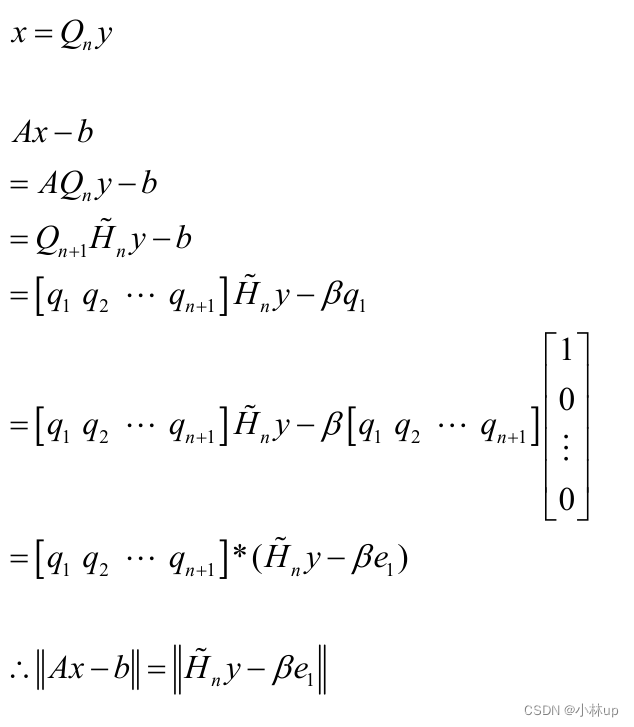

利用QR分解

3. 【线性方程组】基于优化的方法
- 若AAA是一个对称正定矩阵,下面问题等价:
Ax=b⇔minx12xTAx−bTxA x=b \\Leftrightarrow \\min _{x} \\frac{1}{2} x^{T} A x-b^{T} xAx=b⇔xmin21xTAx−bTx
- 若AAA是一个大型稀疏方阵,下面问题等价:
Ax=b⇔minx∥Ax−b∥A x=b \\Leftrightarrow \\min _{x}\\|A x-b\\|Ax=b⇔xmin∥Ax−b∥
3.1 共轭梯度法(Conjugate gradient method【CG】)
两个向量S1S_1S1和S2S_2S2是共轭的,当它们满足S1TAS2=0S_{1}^{\\mathrm{T}} A S_{2}=0S1TAS2=0
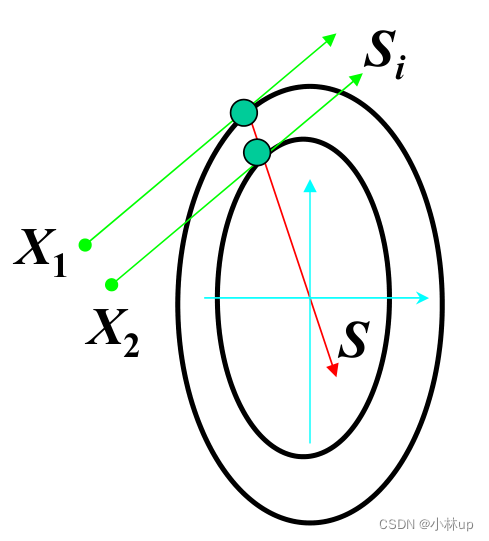
f(X)=12XTAX−bTX∇f(X)=AX−bϕ′(a1)=SiT∇f(X1+a1Si)=SiT(AX(1)−b)=0X(1)=X1+a1Siϕ′(a2)=SiT∇f(X2+a2Si)=SiT(AX(2)−b)=0X(2)=X2+a2SiSiTA(X(2)−X(1))=SiTAS=0\\begin{aligned} &f(X) = \\frac{1}{2} X^{T} A X-b^{T} X \\\\ &\\nabla f(X) = A X-b \\\\ &\\phi^{\\prime}\\left(a_{1}\\right) = S_{i}^{T} \\nabla f\\left(X_{1}+a_{1} S_{i}\\right) = S_{i}^{T}\\left(A X^{(1)}-b\\right) = 0 \\quad X^{(1)}=X_{1}+a_{1} S_{i}\\\\ &\\phi^{\\prime}\\left(a_{2}\\right) = S_{i}^{T} \\nabla f\\left(X_{2}+a_{2} S_{i}\\right) = S_{i}^{T}\\left(A X^{(2)}-b\\right) = 0 \\quad X^{(2)}=X_{2}+a_{2} S_{i}\\\\ &S_{i}^{T} A\\left(X^{(2)}-X^{(1)}\\right) = S_{i}^{T} A S = 0 \\end{aligned}f(X)=21XTAX−bTX∇f(X)=AX−bϕ′(a1)=SiT∇f(X1+a1Si)=SiT(AX(1)−b)=0X(1)=X1+a1Siϕ′(a2)=SiT∇f(X2+a2Si)=SiT(AX(2)−b)=0X(2)=X2+a2SiSiTA(X(2)−X(1))=SiTAS=0
可以有限步数收敛!
算法流程:
1.g0=∇f(x0),d0=−g0;2.When∣gk∣<eps,exit;3.ak=argminakf(xk+akdk);4.gk+1=∇f(xk+1)=∇f(xk+akdk);5.βk=gk+1Tgk+1/gkTgk;6.dk+1=−gk+1+βkdk;7.k=k+1,goto2.\\begin{aligned} &1. {g}_{0} = \\nabla f\\left({x}_{0}\\right), {d}_{{0}} = -{g}_{0} ; \\\\&2. When \\left|{g}_{{k}}\\right|<{eps} , exit; \\\\&3. a_k = \\mathop{\\arg\\min}\\limits_{a_k} {f}\\left({x}_{{k}}+a_{{k}} {d}_{{k}}\\right) ; \\\\&4. g_{{k}+1} = \\nabla f\\left({x}_{{k}+1}\\right) =\\nabla f({x}_{{k}}+a_{{k}} {d}_{{k}}); \\\\&5. \\beta_{{k}} = {g}_{{k}+1}^{{T}} {g}_{{k}+{1}} / {g}_{{k}}^{{T}} {g}_{{k}} ;\\\\ &6. d_{k+1} = -g_{k+1}+\\beta_{k} d_{k} ;\\\\ &7. k = k+1 , go \\,\\,to\\,\\, 2 . \\end{aligned}1.g0=∇f(x0),d0=−g0;2.When∣gk∣<eps,exit;3.ak=akargminf(xk+akdk);4.gk+1=∇f(xk+1)=∇f(xk+akdk);5.βk=gk+1Tgk+1/gkTgk;6.dk+1=−gk+1+βkdk;7.k=k+1,goto2.
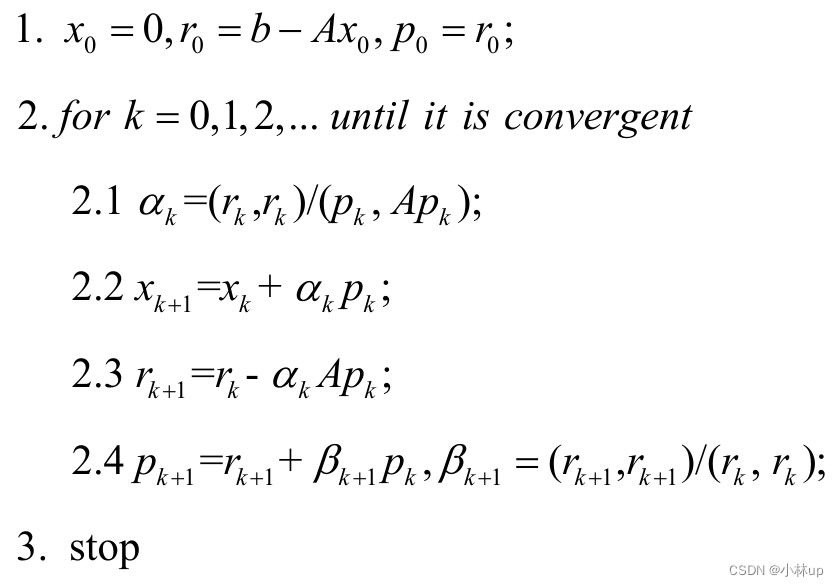
共轭梯度法(CG)特点:
①有限次收敛迭代
②计算复杂度O(n3)O(n^3)O(n3),如果矩阵AAA是一个对角矩阵,计算复杂度下降为O(ωn2)O(\\omega n^2)O(ωn2)
3.2 共轭梯度法和其他算法的对比
共轭梯度法(CG) vs 高斯消元
①CG在所有有限步数之前可以得到足够精确的解
②CG保证稀疏性,即使AAA不是对角阵。
共轭梯度法 vs 迭代方法
①CG保证收敛.
②收敛速度不同。
∥x(k+1)−x∗∥A<C∥x(k)−x∗∥A,C=cond(A)−1cond(A)+1,∥x∥A=xTAx\\left\\|x^{(k+1)}-x^{*}\\right\\|_{A}<C\\left\\|x^{(k)}-x^{*}\\right\\|_{A}, C=\\frac{\\sqrt{\\operatorname{cond}(A)}-1}{\\sqrt{\\operatorname{cond}(A)}+1},\\|x\\|_{A}=\\sqrt{x^{T} A x}x(k+1)−x∗A<Cx(k)−x∗A,C=cond(A)+1cond(A)−1,∥x∥A=xTAx
3.3 预条件共轭梯度法(Preconditioned conjugate gradient method)
在1.3我们讲到了条件数,预条件共轭梯度法就是想办法找到合适的A~\\tilde{A}A~降低条件数的大小,提高解的稳定性。
我们这样构造A~\\tilde{A}A~以及x~\\tilde{x}x~和b~\\tilde{b}b~
A~=C−1AC−T,x~=CTx,b~=C−1b\\tilde{A}=C^{-1} A C^{-T}, \\tilde{x}=C^{T} x,\\tilde{b}=C^{-1} bA~=C−1AC−T,x~=CTx,b~=C−1b
于是有:
Ax=b⇔A~x~=b~A x=b \\Leftrightarrow \\tilde{A} \\tilde{x}=\\tilde{b}Ax=b⇔A~x~=b~
我们可以验证:
cond2(A~)<cond2(A)cond2(A)=∣λmax∣∣λmin∣{cond}_{2}(\\tilde A)<{cond}_{2}(A)\\quad {cond}_{2}(A)=\\frac{\\left|\\lambda_{\\max }\\right|}{\\left|\\lambda_{\\min }\\right|}cond2(A~)<cond2(A)cond2(A)=∣λmin∣∣λmax∣
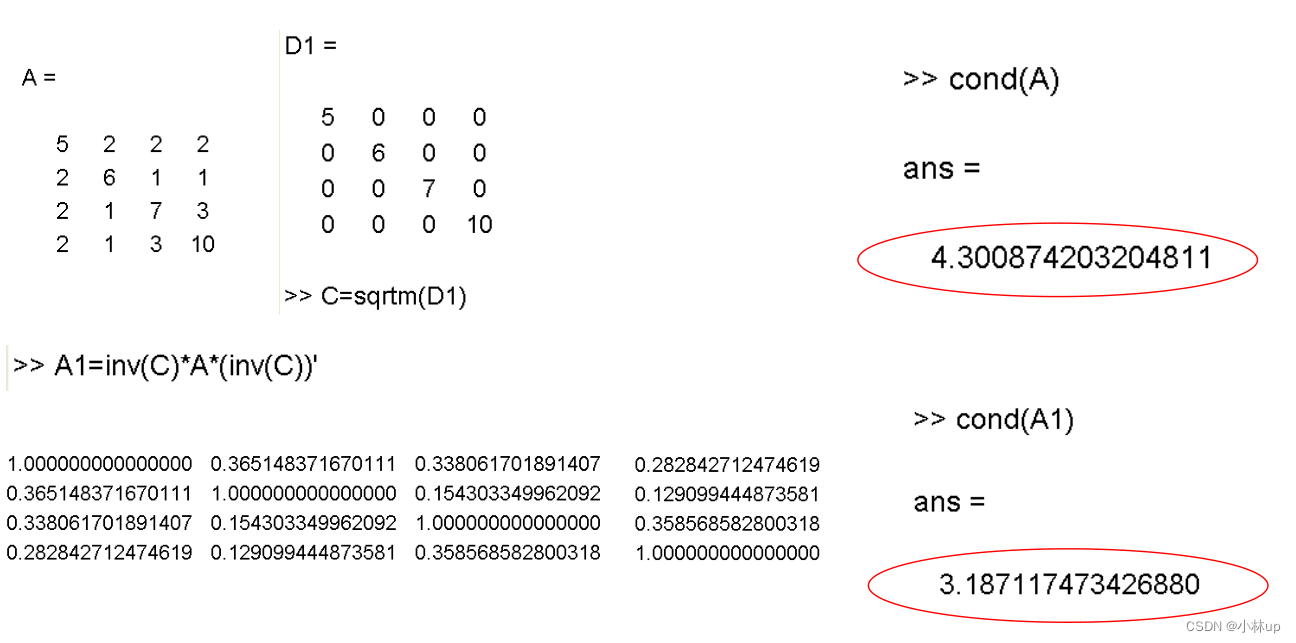
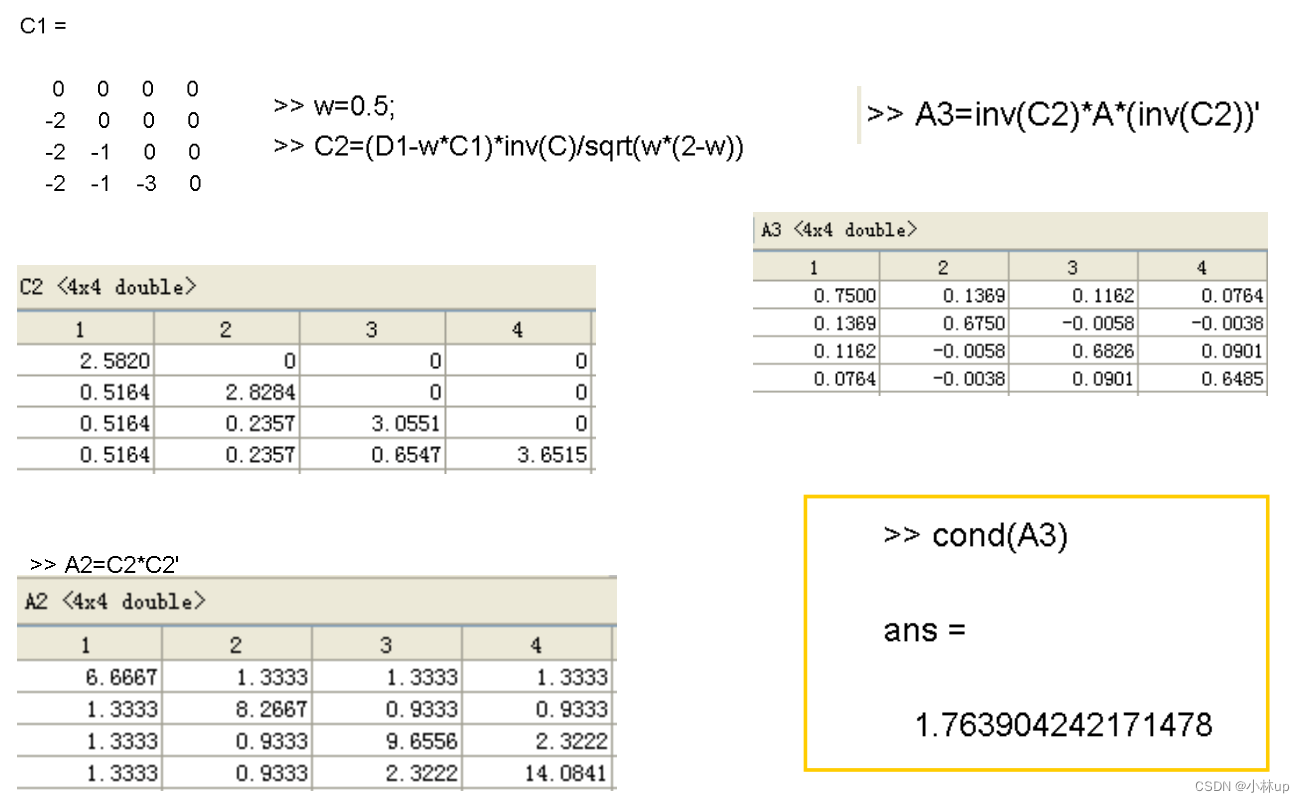
- 按照下面的方式取定CCC,条件数变小了【这一块没写清楚,回头再写写补坑】
C−1=D−1/2,D=diag(a11,a22,…,ann),A=(aij)n×nC^{-1}=D^{-1 / 2}, D=\\operatorname{diag}\\left(a_{11}, a_{22}, \\ldots, a_{n n}\\right), A=\\left(a_{i j}\\right)_{n \\times n}C−1=D−1/2,D=diag(a11,a22,…,ann),A=(aij)n×n
2. 按照下面的方式取定CCC,条件数变小了
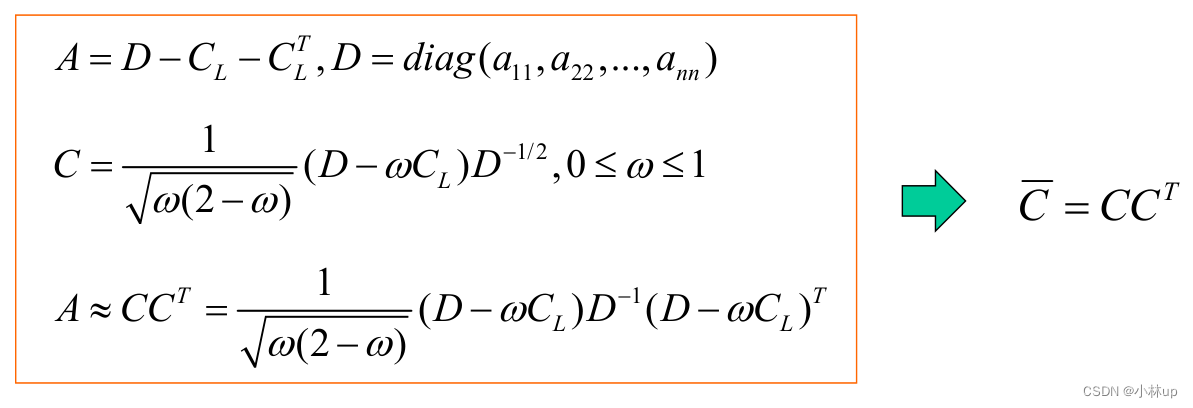
预条件共轭梯度法算法流程:
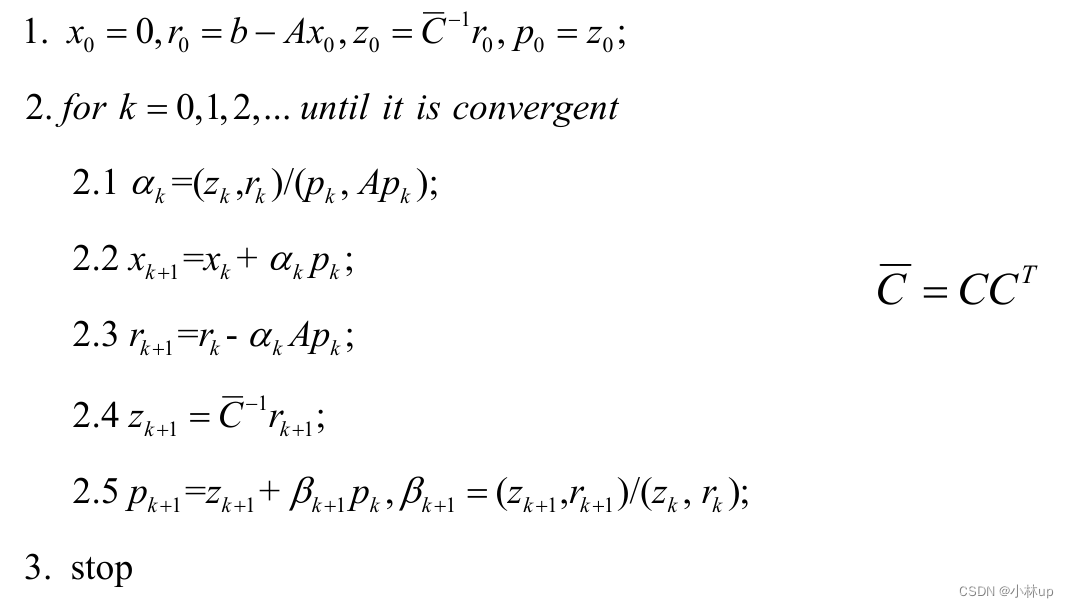
4. 【非线性方程组】Jacobian矩阵、Newton迭代法、不动点迭代法、Seidel迭代法
4.1 Jacobian矩阵
针对一个非线性方程组,可能有无穷多解。利用Jacobian矩阵迭代线性化处理变为求解线性方程组。
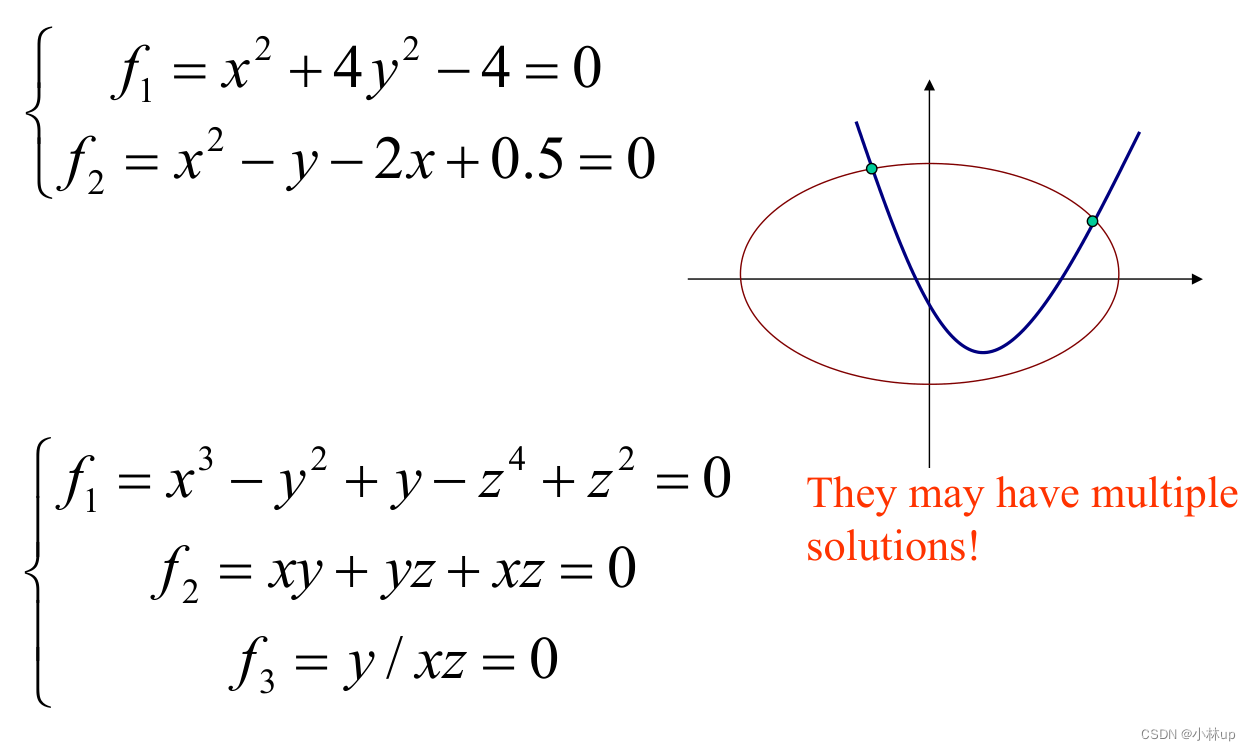


利用Jacobian矩阵引出Newton方法:
4.2 Newton迭代法

算法流程

Jacobian矩阵的问题
①出现奇异,内部元素分母为0或矩阵的秩为0
②收敛阶数降低
③有不确定性
4.3 不动点迭代法

假设 gig_igi 的偏导数在包含不动点 (p,q,r)(p,q,r)(p,q,r)的一个区域上是连续的。如果选择的起点足够接近定点,并且
∣∂g1∂x(p,q,r)∣+∣∂g1∂y(p,q,r)∣+∣∂g1∂z(p,q,r)∣<1,∣∂g2∂x(p,q,r)∣+∣∂g2∂y(p,q,r)∣+∣∂g2∂z(p,q,r)∣<1,∣∂g3∂x(p,q,r)∣+∣∂g3∂y(p,q,r)∣+∣∂g3∂z(p,q,r)∣<1,\\begin{array}{l} \\left|\\frac{\\partial g_{1}}{\\partial x}(p, q, r)\\right|+\\left|\\frac{\\partial g_{1}}{\\partial y}(p, q, r)\\right|+\\left|\\frac{\\partial g_{1}}{\\partial z}(p, q, r)\\right|<1, \\\\ \\left|\\frac{\\partial g_{2}}{\\partial x}(p, q, r)\\right|+\\left|\\frac{\\partial g_{2}}{\\partial y}(p, q, r)\\right|+\\left|\\frac{\\partial g_{2}}{\\partial z}(p, q, r)\\right|<1, \\\\ \\left|\\frac{\\partial g_{3}}{\\partial x}(p, q, r)\\right|+\\left|\\frac{\\partial g_{3}}{\\partial y}(p, q, r)\\right|+\\left|\\frac{\\partial g_{3}}{\\partial z}(p, q, r)\\right|<1, \\end{array}∂x∂g1(p,q,r)+∂y∂g1(p,q,r)+∂z∂g1(p,q,r)<1,∂x∂g2(p,q,r)+∂y∂g2(p,q,r)+∂z∂g2(p,q,r)<1,∂x∂g3(p,q,r)+∂y∂g3(p,q,r)+∂z∂g3(p,q,r)<1,
这意味着ρ(J)≤∥J∥∞<1\\rho(J) \\leq\\|J\\|_{\\infty}<1ρ(J)≤∥J∥∞<1。
那么不动点迭代收敛到定点。
4.4 Seidel迭代法

5. Matlab相关函数