PS：贪心算法整一个大章节跳过了，过后两天补上。今天先跟上动态规划的步伐。

总链接：第九章 动态规划part01

动态规划基础

 打家劫舍3道，股票问题7、8道。

关键点：

1、找dp数组，下标的表示含义，一定要清楚dp[i][j]中i,j,的含义。

2、递推公式

3、dp数组如何初始化

4、遍历顺序

5、当自己感到迷惑时，要打印dp数组。

509. 斐波那契数

很简单的动规入门题，但简单题使用来掌握方法论的，还是要有动规五部曲来分析。

链接：代码随想录

自己的解法：

class Solution {
public:int fib(int n) {int a=0;int b=1;while(n>0){int temp=a;a=a+b;b=temp;n--;}return a;}
};

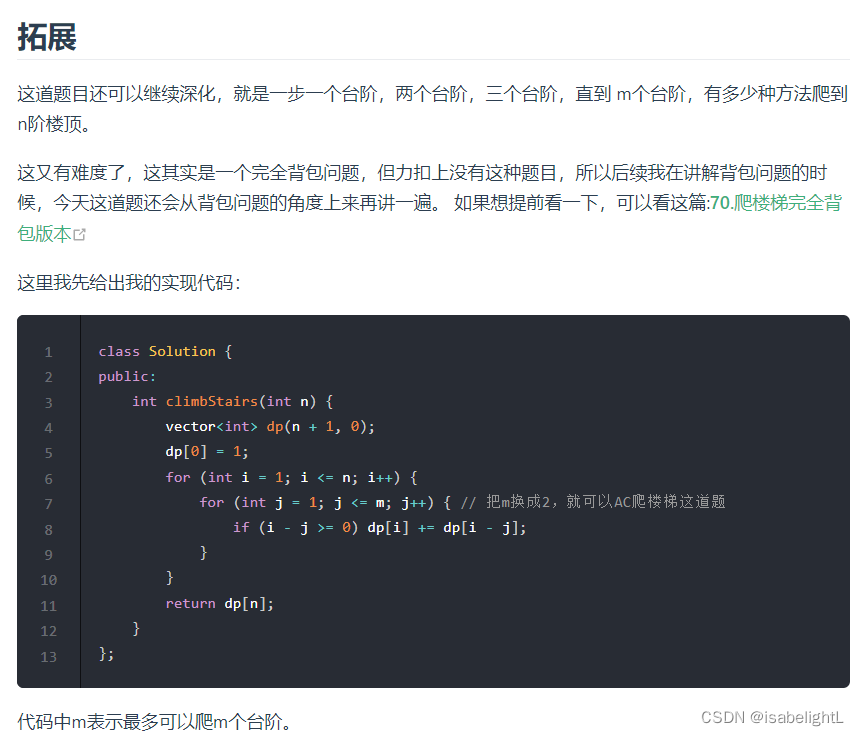
70. 爬楼梯

链接：代码随想录

 

class Solution {
public:
/*考虑最后一步dp[i] 代表到达第i节的爬法有dp[i]种，则：dp[i]=d[i-1]+dp[i-2]*/int climbStairs(int n) {vector<int>dp(n+1,0);dp[0]=1;dp[1]=1;int i=2;while(i<=n){dp[i]=dp[i-1]+dp[i-2];i++;}return dp[n];}
};

 有拓展问题，但是没有看

 

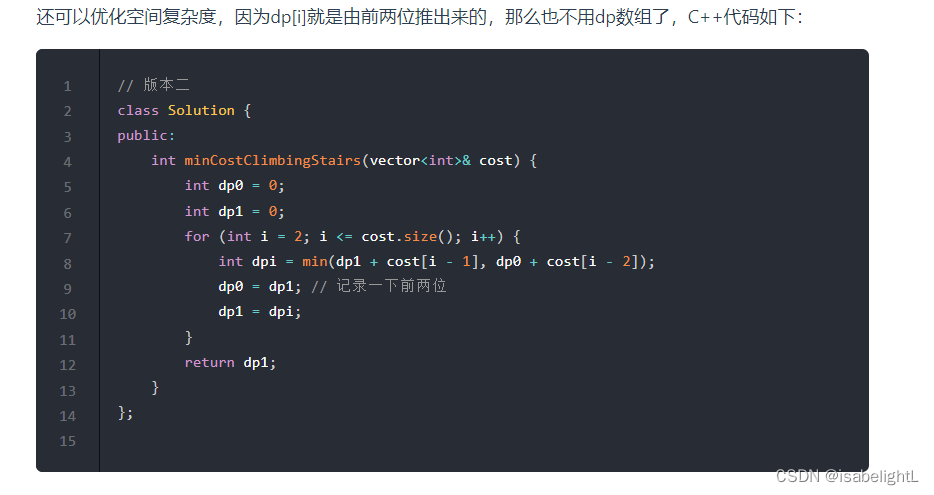
746. 使用最小花费爬楼梯

链接：代码随想录

 

 

class Solution {
/*
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
结合爬楼梯那道题来看，
*/
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int>dp(n+1,0);dp[0]=0;dp[1]=0;/*dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cos[i-2]);*/for(int i=2;i<n+1;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]); }return dp[n];}
};