网站导航
> 文章列表 > 数学分析：多元微积分4

数学分析：多元微积分4

网友: 文章列表 2024-03-21 19:25:49

数学分析：多元微积分4

再看多元微分的泰勒公式前，我们回忆下泰勒公式的初始意义：

根据数学分析1 150页。

其实是用多项式去逼近具体函数f(x)的过程。

现在，我们来看多元微分的泰勒公式：

再看这个公式之前，我们需要引入这样一个问题：

这是一个复合函数，R空间下的t，

然后s(t) = x + th, s是R^n空间下的。最后是f(s(t))

所以是R-->R^n--->R的一个函数。于是f对t求导，就应该是

(\\partial _{s1}f, \\partial _{s2}f) \\begin{pmatrix} ds_1/dt\\\\ ds_2/dt \\end{pmatrix}=\\partial _{s1}f ds1/dt + \\partial _{s2}f ds2/dt

s=(s1,s2)=(x^1+th^1,x^2+th^2)

\\partial \\partial _1f(s1,s2)h^1=h^1\\partial _{11}fh^1 + h^1\\partial _{21}fh^2

同理：

\\partial \\partial _2f(s1,s2)h^2=h^2\\partial _{12}fh^1 + h^2\\partial _{22}fh^2

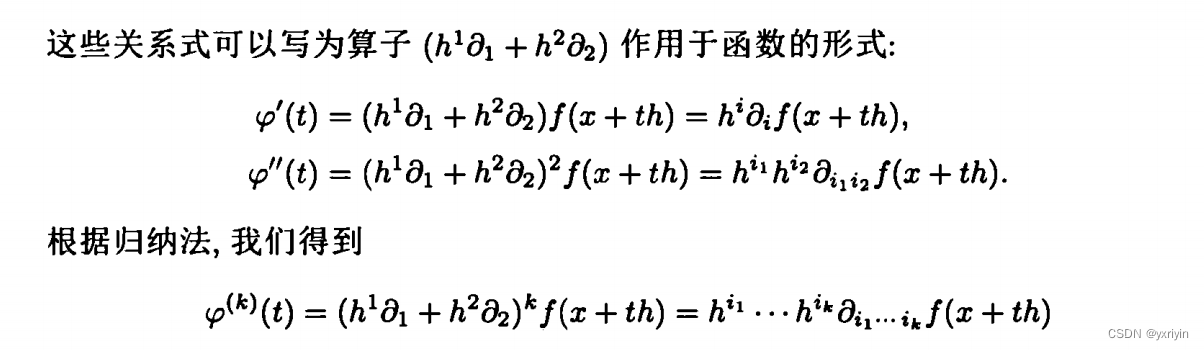
这个后面的简写有点难理解，尝试写成求和公式：

\\sum_{i=1}^{2}h^i\\sum_{j=1}^{2}h^j\\partial _{ij}=\\sum_{i=1}^{2}h^i(h^1\\partial _{i1} + h^2\\partial {i2})= h^1(h^1\\partial _{11} + h^2\\partial _{12}) + h^2(h^1\\partial _{21} + h^2\\partial _{22})

确实一样

回到泰勒公式的证明：

 

 

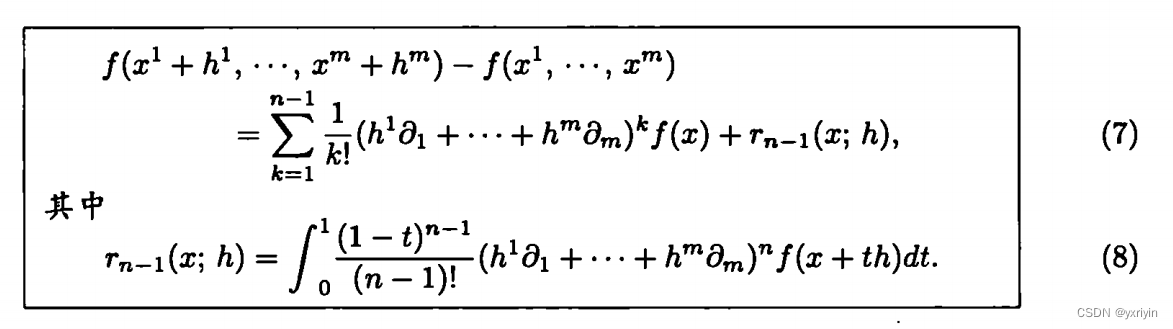
 接下来是非常重要的定理：

 

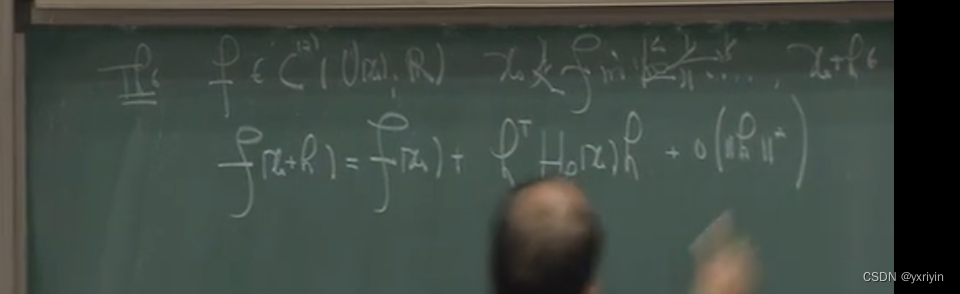
二次型可以写成一个矩阵：

(h_1,h_2)\\begin{pmatrix} \\partial _{11}f &\\partial _{21}f \\\\ \\partial _{12}f & \\partial _{22}f \\end{pmatrix}\\begin{pmatrix} h_1\\\\h_2 \\end{pmatrix}=(h1,h2)\\begin{pmatrix} \\partial _{11}fh^1 + \\partial _{21}fh^2\\\\ \\partial _{12}fh^1 + \\partial _{22}fh^2 \\end{pmatrix}=(\\partial _1h^1 + \\partial _2h^2)^2f

这里要注意，16其实是表示前面的

 (h_1,h_2)\\begin{pmatrix} \\partial _{11}f &\\partial _{21}f \\\\ \\partial _{12}f & \\partial _{22}f \\end{pmatrix}\\begin{pmatrix} h_1\\\\h_2 \\end{pmatrix}化成了单位矩阵

变成了e^THe,它在R^m中连续，也在R^m-1维的球面上连续。这里其实有点难理解，用了一个技巧，它把所有的h里的分量进行了归一化，然后把|h|提取到前面。然后因为我们只关心前面的正负号，所以可以忽视被提取出去的项。而归一化后的变量，可以看成一个在球面上的紧集。这里要注意，其实它把不确定性给提取出去了，本来这可能是一个无穷的，但是现在变成了 一个无穷的*有界集。

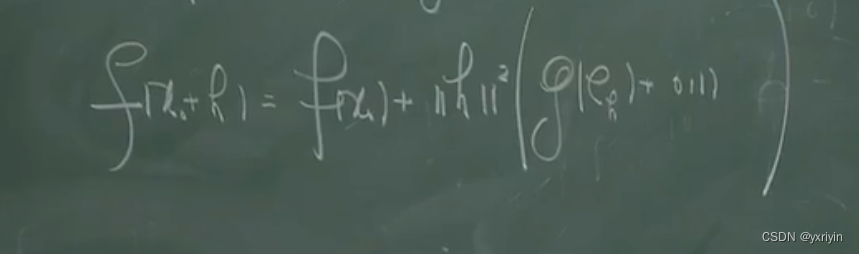
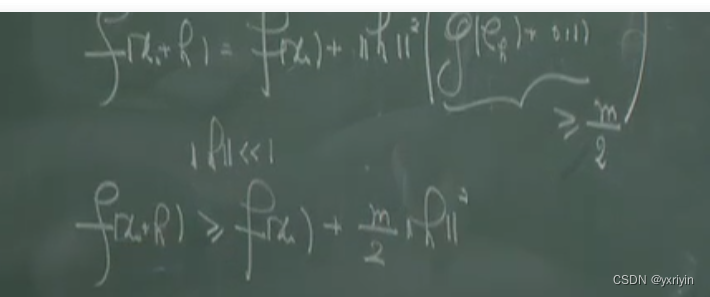
 老师的证明更加清晰。

这个部分我们在后续的线性代数进阶中继续学习。

网络标签：

相关问题