LeetCode-120. 三角形最小路径和

题目来源
120. 三角形最小路径和

题目思路

由上往下

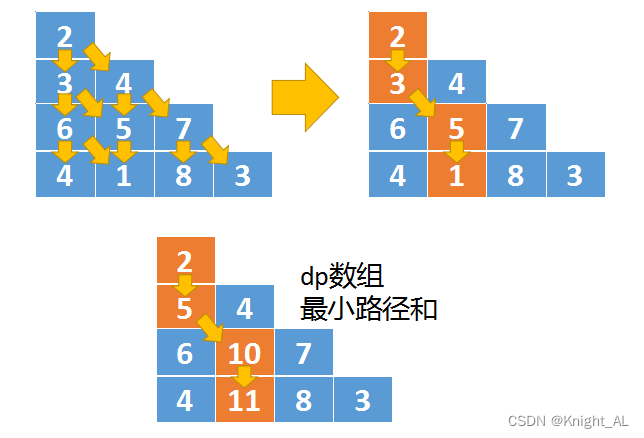
动态规划(由上到下)

• 1.确定dp数组以及下标的含义

dp[i][j] 表示从点 (i,j)) 到底边的最小路径和。

• 2.确定递推公式

常规： triangle[i][j]一定会经过triangle[i-1][j]或者triangle[i-1][j-1], 所以状态dp[i][j]一定等于dp[i-1][j]或者dp[i-1][j-1]的最小值+triangle[i][j]
特殊： triangle[i][0]没有左上角 只能从triangle[i-1][j]经过 triangle[i][0]
triangle[i][row[0].length-1]没有上角 只能从triangle[i-1][j-1]经过 triangle[i][row[0].length-1]
转换方程：dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j-1])+triangle[i][j]

• 3.dp数组如何初始化

由递推公式dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j-1])+triangle[i][j]可知，我们要推前面的一个，所以dp[0][0] = triangle.get(0).get(0);

• 4.确定遍历顺序

由递推公式dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j-1])+triangle[i][j]可知，我们要推前面的一个，便利是顺序从上往下，从左到右

代码实现

class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();int[][] dp = new int[n][n];dp[0][0] = triangle.get(0).get(0);for(int i = 1;i<dp.length;i++){for(int j =0;j<=i;j++){if(j == 0){dp[i][j] = dp[i-1][j]+triangle.get(i).get(j);}else if(j==i){dp[i][j] = dp[i-1][j-1]+triangle.get(i).get(j);}else{dp[i][j] = Math.min(dp[i-1][j],dp[i-1][j-1])+triangle.get(i).get(j);}}}int minNum = Integer.MAX_VALUE;for(int i = 0;i<n;i++){minNum = Math.min(minNum,dp[n-1][i]);}return minNum;}
}

动态规划(由下到上)

这种思路的好处是上面越来越小，没有边界的特殊处理

class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();int[][] dp = new int[n+1][n+1];for(int i = n-1;i>=0;i--){for(int j = i;j>=0;j--){dp[i][j] = Math.min(dp[i+1][j],dp[i+1][j+1])+triangle.get(i).get(j);}}return dp[0][0];}
}