C++二叉搜索树与KV模型

二叉搜索树与KV模型
- 二叉搜索树
-
- 概念与操作
- 性能分析
- 实现
- KV模型
二叉搜索树
本章是为了C++的map和set做铺垫
概念与操作
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到到空,还没找到,这个值不存在。
二叉搜索树的插入
a. 树为空,则直接新增节点,赋值给root指针。
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点。
其实上面两个还是很容易实现的,最难的是删除这里,要考虑三种情况:
删除的是叶子结点,那就找到直接释放就好了。
删除的是只有一个左/右孩子的结点,那就先链接父亲结点和左/右孩子结点,然后直接删除该节点。
其实删除叶子结点可以和删除一个孩子结点的合并,因为叶子节点两个都是空,删除一个孩子的结点只有一个是空。
删除两个孩子结点的最麻烦,首先要找到替换这个结点的值,肯定是左子树最大的或者是右子树最小的。(二选一都可以,这里我选择左子树最小的)
性能分析
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
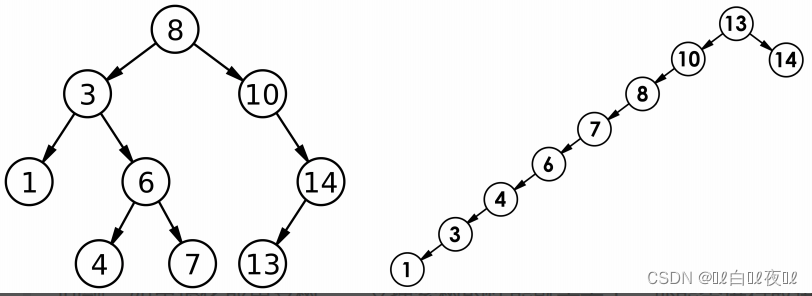
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log2Nlog_2 Nlog2N
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N2\\frac{N}{2}2N
其实二叉搜索树是一个不完整的树,遇到这种极端情况就没有办了,后面的AVL和红黑树会完成这个功能。
实现
实现这里我会写出某些成员函数的递归与迭代版本。
其实最难的是删除步骤:
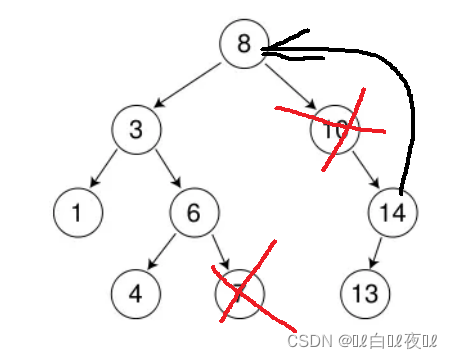
如果是删除叶子结点直接删除就可以,只有一个孩子的就先看是只有左孩子还是只右有孩子,如果只有左孩子就让父节点的指针指向左孩子,如果只有右孩子就让父亲的指针指向右孩子,然后判断要删除的结点在父节点的左子树还是右子树,才能判断让父节点的左指针还是右指针去链接孩子。
但是这个思路还要考虑这种情况:
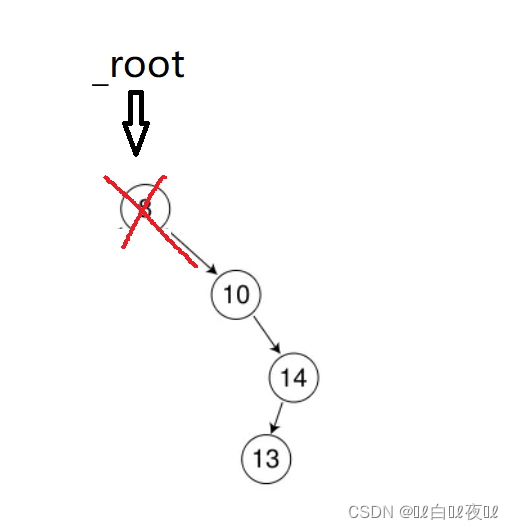
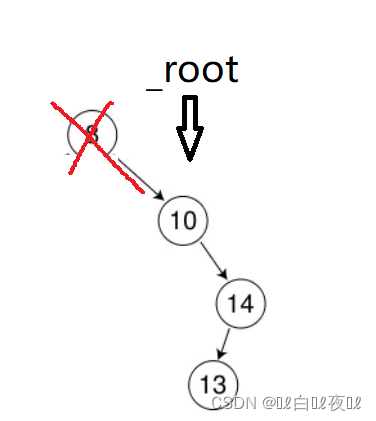
如果删除了根节点,那么就要换根。
如果是有两个孩子的就非常难办了,首先要去替换,这里用左子树的最小节点去替换。
先来看看第一种情况:
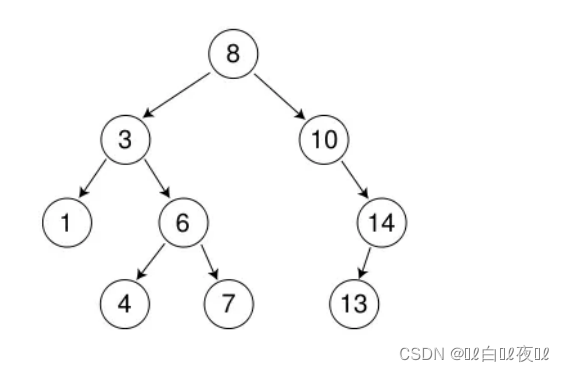
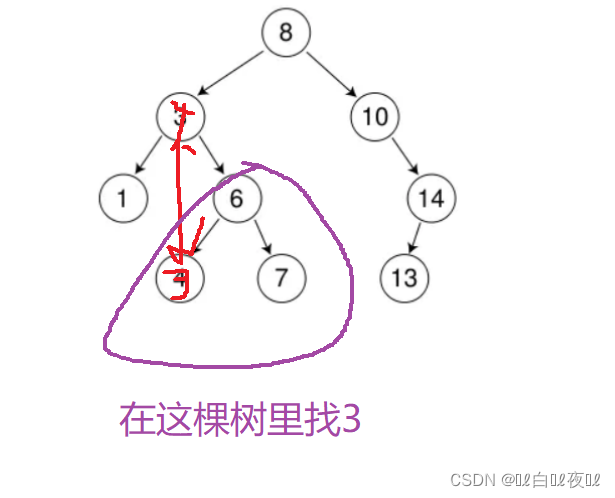
删除3,首先让3和左子树的最小值4交换(赋值也行),然后让cur记住原来是3这里,再来一个指针记录原来是4这里,再用parent指向父节点6的位置:
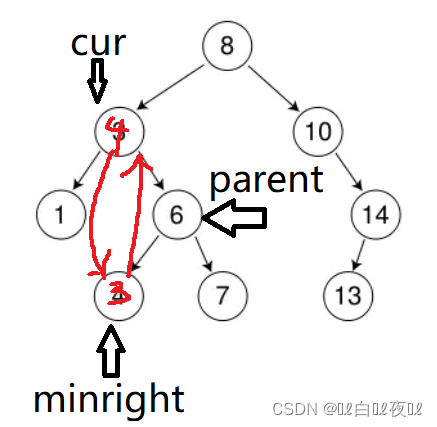
然后删除minright之前,将parent的左指针指向minright的右指针,因为minright左指针肯定是没有值了,但是右指针不一定没有。
然后是第二种情况:
删除的是根,这里只能和10交换,parent就是根,10就是minright,释放minright之前要将parent的右与minright的右链接起来。
迭代
#include<iostream>
#include<vector>
using namespace std;
template<class K>
struct BSTNode//树结点
{BSTNode(K key):_key(key),left(nullptr),right(nullptr){}K _key;//结点值BSTNode<K>* left;//左子树BSTNode<K>* right;//右子树
};
template<class K>
class BSTree//树
{typedef BSTNode<K> Node;
public:BSTree():_root(nullptr){}bool Insert(const K& key)//插入数据{if (_root == nullptr){_root = new Node(key);return true;}Node* cur = _root;Node* parent = cur;while (cur)//不等于空就一直找适合插入的位置{if (cur->_key < key){parent = cur;cur = cur->right;}else if (cur->_key > key){parent = cur;cur = cur->left;}elsereturn false;}cur = new Node(key);if (parent->_key > key)parent->left = cur;elseparent->right = cur;return true;}bool Find(const K& key)//查找{Node* cur = _root;if (cur == nullptr){return false;}while (cur){if (cur->_key > key)cur = cur->left;else if (cur ->_key < key)cur = cur->right;else{return true;}}return false;}bool Erase(const K& key)//删除数据{if (_root == nullptr){return false;}Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key < key){parent = cur;cur = cur->right;}else if (cur->_key > key){parent = cur;cur = cur->left;}else{if (cur->left == nullptr)//只有右孩子{if (cur == _root){_root = cur->right;}else if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}delete cur;//释放结点}else if (cur->right == nullptr)//只有左孩子{if (cur == _root){_root = cur->left;}else if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}delete cur;//释放结点}else//有两个孩子{Node* minright = cur->right;parent = cur;while (minright->left)//找到右子树最小值{parent = minright;minright = minright->left;}//赋值cur->_key = minright->_key;//链接if (parent->left == minright)parent->left = minright->right;elseparent->right = minright->right;delete minright;}return true;}}return false;}void _InOrder()//因为不想让外界访问道内部的_root,所以只能通过成员函数内部访问{InOrder(_root);cout << endl;}
private:void InOrder(Node* root)//中序遍历{if (root == nullptr){return;}InOrder(root->left);cout << root->_key << ' ';InOrder(root->right);}Node* _root;//树的根结点
};
递归
递归的函数都要带头结点,也就是说又要去调用子函数的方式来调用对应的递归函数。
查找:
bool FindR(Node* root, const K& key)//记得传头结点
{if (root == nullptr)return false;if (root->_key < key){return FindR(root->right, key);}else if (root->_key > key){return FindR(root->left, key);}elsereturn true;
}
递归这里有些地方很巧妙:
插入:
bool InsertR(Node*& root, const K& key)//这里的root用了引用
{if (_root == nullptr){_root = new Node(key);return true;}if (_root->_key < key)InsertR(_root->right, key);else if (_root->_key > key)InsertR(_root->left, key);elsereturn false;
}
为什么这里的头结点用了引用呢?是因为解决链接问题的:
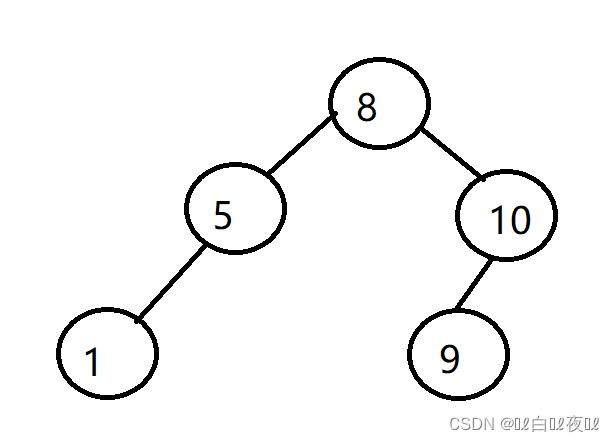
假设这里插入了一个6,应该是在5的右孩子那里,当我们找到位置的时候,上一层传递的是5的右指针,用了引用就是5的右指针的别名,开辟空间之后直接让5的右指针就能指向这块空间。
删除:
bool EraseR(Node*& root, const K& key)
{if (root == nullptr)return false;if (root->_key > key)return EraseR(root->left, key);else if (root->_key < key)return EraseR(root->right, key);else{Node* cur = root;if (root->right == nullptr)//只有左孩子{root = root->left;//这里不仅仅找到的是key,也是父节点指向该节点的指针别名}else if (root->left == nullptr)//只有右孩子{root = root->right;//这里也不用担心删除的是根,直接就将_root指向了下一个结点}else//有两个孩子,这里的引用root就不管用了,因为引用不能改指向,在这里往下找右树最小值是行不通的{Node* parent = root->right;//去该节点的右子树查找最小值while (parent->left){parent = parent->left;}swap(parent->_key, root->_key);//交换两个值return EraseR(root->right, key);//再次去找该节点最小值,也就是被交换的值,然后进行删除}delete cur;return true;}return false;
}
析构
void Destroy(Node* root){if (root == nullptr)return;Destroy(root->left);Destroy(root->right);delete root;}
拷贝
拷贝函数不能去一个一个插入:
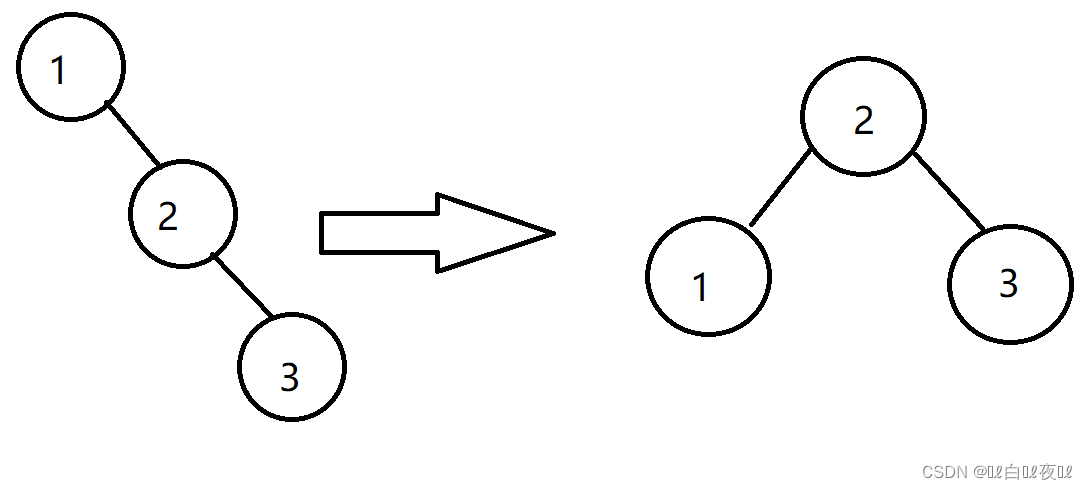
所以说,这里只要去前序遍历,然后遇到一个结点拷贝一个结点就可以了。
Node* Copy(Node* root)
{if (root == nullptr)return nullptr;Node* cur = new Node(root->_key);cur->left = Copy(root->left);cur->right = Copy(root->right);return cur;//这里将新开辟的结点返回给上一层,让上一层的指针指向这里,就能连接起来
}
KV模型
KV模型前身还有一个K(key)模型,就是上面的搜索二叉树,比如说要检查一个英语单词写的对不对,就要创建一个词库(搜索二叉树)里面找。
KV(key/value)模型是我们去查找一个英语单词的汉译,不可能在庞大的库中一个一个寻找词汇,而是通过搜索二叉树的形式寻找,那么一个单词相对应一个汉译,这个模型叫做KV模型。
其实本质就是一个结点有两个值而已。
这里的查找就很有用了,举个例子,一个学生来图书馆借书,借了多少本书需要知道,这本书归还没有也需要知道,所以这里查找也顺便进行修改。
#include<iostream>
#include<vector>
#include<string>
using namespace std;
template<class K, class V>
struct BSTNode//树结点
{BSTNode(const K& key, const V& value):_key(key),_value(value), left(nullptr), right(nullptr){}K _key;V _value;BSTNode<K, V>* left;//左子树BSTNode<K, V>* right;//右子树
};
template<class K, class V>
class BSTree//树
{typedef BSTNode<K, V> Node;
public:BSTree():_root(nullptr){}~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key, const V& value)//插入数据{if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root;Node* parent = cur;while (cur)//不等于空就一直找适合插入的位置{if (cur->_key < key){parent = cur;cur = cur->right;}else if (cur->_key > key){parent = cur;cur = cur->left;}elsereturn false;}cur = new Node(key, value);if (parent->_key > key)parent->left = cur;elseparent->right = cur;return true;}Node* Find(const K& key)//查找{Node* cur = _root;if (cur == nullptr){return nullptr;}while (cur){if (cur->_key > key)cur = cur->left;else if (cur->_key < key)cur = cur->right;else{return cur;//找到就返回该节点}}return nullptr;}bool Erase(const K& key)//删除数据{if (_root == nullptr){return false;}Node* cur = _root;Node* parent = cur;while (cur){if (cur->_key < key){parent = cur;cur = cur->right;}else if (cur->_key > key){parent = cur;cur = cur->left;}else{if (cur->left == nullptr)//只有右孩子{if (cur == _root){_root = cur->right;}else if (parent->left == cur){parent->left = cur->right;}else{parent->right = cur->right;}delete cur;//释放结点}else if (cur->right == nullptr)//只有左孩子{if (cur == _root){_root = cur->left;}else if (parent->left == cur){parent->left = cur->left;}else{parent->right = cur->left;}delete cur;//释放结点}else//有两个孩子{Node* minright = cur->right;parent = cur;while (minright->left)//找到右子树最小值{parent = minright;minright = minright->left;}//赋值cur->_key = minright->_key;//链接if (parent->left == minright)parent->left = minright->right;elseparent->right = minright->right;delete minright;}return true;}}}void _InOrder()//因为不想让外界访问道内部的_root,所以只能通过成员函数内部访问{InOrder(_root);cout << endl;}bool _FindR(const K& key){return FindR(_root, key);}
private:void Destroy(Node* root){if (root == nullptr)return;Destroy(root->left);Destroy(root->right);delete root;}void InOrder(Node* root)//中序遍历{if (root == nullptr){return;}InOrder(root->left);cout << root->_key << ' ';cout << root->_value << ' ';InOrder(root->right);}Node* _root;//树的根结点
};void test()
{BSTree<string, string> tree;tree.Insert("1", "one");tree.Insert("2", "two");tree.Insert("3", "three");tree.Insert("4", "four");tree.Insert("5", "five");BSTNode<string, string>* ret;//储存返回查找到结点的值string str;while (cin >> str){ret = tree.Find(str);if (ret)cout << ret->_value << endl;elsecout << "没有此结果" << endl;}
}