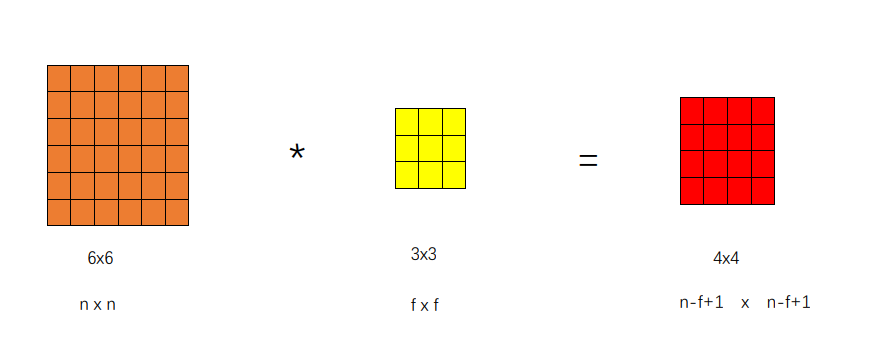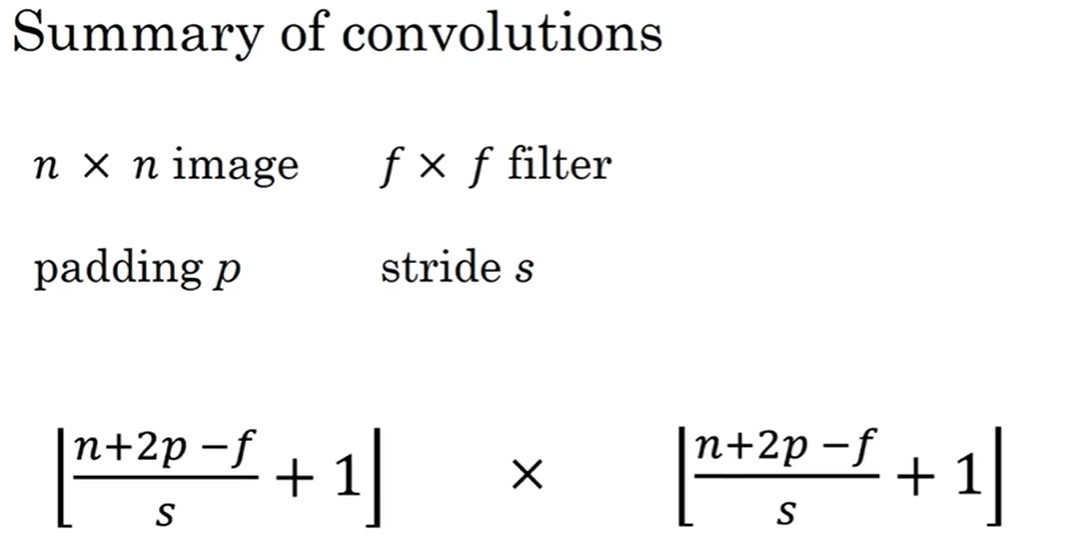【Deep Learning】CNN卷积神经网络—卷积

卷积
文章目录
- 卷积
- Quickstart
- 一,计算机视觉(Computer vision)
- 二,边缘检测(Edge detection example)
-
- -2.1 卷积操作过程:
- 三,边缘检测的更多知识(More edge detection)
- 四,填充(Padding)
-
- -4.1 卷积操作
- -4.2 填充
- -4.3 填充方式
- 五、卷积步长(Strided convolution)
-
- -5.1 步长
- -5.2 步长公式
- -5.3 卷积与交叉相关
- 六、三维卷积(Convolution over volumes)
-
- -6.1 单卷积核
- -6.2 多卷积核
- -6.3 Summary
- 七,单层卷积网络(One layer of a convolution network)
- 八、简单卷积网络示例(A simple convolution network example)
- 九、池化层(Polling)
- 十、卷积神经网络示例(Convolution neural network example)
- 十一、为什么要使用卷积(Why convolutions)
Quickstart
在本文中的"卷积"并非实际意义上的卷积,技术层面来说,应该是交叉相关(cross-correlation),而不是卷积
在信号处理或者其他数学分支领域,对卷积核进行翻转,会使卷积核保持结合律:
(A * B) * C = A * (B * C)
这一性质在信号处理领域很有用,但在深度神经网络中它并不重要
所以元素间相乘简化了代码,而且这一改变之后,不影响使用
为了方便,大多数人叫这个卷积,即使有时数学家更喜欢叫它互相关
叫法在练习中写的代码没有影响,并且对阅读文献的能力没有影响
但是在深度学习文献中,由于约定,会把交叉相关的操作称之为"卷积"
总之,在机器学习的约定中,通常忽略掉’‘翻转’'操作
技术上,我们进行的操作最好称之为交叉相关
但是,大多数深度学习的文献都叫它卷积操作
在此处也延续此称呼为卷积
一,计算机视觉(Computer vision)
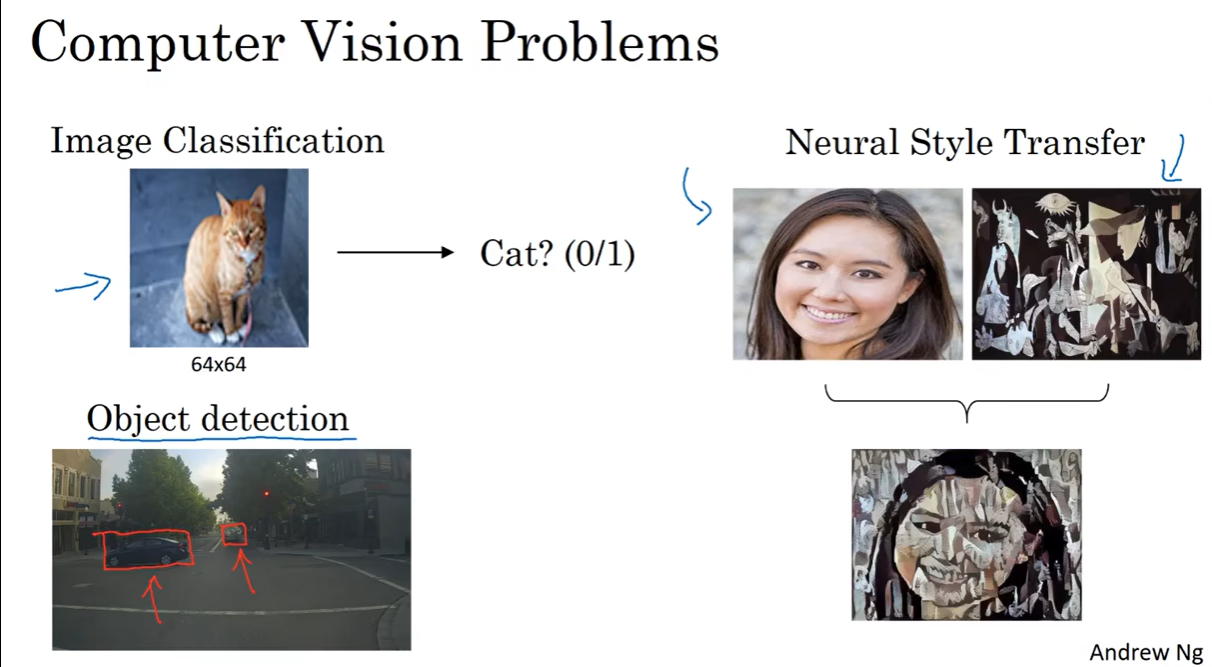
例1:图像分类,目标检测,神经风格转换
要处理的图片往往比较大,如果使用全连接神经网络,那么参数太多,计算量太大,且容易过拟合。
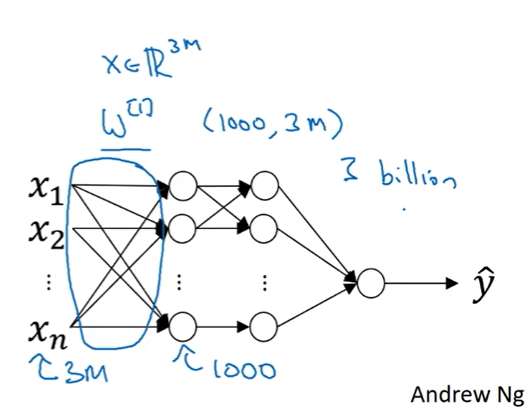
如果图片是1000*1000像素,3通道RGB,那么输入是300million,假设隐藏层有1000个神
经元,那么参数就是300millionx1000=300billion,300亿个参数,过于庞大。
因此,需要进行卷积计算。
例2:两个不同大小图片的对比
在神经网络中,如果输入的图像是1000x1000x3
他的神经网络模型将是:
二,边缘检测(Edge detection example)
例1:前几层检测边缘->后几层检测对象某些部分->更后几层检测某些整个的对象
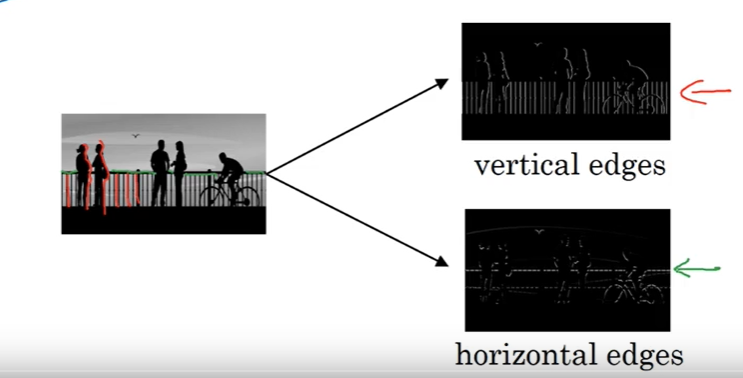
例2:检测垂直边缘和水平边缘
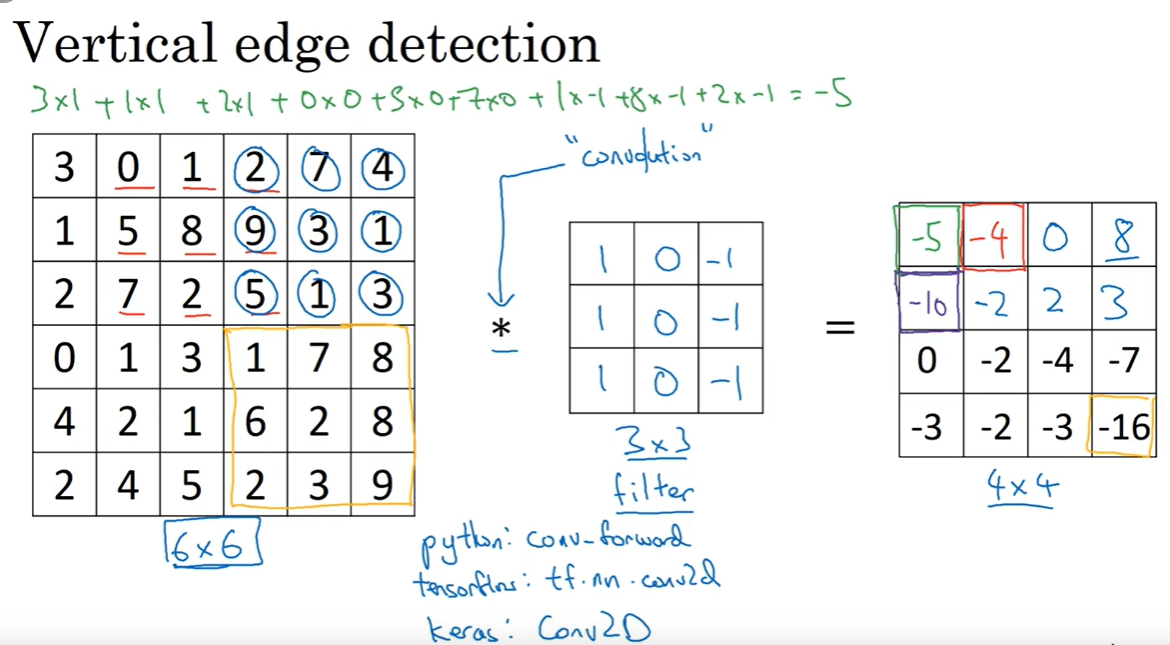
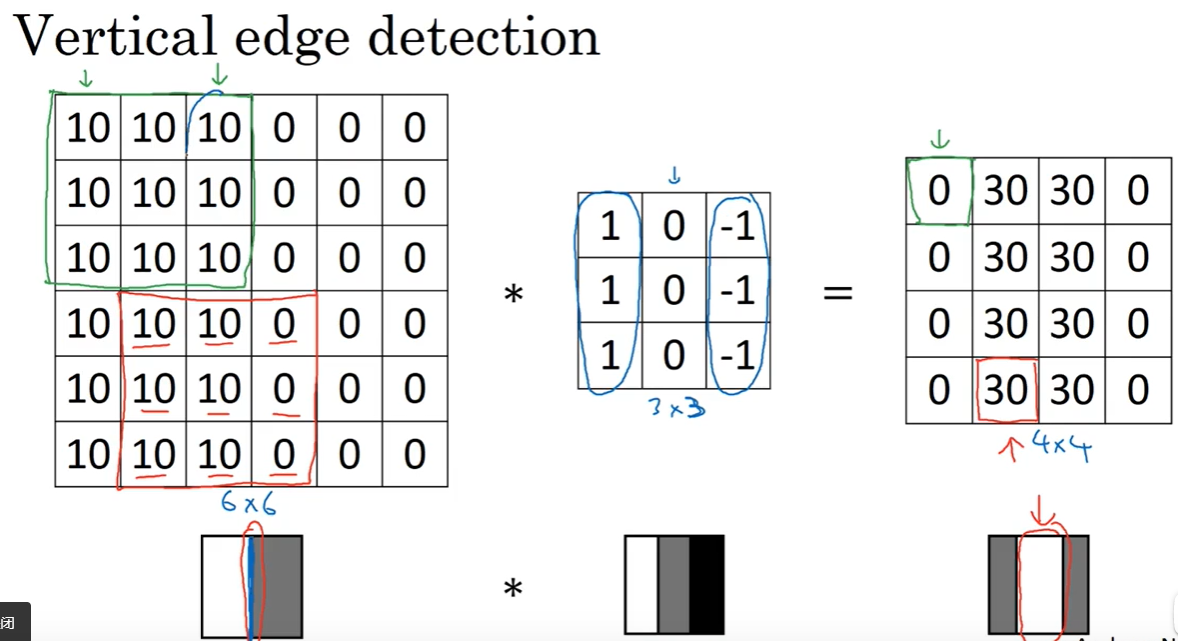
-2.1 卷积操作过程:
例3:检测垂直边缘
例4:检测垂直边缘
注:有些中文科研文章中会把fielter称作kernel
三,边缘检测的更多知识(More edge detection)
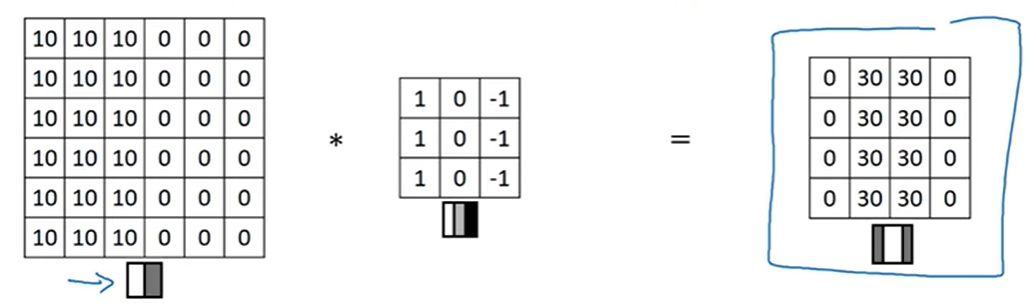
例1:垂直边缘检测
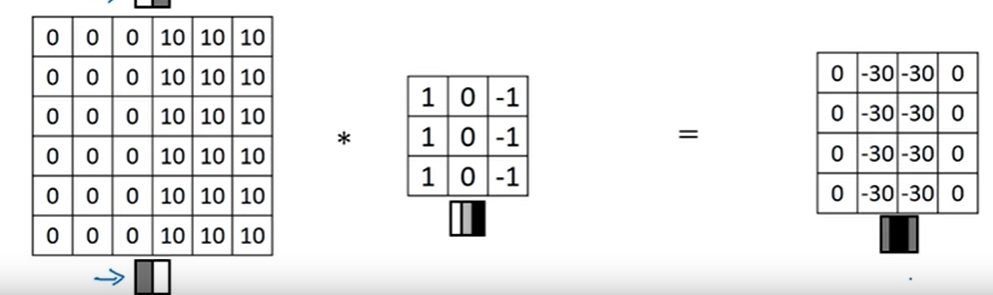
例2:反转例1数字后的垂直边缘检测
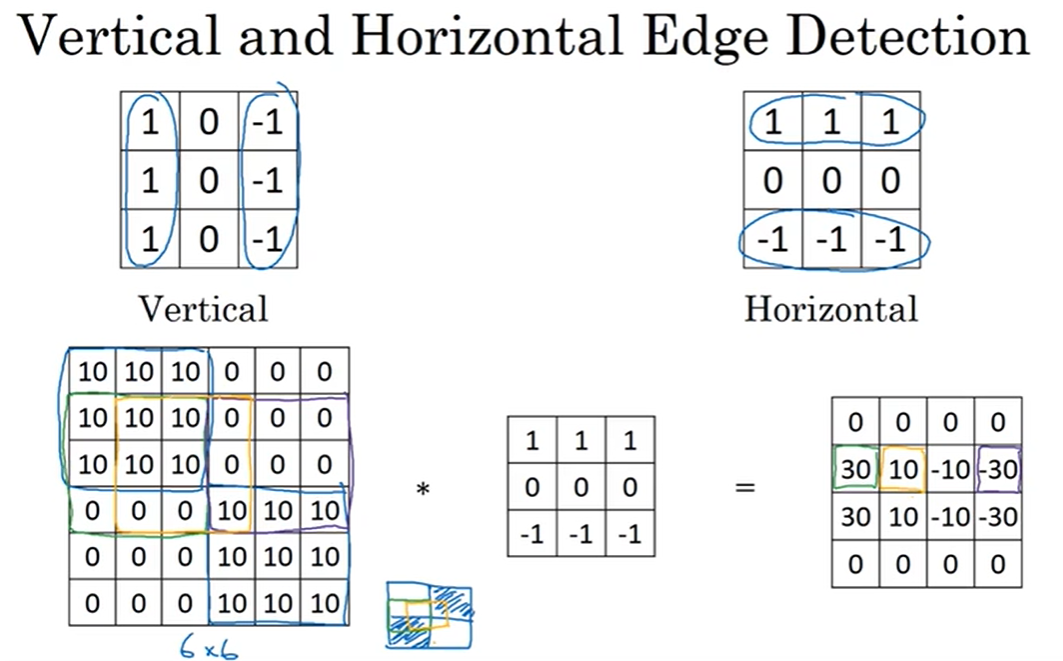
例3:水平边缘检测
总而言之,不仅可以做垂直边缘检测,也可以做水平边缘检测
而对于一个边缘检测器矩阵中,用那些数字组合是最好的仍存在争议
四,填充(Padding)
-4.1 卷积操作
例1:卷积操作:
缺点:
1:每次检测边界或者其他特征时,图片都会缩小
2:相对而言,角落或者边界上的像素被使用次数少很多,丢失了许多图片上靠近边界的信息
-4.2 填充
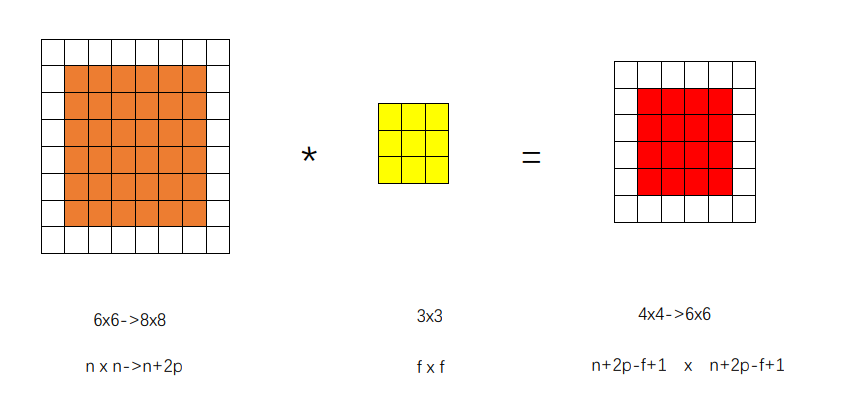
为了弥补上述两个缺点,进行padding操作。padding的字面意思是“填充”
例2:填充卷积过程:
-4.3 填充方式
两种卷积方式:
1:valid方式:不做padding
2:same方式:做padding,使得卷积操作后的图片大小与原图片大小一致。
n:原始大小
f:卷积核大小
p:padding
那么n-f+1+2p=n
p=(f-1)/2
卷积核一般用奇数,33或55或7*7的,很少有人用偶数。可能有以下两个原因:
1:奇数的话,因为padding的计算公式是需要除以2。如果是偶数,则原图片的上边缘和下边缘处理不相同。
2:奇数的话,会让卷积核有一个中心点,正中央的位置,这在图像处理过程中比较方便。
五、卷积步长(Strided convolution)
-5.1 步长
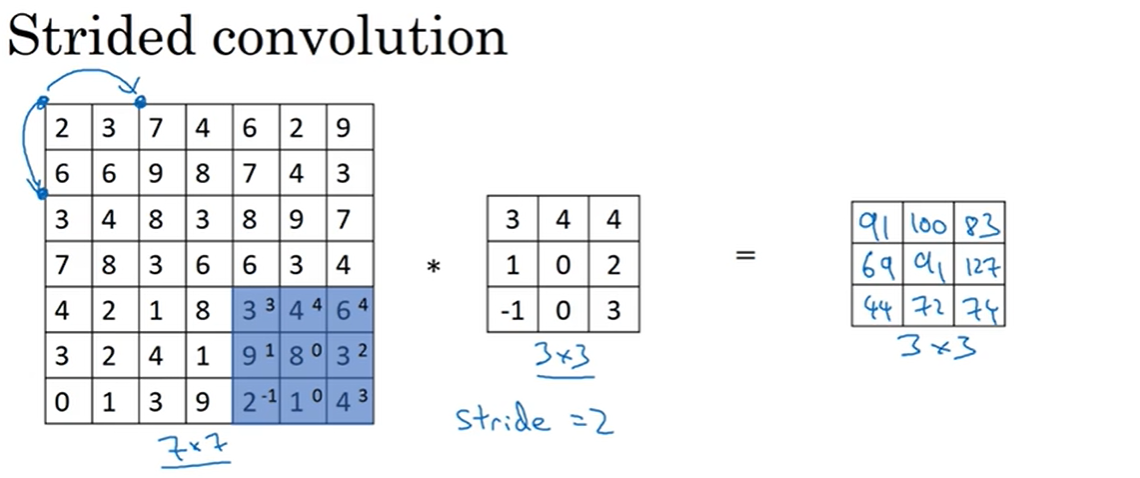
卷积步长是指卷积核每次移动的跨度。
如下图,步长为2,则卷积核每次移动2个格子。
-5.2 步长公式
计算公式
-5.3 卷积与交叉相关
在本文中的"卷积"并非实际意义上的卷积,技术层面来说,应该是交叉相关(cross-correlation),而不是卷积
在信号处理或者其他数学分支领域,对卷积核进行翻转,会使卷积核保持结合律:
(A * B) * C = A * (B * C)
这一性质在信号处理领域很有用,但在深度神经网络中它并不重要
所以元素间相乘简化了代码,而且这一改变之后,不影响使用
为了方便,大多数人叫这个卷积,即使有时数学家更喜欢叫它互相关
叫法在练习中写的代码没有影响,并且对阅读文献的能力没有影响
但是在深度学习文献中,由于约定,会把交叉相关的操作称之为"卷积"
总之,在机器学习的约定中,通常忽略掉’‘翻转’'操作
技术上,我们进行的操作最好称之为交叉相关
但是,大多数深度学习的文献都叫它卷积操作
在此处也延续此称呼为卷积
六、三维卷积(Convolution over volumes)
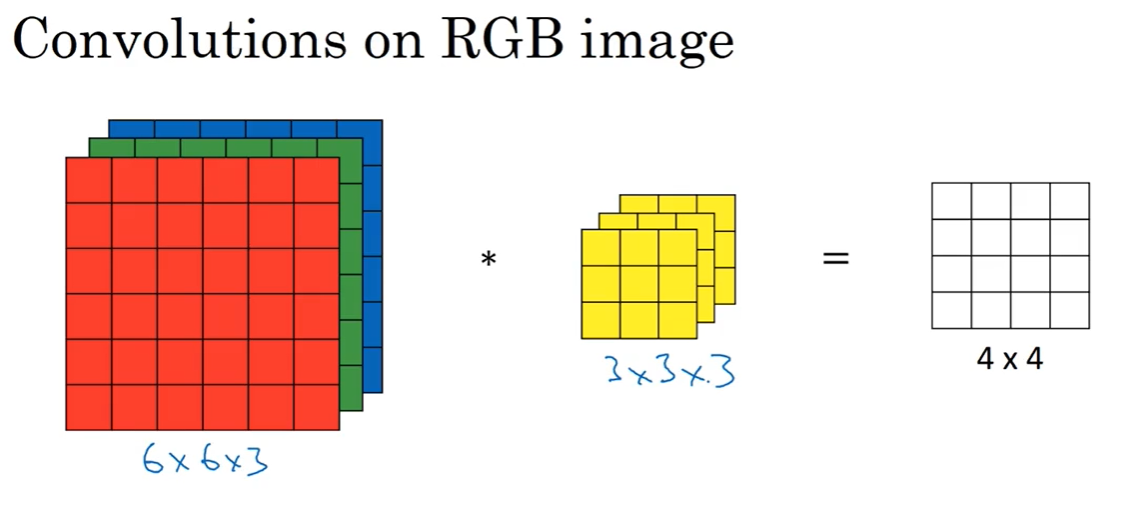
-6.1 单卷积核
6x6x3 * 3x3x3=4x4
计算时,27个数分别对应相乘,然后将27个数相加。最终得到4x4矩阵的每个元素
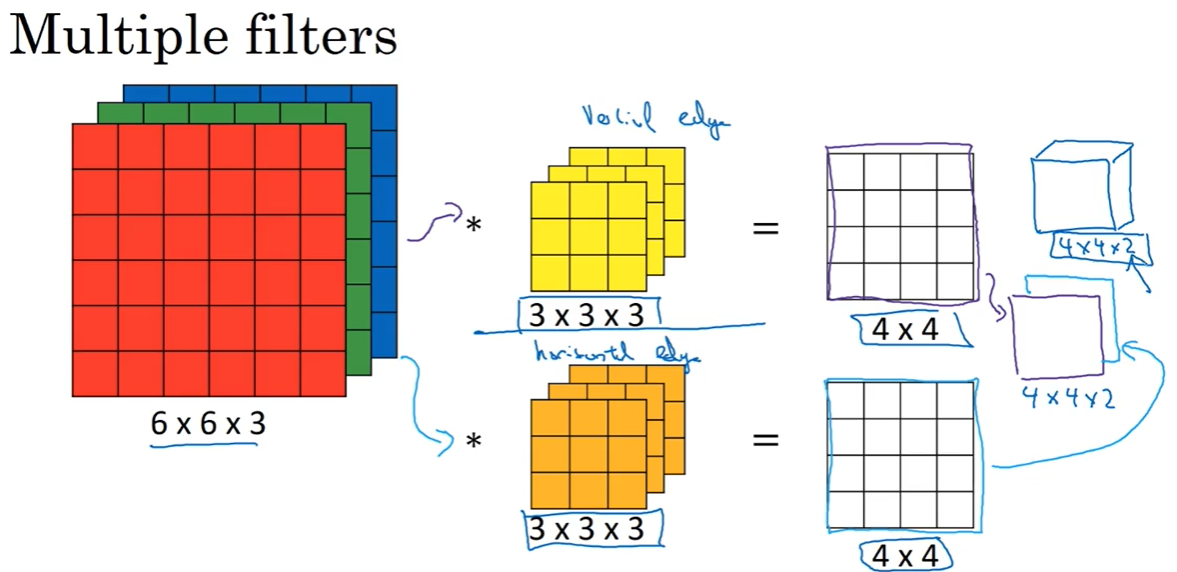
-6.2 多卷积核
如果想同时探测竖直方向的线和水平方向的线,那么可以
设计两个卷积核
-6.3 Summary
n x n x ncn_cnc image * f x f x ncn_cnc filter = n-f+1 x n-f+1 x nc′n_c^\\primenc′
ncn_cnc:通道数量,文献中被称为3D立方体的深度
nc′n_c^\\primenc′:使用过滤器数量