思维导图

二叉树的创建 

先定义一个二叉树链式结构的结构体

typedef int BTDatatype;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDatatype data;
}BTNode;

手搓一个二叉树（前序遍历的方式创建二叉树放到OJ题里）

BTNode* BuyNode(BTDatatype x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* CreateBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3); BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

二叉树的前序、中序、后序遍历

区别在于访问根节点的时机不同 

下面是遍历二叉树的递归流程图 

前序

void PreOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}

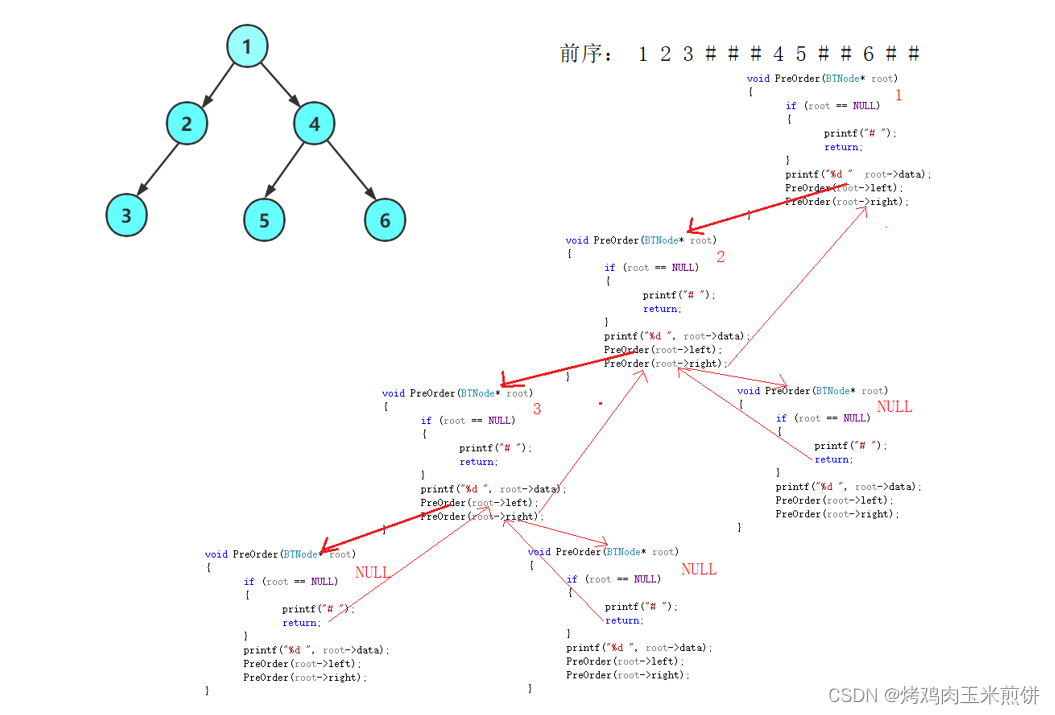中序

void InOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}

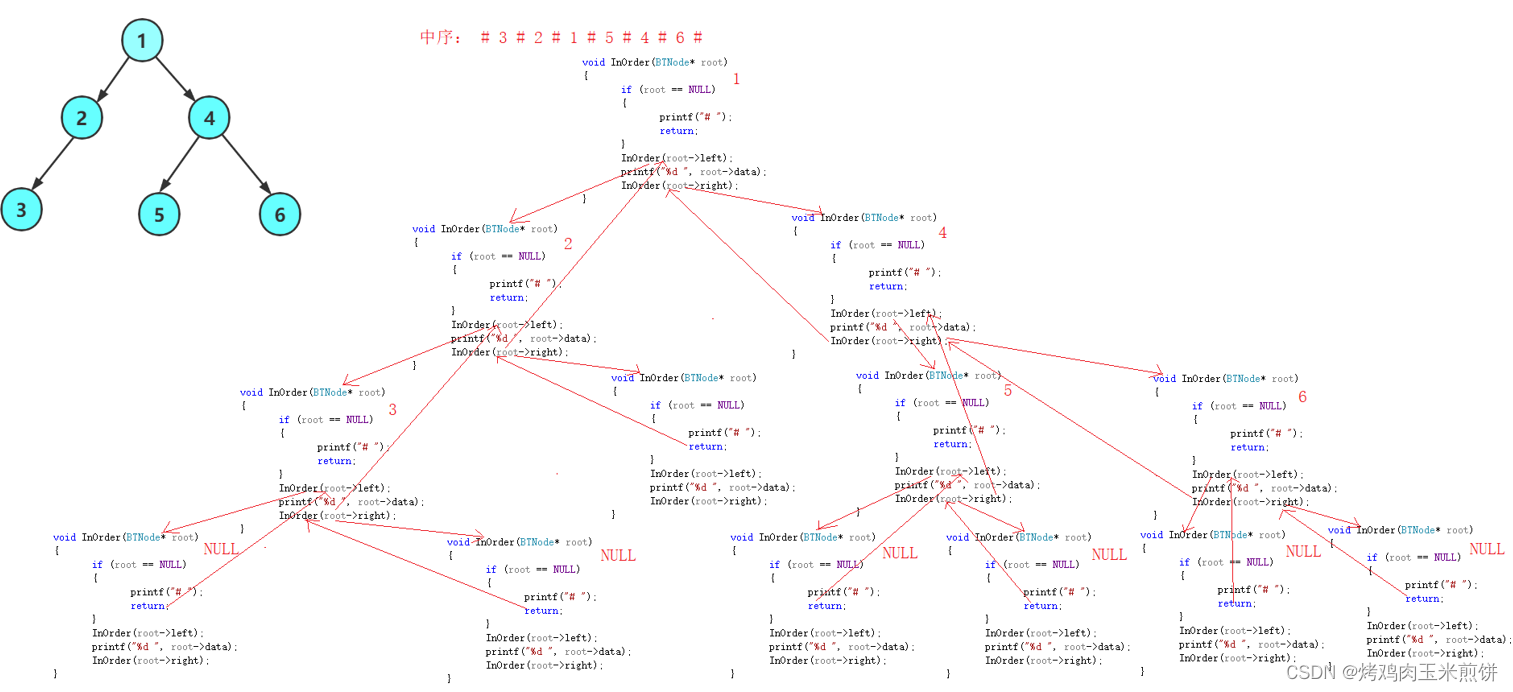后序 

void PostOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

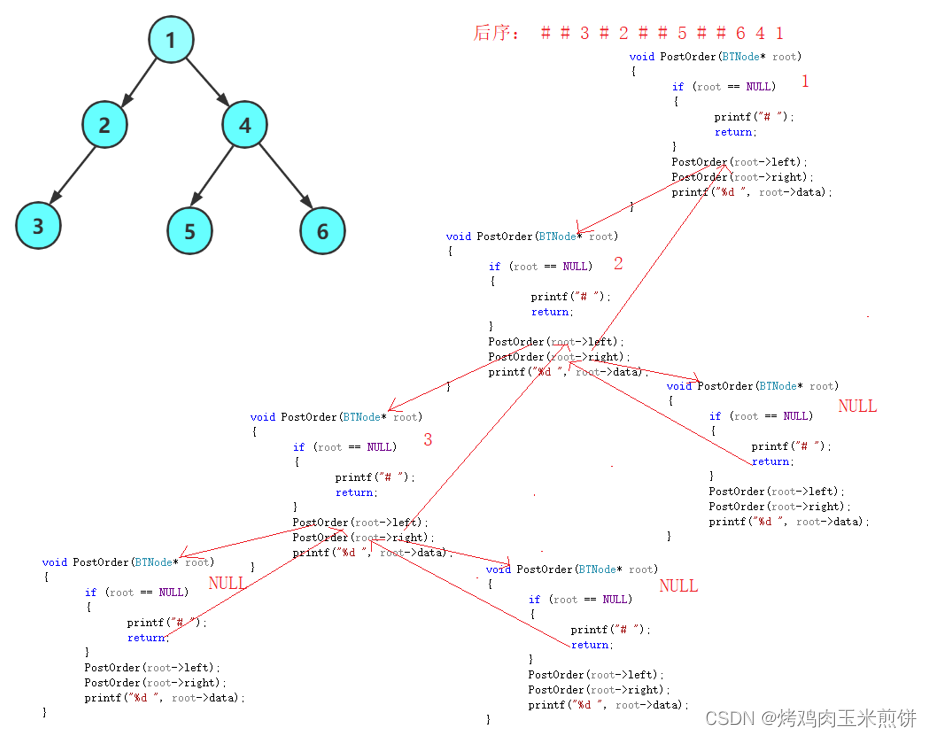
3个图的递归次序看上去差不多，每次函数结束之后都是回到调用它的地方。

二叉树的销毁 

采用后序遍历的方式比较简单 

void BinaryTreeDestroy(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);printf("free: %d\\n", root->data);free(root);
}

二叉树的层序遍历

需要先拥有一个队列，这里将之前写过的队列直接拿过来，值得注意的地方是要在队列的头文件里加一个前置声明（不然找不到二叉树的结构体），并改一下队列的数据类型

// 前置声明
struct BinatyTreeNode;typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;

其他函数

计算二叉树的节点

​
int BinaryTreeSize(BTNode* root)
{return root == NULL ?  0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}​

计算二叉树的叶子节点

int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

计算二叉树的深度

int maxDepth(struct TreeNode* root){if (root == NULL){return 0;}int left = maxDepth(root->left) + 1;int right = maxDepth(root->right) + 1;return left > right ? left : right;
}

计算二叉树的第k层的节点数量

int BinaryTreeKlevel(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeKlevel(root->left, k - 1) + BinaryTreeKlevel(root->right, k - 1);
}

查找二叉树的某个值

BTNode* BinaryTreeFind(BTNode* root, BTDatatype x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2)return ret2;return NULL;
}

判断是否为完全二叉树

利用层序的思路来写

int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){// 把空节点也入队列QueuePush(&q, front->left);QueuePush(&q, front->right);}else{// 出到空节点的时候跳出循环break;}}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){// 后面还有非空节点，则不是完全二叉树QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

一些OJ题目

1. 单值二叉树。

965. 单值二叉树 - 力扣（LeetCode）

思路：前序遍历二叉树，比较根、左子树、右子树的值是否相同
2. 检查两颗树是否相同。

100. 相同的树 - 力扣（LeetCode）

思路：分两个指针去前序遍历，先判断结构是否相同，再判断值是否相同
3. 对称二叉树。

101. 对称二叉树 - 力扣（LeetCode）

思路：利用第2题的思路，左子树按照根、左子树、右子树的次序遍历，右子树按照、根、右子树、左子树的次序遍历
4. 二叉树的前序遍历。 

144. 二叉树的前序遍历 - 力扣（LeetCode）

思路：注意每一次函数调用结束后当前的形参是会销毁的
5. 二叉树中序遍历 。

94. 二叉树的中序遍历 - 力扣（LeetCode）
6. 二叉树的后序遍历 。

145. 二叉树的后序遍历 - 力扣（LeetCode）
7. 另一颗树的子树。

572. 另一棵树的子树 - 力扣（LeetCode）

思路：每一个节点都看作是字树，然后用第2题的思路去依次比较

8.二叉树的构建及遍历

二叉树遍历_牛客题霸_牛客网 (nowcoder.com) 

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef char BTDatatype;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDatatype data;
}BTNode;BTNode* BuyNode(BTDatatype x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* CreateTree(char* str, int* pi)
{if (str[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BuyNode(str[(*pi)++]);root->left = CreateTree(str, pi);root->right = CreateTree(str, pi);return root;
}void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}int main()
{char a[100];scanf("%s", a);int i = 0;BTNode* preOrder = CreateTree(a, &i);InOrder(preOrder);return 0;
}

 也是利用前序遍历的思想，输入数组的下标传给构建函数的是指针。