一、计算机基础单位

• 位（比特）：b bit
• 字节：B byte
  • 1B=8b
• 千字节：KB
  • 1KB=1024B
• 兆字节：MB
  • 1MB=1024KB
• 吉字节：GB
  • 1GB=1024MB
• 太字节：TB
  • 1TB=1024GB
• 最小的数据单位：b
• 最小的存储单位：B

二、进制

1.进制表示符号

  十进制（D）；二进制（B）；八进制（O）；十六进制（H）。

• 十进制（0~9）：1、2、50、102；
• 二进制（0~1）：11001（二进制）=25（十进制）
• 八进制（0~7）：31（八进制）=25（十进制）
• 十六进制（0~F）：用A来表示10，B表示11，C表示12，D表示13，E表示14，F表示15
  • 19（十六进制）=25（十进制）

2.进制之间的转换：

(1)十进制转换为二进制（例子：173）

(2)十进制转换为八进制

  方法一：先将十进制转换为二进制，再转换为八进制。
  方法二：同十进制转换为二进制一样，将除2取余变为除8取余。
  如遇小数，则乘8取整法，即将小数部分乘以8，然后取整数部分，剩下的小数部分继续乘以8，然后取整数部分，剩下的小数部分又乘以8，一直取到小数部分为零为止。如果永远不能为零，就同十进制数的四舍五入一样3舍4入。

（3）十进制转换为十六进制

  方法一：先将十进制转换为二进制，再转换为十六进制。
  方法二：除十六取余。（同十转八）

（4）二进制转换为十进制

  无符号整数的二进制转化为十进制数，从二进制数的右边第一位起，从右往左，先用二制位置上的数乘以2的相应位数的幂，然后把每一位的乘积相加即可得到二进制数对应的十进制数。

  如果是带符号的二进制数转化为十进制数：先观察二进制数最高位是什么数，如果是1，则表示是负数，如果是0则表示是正数，确定符号后再来转化为十进制数。

  小数转化为十进制的方法：小数的二进制数转化为十进制数的方法，从左往右，用二进制位数上的数字乘以2的负位数次幂，然后把所有乘积相加即可得。

（5）二进制转换为八进制

  取三合一法，即从二进制的小数点为分界点，向左（或向右）每三位取成一位。

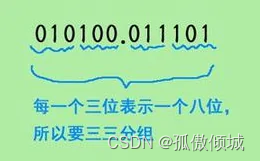
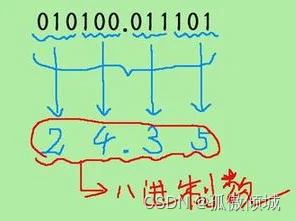
（6）二进制转换为十六进制

  二进制转16进制，只需将2进制数从右向左每四位一组合，每一个组合以一个十六进制数表示，(注意位数不足补0)。

3.进制的加减法

（1）加法（逢n进1）

  二进制：0+0=0；0+1=1；1+0=1；1+1=10；0进位为1。

  八进制：逢 8 进 1

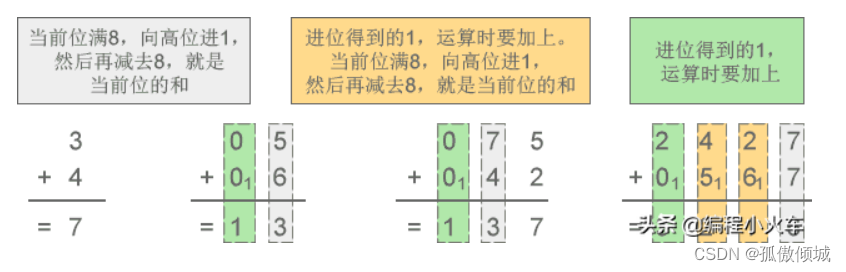
  十六进制：基数为16，加法运算时逢16进1。

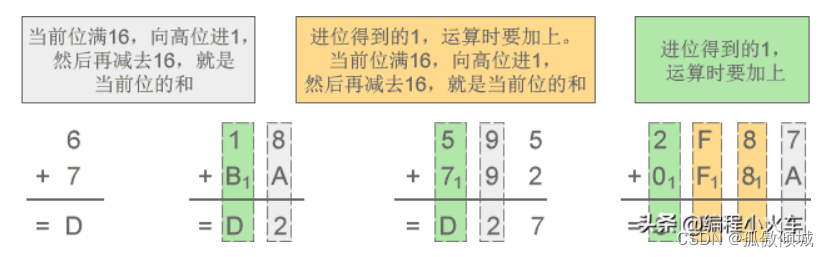
（2）减法：

  二进制：0－0=0，1－0=1，1－1=0，0－1=1。

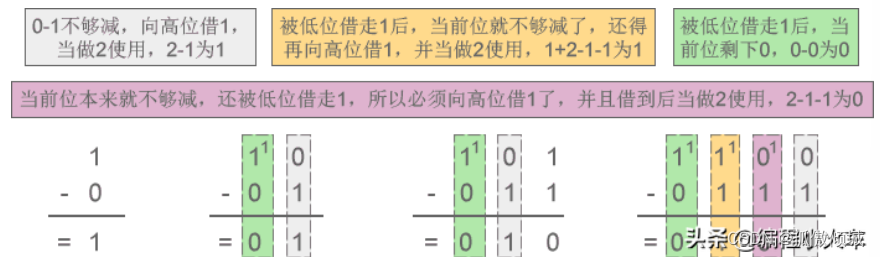
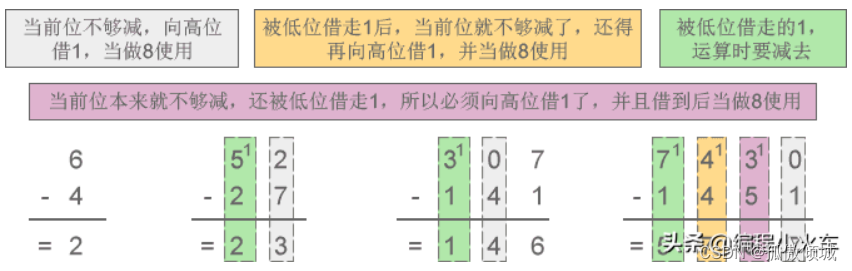
  八进制：借1当8

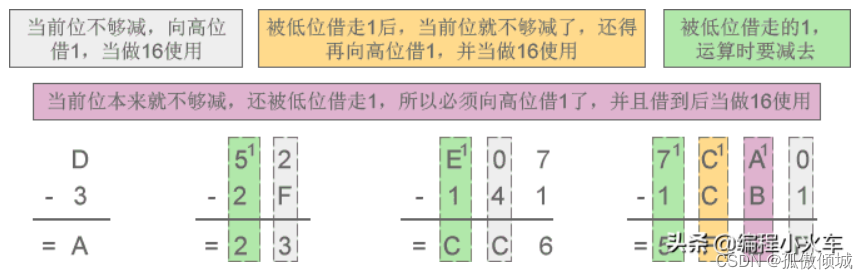
  十六进制：借1当16

三、例题一

  内存按字节编址从B3000H 到 DABFFH的区域其存储容量为_____。(2015年下半年)
  A. 123KB
  B.159KB
  C.163KB
  D.194KB

答案：B
解析：
  B3000H=733184D；
  DABFFH=895999D；
  存储容量为（895999-733184）/1024约等于159KB。

四、例题二

  内存按字节编址。若用存储容量为32K × 8bit的存储器芯片构成地址从A0000H到DFFFFH的内存，则至少需要____片芯片。(2017年下半年)
  A. 4
  B.8
  C.16
  D.32

答案：B
解析：
  A0000H=655360D；
  DFFFFH=917503D；
  内存为917503-655360=262143(单位：B)；
  262143B*8bit（该步骤作用为统一单位）；
  262143/1024=256k（再将B转换为K）；
  即所需芯片=256/32=8