二分查找算法最靠左索引最靠右索引详解与优化:图文全解+代码详注+思路分析

文章目录
- 1.二分查找算法初识
-
- 1.1 简介
- 1.2 实现思路
- 2.二分查找基础版-查找范围左闭右闭
-
- 2.1 需求分析
- 2.2 算法描述
- 2.3 代码实现
- 3.基础版的几个问题
-
- 3.1 循环条件不加 left == right 行不行
- 3.2 left + right 超过int最大值问题
- 4.二分查找改变版-查找范围左闭右开
- 5.衡量算法的好坏-时间复杂度
-
- 5.1 两种算法代码语句执行次数
-
- 🍀 二分查找
- 🍀 线性查找
- 5.2 代码执行次数图形化比较
- 5.3 大O表示法图形化比较
- 6.二分查找性能
-
- 6.1 时间复杂度
- 6.2 空间复杂度
- 7.二分查找平衡版
- 8.Java源码中二分查找的使用
-
- 8.1 Arrays.binarySearch(int[] a, int key)
- 8.2 实现二分查找目标值,不存在则插入
- 9.LeftRightmost
-
- 9.1 最靠左索引
- 9.2 最靠右索引
- 9.3 返回≥目标的最靠左索引
-
- 🍀 普通代码
- 🍀 第一次优化
- 🍀 第二次优化
- 9.4 返回≤目标的最靠右索引
-
- 🍀 普通代码
- 🍀 第一次优化
- 🍀 第二次优化
- 9.5 实际应用
1.二分查找算法初识
1.1 简介
二分查找算法,也称折半查找算法,是一种在有序数组中查找某一特定元素的搜索算法。
1.2 实现思路
- 初始状态下,将整个序列作为搜索区域;
- 找到搜索区域内的中间元素,和目标元素进行比对;
- 如果相等,则搜索成功;
- 如果中间元素大于目标元素,表明目标元素位于中间元素的左侧,将左侧区域作为新的搜素区域;
- 反之,若中间元素小于目标元素,表明目标元素位于中间元素的右侧,将右侧区域作为新的搜素区域;
- 重复执行第二步,直至找到目标元素。如果搜索区域无法再缩小,且区域内不包含任何元素,则表明整个序列中没有目标元素,查找失败。
2.二分查找基础版-查找范围左闭右闭
2.1 需求分析
需求:在有序数组 AAA 内,查找值 targetValuetargetValuetargetValue
- 如果找到返回索引
- 如果找不到返回 −1-1−1
2.2 算法描述
| 算法描述 | |
|---|---|
| 前提 | 给定一个内含 nnn 个元素的有序数组 AAA,满足 A0≤A1≤A2≤⋯≤An−1A_{0}\\leq A_{1}\\leq A_{2}\\leq \\cdots \\leq A_{n-1}A0≤A1≤A2≤⋯≤An−1,一个待查值 targetValuetargetValuetargetValue |
| 1 | 设置 left=0left=0left=0,right=n−1right=n-1right=n−1 |
| 2 | 如果 left>rightleft \\gt rightleft>right,结束查找,没找到 |
| 3 | 设置 mid=floor(left+right2)mid = floor(\\frac {left + right}{2})mid=floor(2left+right) ,midmidmid 为中间索引,floorfloorfloor 是向下取整(≤left+right2\\leq \\frac {left+right}{2}≤2left+right 的最小整数) |
| 4 | 如果 targetValue<AmtargetValue < A_{m}targetValue<Am 设置 right=mid−1right = mid - 1right=mid−1,跳到第2步 |
| 5 | 如果 Amid<targetValueA_{mid} < targetValueAmid<targetValue 设置 left=mid+1left = mid + 1left=mid+1,跳到第2步 |
| 6 | 如果 Am=targetValueA_{m} = targetValueAm=targetValue,结束查找,找到了 |
2.3 代码实现
/* 二分查找基础版 @param array 待查找的升序数组* @param targetValue 待查找的目标值* @return 找到则返回目标值的索引,找不到返回-1*/public static int binarySearchBasic(int[] array, int targetValue) {// 设置指针 left 指向数组的开始索引位置int left = 0;// 设置指针 right 指向数组的最后索引位置int right = array.length - 1;// 定一个 mid,表示 left 和 right 的中间索引位置int mid;/*对 [left,right] 范围内的元素进行查找,left <= right 成立说明在 [left,right] 范围内还有元素可以可以查找while循环退出的两种方式:- 进入了 else,说明找到了,返回中间索引- 不满足 left <= right,说明范围不断缩小后依旧没有找到,退出循环*/while (left <= right) {// 查找中间索引,如果 (left+right)/2 为小数则会自动向下取整mid = (left + right) / 2;if (targetValue < array[mid]) {// 如果 目标值 小于 中间索引值,说明 目标值索引 应该在 中间索引 的左边// 我们可以通过调整 right 的值缩小查找范围right = mid - 1;} else if (array[mid] < targetValue) {// 如果 目标值 大于 中间索引值,说明 目标值索引 应该在 中间索引 的右边// 我们可以通过调整 left 的值缩小查找范围left = mid + 1;} else {// 否则说明 目标值 等于 中间索引值,也就说明我们找到了return mid;}}// 走到这里说明没有进入过上面 while 中的else,while循环退出时 left > right// 说明没有找到return -1;}
3.基础版的几个问题
3.1 循环条件不加 left == right 行不行
不行,因为这意味着当 left 和 right 相等时,会漏掉 left 和 right 共同指向的元素会漏过与目标值的比较。
3.2 left + right 超过int最大值问题
我们先来举个模拟例子:
public static void main(String[] args) {// 模拟 二分查找中的 leftint left = 100;// 模拟 二分查找中的 rightint right = Integer.MAX_VALUE - 1;// 此时 left+right 的值超过了 int范围 的最大值,导致 left + right 的结果为负数// 然后对负数进行除以2操作,结果依旧为负数int mid = (left + right) / 2;// 输出结果为 -1073741775System.out.println(mid);}
那如何解决这个问题呢?我们可以使用 位运算 来代替 /2 的操作。
算数右移
>>:低位溢出,符号位不变,并用符号位补溢出的高位。逻辑右击(无符号右移)
>>>:低位溢出,高位补0。由于最高位符号位为0表示该数为正数,因此相比于
>>做到了能将一个 负数 无符号右移后变成 正数。
/* 二分查找增强版 @param array 待查找的升序数组* @param targetValue 待查找的目标值* @return 找到则返回目标值的索引,找不到返回-1*/public static int binarySearchPlus(int[] array, int targetValue) {int left = 0;int right = array.length - 1;int mid;while (left <= right) {/*考虑到 left+right 的值可能会超过 int可表示 的最大值,我们不再对他们的和直接除以2我们知道 除以2 的操作可以用 位运算 >>1 来代替但还不够,由于 (left+right) 值溢出表示负数,>>1 只是做 除以2 操作,最高位符号位不变,依旧为1表示负数,负数除以2依旧是负数这时候我们可以修改为 无符号右移 >>>1 ,低位溢出,高位补0,那么最高位符号位为0就表示正数了*/mid = (left + right) >>> 1;if (targetValue < array[mid]) {right = mid - 1;} else if (array[mid] < targetValue) {left = mid + 1;} else {return mid;}}return -1;}
4.二分查找改变版-查找范围左闭右开
right 只是作为一个边界,指向的一定不是查找目标。
/* 二分查找改变版 @param array 待查找的升序数组* @param targetValue 待查找的目标值* @return 找到则返回目标值的索引,找不到返回-1*/public static int binarySearchPlus(int[] array, int targetValue) {// 设置指针 left 指向数组的开始索引位置int left = 0;// 设置指针 right 指向查找范围的后一个索引位置// 在这里 right 只是作为一个边界,指向的一定不是查找目标。int right = array.length;int mid;// 在 [left,right) 左闭右开的区间范围内进行目标值查找// 因为 right 只是一个边界不作为查找索引,因此不能将 left <= right 作为条件while (left < right) {mid = (left + right) >>> 1;if (targetValue < array[mid]) {// 目标值 小于 中间索引值,则应该将右范围缩小// 需要将查找范围变为 [left,mid)right = mid;} else if (array[mid] < targetValue) {left = mid + 1;} else {return mid;}}return -1;}
5.衡量算法的好坏-时间复杂度
5.1 两种算法代码语句执行次数
🍀 二分查找
public static int binarySearchBasic(int[] a, int target) {// 设置指针和初值int i = 0;int j = a.length - 1;// L 次 元素在最左边 L 次, 元素在最右边 2*L 次while (i <= j) {// i~j 范围内有东西int m = (i + j) >>> 1;if (target < a[m]) {// 目标在左边j = m - 1;} else if (a[m] < target) {// 目标在右边i = m + 1;} else {// 找到了return m;}}return -1;}/*1 [2,3,4,5] 5 右侧没找到更差int i = 0, j = a.length - 1; 2return -1; 1元素个数 循环次数4-7 3 floor(log_2(4)) = 2+18-15 4 floor(log_2(8)) = 3+116-31 5 floor(log_2(16)) = 4+132-63 6 floor(log_2(32)) = 5+1... ...循环次数L = floor(log_2(n)) + 1i <= j L+1int m = (i + j) >>> 1; Ltarget < a[m] La[m] < target Li = m + 1; L代码执行次数公式:(floor(log_2(n)) + 1) * 5 + 4当n=4时,(3) * 5 + 4 = 19*t当n=1024时,(10 + 1) * 5 + 4 = 59*t*/
🍀 线性查找
/* <h3>线性查找</h3> @param a 待查找的升序数组 (可以不是有序数组)* @param target 待查找的目标值* @return <p>找到则返回索引</p>* <p>找不到返回 -1</p>*/public static int linearSearch(int[] a, int target) {for (int i = 0; i < a.length; i++) {if (a[i] == target) {return i;}}return -1;}// 1. 最差的执行情况// 2. 假设每行语句执行时间一样 t/*数据元素个数 nint i = 0; 1i < a.length; n+1i++ na[i] == target nreturn -1; 1算法运行语句总次数:3*n + 3当n=4时,3*4 + 3 = 15*t当n=1024时,3*1024 + 3 = 3075*t*/
5.2 代码执行次数图形化比较
采用 Desmos | 图形计算器 工具对两种算法的代码执行次数进行比较。
- x 轴表示数组的数据量大小。
- y 轴表示代码语句执行次数。
二分查找算法执行次数公式:3⋅x+33\\cdot x+33⋅x+3
线性查找算法执行次数公式:(floor(log2(x))+1)⋅5+4\\left(\\operatorname{floor}\\left(\\log_{2}\\left(x\\right)\\right)+1\\right)\\cdot5+4(floor(log2(x))+1)⋅5+4
当数组数据量比较小,即 x 值比较小的时候,执行次数比较为:
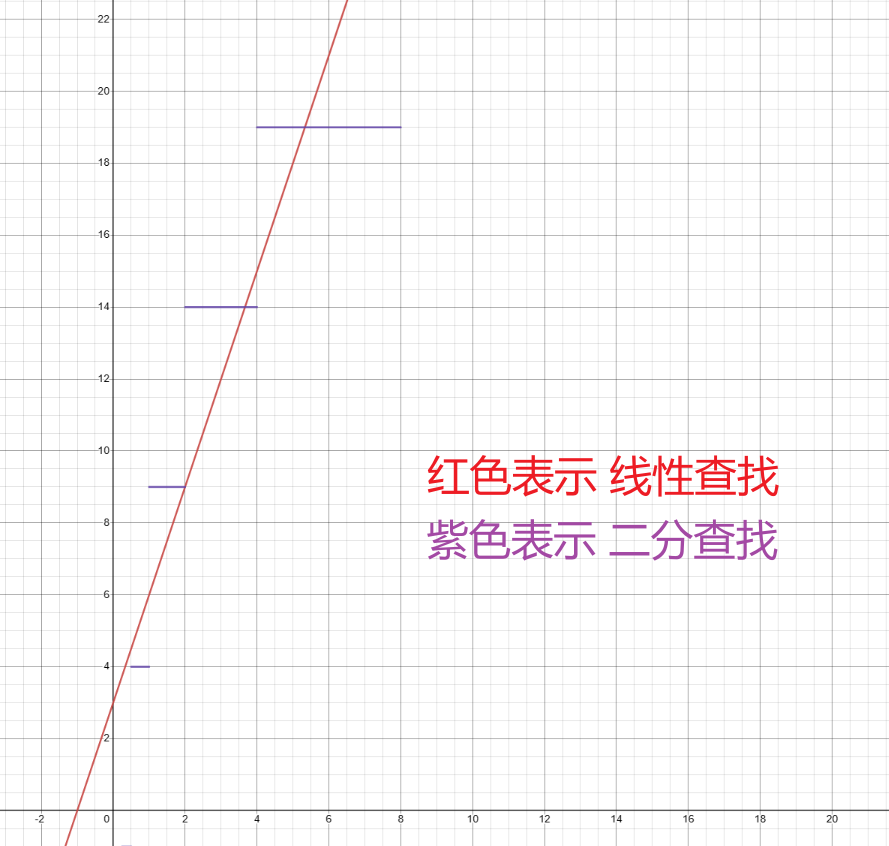
当数组数据量比较大,即 x 值比较大的时候,执行次数比较为:
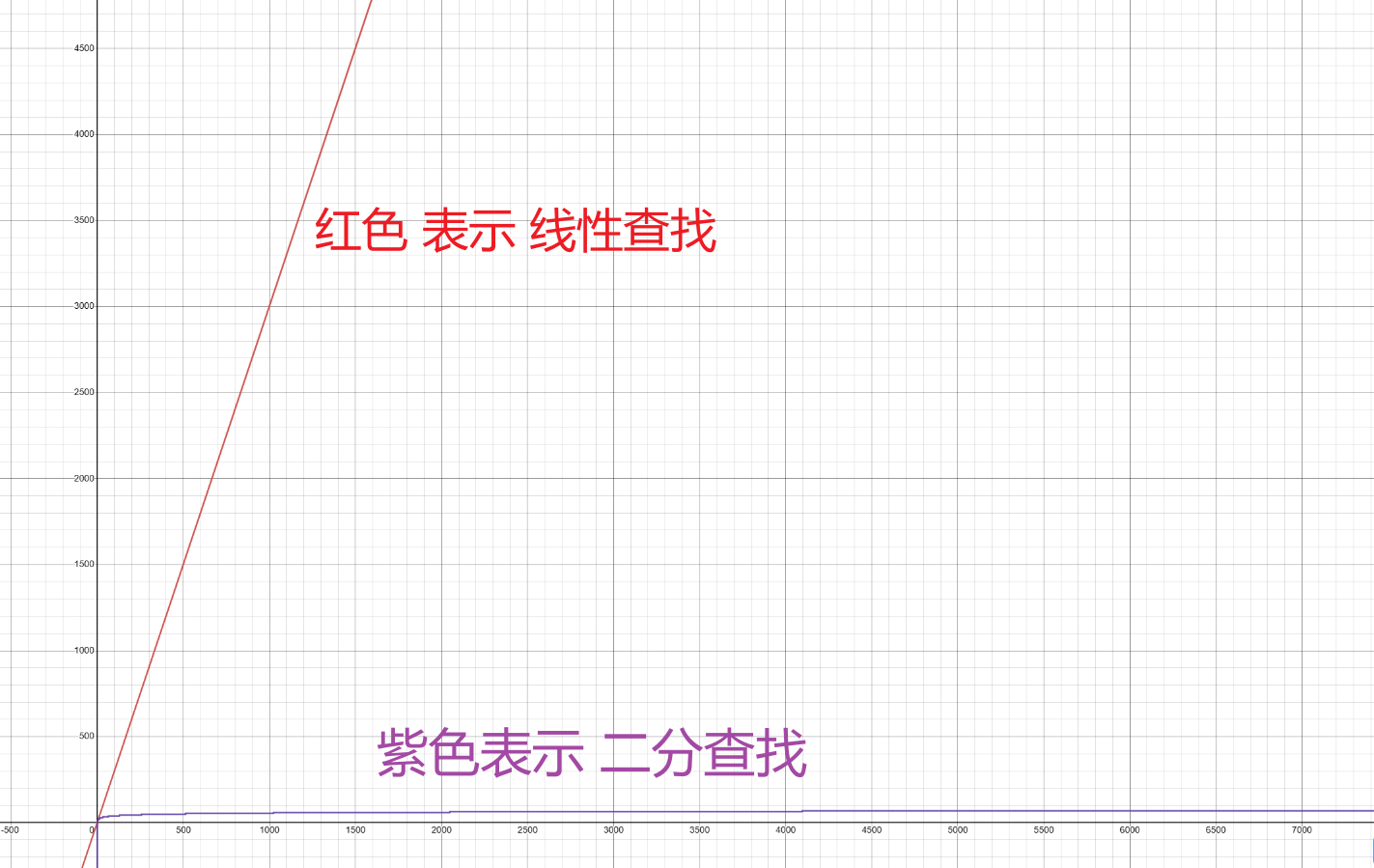
5.3 大O表示法图形化比较
二分查找算法:O(log(n))O(log(n))O(log(n))
线性查找算法:O(n)O(n)O(n)

6.二分查找性能
6.1 时间复杂度
- 最坏情况:O(logn)O(log n)O(log n)
- 最好情况:如果待查找元素恰好在数组中央,只需要循环一次 O(1)O(1)O(1)
6.2 空间复杂度
- 需要常数个指针 left,right, mid,因此额外占用的空间是 O(1)O(1)O(1)
7.二分查找平衡版
/* <h3>二分查找平衡版</h3> <ol>* <li>不奢望循环内通过 m 找出目标, 缩小区间直至剩 1 个, 剩下的这个可能就是要找的(通过 i)</li>* <li>i 指针可能是查找目标</li>* <li>j 指针不可能是查找目标</li>* <li>因为 1. 2. 3. 当区域内还剩一个元素时, 表示为 j - i == 1</li>* <li>改变 i 边界时, m 可能就是目标, 同时因为 2. 所以有 i=m</li>* <li>改变 j 边界时, m 已经比较过不是目标, 同时因为 3. 所以有 j=m</li>* <li>三分支改为二分支, 循环内比较次数减少</li>* </ol> @param a 待查找的升序数组* @param target 待查找的目标值* @return <p>找到则返回索引</p>* <p>找不到返回 -1</p>*/public static int binarySearchBalance(int[] a, int target) {int i = 0, j = a.length;while (1 < j - i) { // 范围内待查找的元素个数 > 1 时int m = (i + j) >>> 1;if (target < a[m]) { // 目标在左边j = m;} else { // 目标在 m 或右边i = m;}}return (target == a[i]) ? i : -1;}
思想:
- 左闭右开的区间,i 向的可能是目标,而 j 指向的不是目标
- 不奢望循环内通过 m 找出目标, 缩小区间直至剩 1 个, 剩下的这个可能就是要找的(通过 i)
- j − i > 1 的含义是,在范围内待比较的元素个数 > 1
- 改变 i 边界时,它指向的可能是目标,因此不能 m + 1
- 循环内的平均比较次数减少了
- 时间复杂度 Θ(log(n))Θ(log(n))Θ(log(n)) (最坏最好情况)
8.Java源码中二分查找的使用
8.1 Arrays.binarySearch(int[] a, int key)
/* 使用二进制搜索算法在指定的整数数组中搜索指定的值。在进行此调用之前,必须对数组进行排序(按方法排序 sort(int[]) )。* 如果未排序,则结果未定义。如果数组包含多个具有指定值的元素,则无法保证会找到哪个元素。* 参数:* a – 要搜索的数组 * key – 要搜索的值* 返回:搜索键的索引(如果它包含在数组中);否则,( -(插入点)-1)。* 插入点定义为将键插入数组的 点 :第一个元素的索引大于键,如果数组中的所有元素都小于指定的键,则为 a.length 。* 请注意,这保证了当且仅当找到键时返回值将为 >= 0。*/public static int binarySearch(int[] a, int key) {return binarySearch0(a, 0, a.length, key);}// Like public version, but without range checks.private static int binarySearch0(int[] a, int fromIndex, int toIndex,int key) {int low = fromIndex;int high = toIndex - 1;while (low <= high) {int mid = (low + high) >>> 1;int midVal = a[mid];if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}return -(low + 1); // key not found.}
8.2 实现二分查找目标值,不存在则插入
public static void main(String[] args) {// 二分查找目标值,不存在则插入/*原始数组:[2,5,8]查找目标值:4查询不到,返回的结果为 r = -待插入点索引-1在这里带插入点索引为 1,对应 r = -2那么我们分成这几步来进行拷贝:- 1.新建数组,大小为原数组的大小+1: [0,0,0,0]- 2.将待插入点索引之前的数据放入新数组: [2,0,0,0]- 3.将目标值放入到待插入点索引的位置: [2,4,0,0]- 4.将原数组后面的数据都相继拷贝到新数组后面: [2,4,5,8]*/// 定义原数组与目标值int[] oldArray = {2, 5, 8};int target = 4;// 搜索目标值4,没有找到,返回结果为 r = -待插入点索引-1,这里的 r=-2int r = Arrays.binarySearch(oldArray, target);// r < 0 说明没有找到目标值,就插入if (r < 0) {// 获取待插入索引int insertIndex = -r - 1;// 1.新建数组,大小为原数组的大小+1int[] newArray = new int[oldArray.length + 1];// 2.将待插入点索引之前的数据放入新数组System.arraycopy(oldArray, 0, newArray, 0, insertIndex);// 3.将目标值放入到待插入点索引的位置newArray[insertIndex] = target;// 4.将原数组后面的数据都相继拷贝到新数组后面System.arraycopy(oldArray, insertIndex, newArray, insertIndex + 1, oldArray.length - insertIndex);System.out.println(Arrays.toString(newArray));}}
9.LeftRightmost
9.1 最靠左索引
搜索目标值为 target 且 索引最小的索引位置
public static int binarySearchLeftmost(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;// 记录最小索引int minIndex = -1;while (left <= right) {mid = (left + right) >>> 1;if (target < array[mid]) {// 目标值小于中间索引值,缩小右范围right = mid - 1;} else if (array[mid] < target) {// 目标值大于中间索引值,缩小左范围left = mid + 1;} else {minIndex = mid;// 由于要查找最小索引,因此缩小右范围即可right = mid - 1;}}// 返回结果return minIndex;}
9.2 最靠右索引
搜索目标值为 target 且 索引最大的索引位置
public static int binarySearchRightmost(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;// 记录最大索引int maxIndex = -1;while (left <= right) {mid = (left + right) >>> 1;if (target < array[mid]) {// 目标值小于中间索引值,缩小右范围right = mid - 1;} else if (array[mid] < target) {// 目标值大于中间索引值,缩小左范围left = mid + 1;} else {maxIndex = mid;// 由于要查找最大索引,因此缩小左范围即可left = mid + 1;}}// 返回结果return maxIndex;}
9.3 返回≥目标的最靠左索引
搜索大于等于目标值的最小索引位置
🍀 普通代码
public static int binarySearchLeftmostFirst(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;// 记录最小索引int minIndex = -1;while (left <= right) {mid = (left + right) >>> 1;if (target < array[mid]) {// array[mid] 满足大于目标值,因此可以记录minIndex = mid;// 目标值小于中间索引值,缩小右范围right = mid - 1;} else if (array[mid] < target) {// 目标值大于中间索引值,缩小左范围left = mid + 1;} else {// array[mid] 满足等于目标值,因此可以记录minIndex = mid;// 由于要查找最小索引,因此缩小右范围即可right = mid - 1;}}// 返回结果,如果返回为-1说明没有找到,即数组所有元素都比目标值要小return minIndex;}
🍀 第一次优化
可以看到 while 循环中的 if 和 else if 中的语句相同,因此可以做一次合并。
在 if 语句中,我们的操作是:
- 找到了 mid 索引,满足 array[mid] 大于等于目标值,
- 用 minIndex 记录这个大于等于目标值的索引,
- 然后将 mid -1 赋值给 right,也就是 (right + 1) 为 当前找到的 大于等于目标值的最小索引。
if 语句结束,就可以继续向前搜索看是否比当前 minIndex 更小的大于等于目标值的索引。
在本次优化中,我们保证了:
- 除非目标值大于数组元素的最大值,
- 否则最终循环结束时的 (right + 1) 指针指向的一定是大于等于目标值的最小索引,
- 也就是 minIndex = right + 1 。
public static int binarySearchLeftmostSecond(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;// 记录最小索引int minIndex = -1;/*在 if 语句中,我们的操作是:1. 找到了 mid 索引,满足 array[mid] 大于等于目标值,2. 用 minIndex 记录这个大于等于目标值的索引,3. 然后将 mid -1 赋值给 right,也就是 (right + 1) 为当前找到的大于等于目标值的最小索引。if语句结束,就可以继续向前搜索看是否比当前 minIndex 更小的大于等于目标值的索引。在本次优化中,我们保证了:除非目标值大于数组元素的最大值,否则最终循环结束时的 (right + 1) 指针指向的一定是大于等于目标值的最小索引,也就是 minIndex = right + 1 。这个结论是后面的第二次优化的核心!!!*/while (left <= right) {mid = (left + right) >>> 1;if (target <= array[mid]) {// array[mid] 满足大于等于目标值,因此可以记录minIndex = mid;// 目标值小于中间索引值,缩小右范围right = mid - 1;} else if (array[mid] < target) {// 目标值大于中间索引值,缩小左范围left = mid + 1;}}// 返回结果return minIndex;}
🍀 第二次优化
在第一次优化中,我们保证了:
- 除非目标值大于数组元素的最大值,
- 否则最终循环结束时的 (right + 1) 指针指向的一定是大于等于目标值的最小索引,
- 也就是最终 minIndex = right + 1 。
我们再肯定一件事情:最终退出while循环的情况一定是 left > right 且 right + 1 = left 。
而造成 left 比 right 多1,即 left 在 right 指针后面一位,一定是因为:
- 在以 left == right 为满足循环条件时,执行了 if 语句中right左移font> 或者 else if语句中的left右移。
- 我们之前又得到结论:最终循环结束时的 (right + 1) 指针指向的一定是大于等于目标值的最小索引。
- 当执行的是 if语句中的right左移后,导致了新(right + 1)的值就是left,则left就是大于等于目标值的最小索引。
- 当执行的是 else if语句中的left右移后,导致了left移动到了当前(right+1)指针的位置,则left就是大于等于目标值的最小索引。
综上所述,我们发现:
- 最终的left 指针就是那个大于等于目标值的最小索引,
- 所以我们无需用 minIndex 进行记录,直接最终 return left 即可。
- 那么这时候当目标值大于数组元素的最大值时,返回的left 就是 数组最大索引+1。
public static int binarySearchLeftmostThird(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;/*在第一次优化中,我们保证了:除非目标值大于数组元素的最大值,否则最终循环结束时的 (right + 1) 指针指向的一定是大于等于目标值的最小索引,也就是最终 minIndex = right + 1 。while (left <= right) {mid = (left + right) >>> 1;if (target <= array[mid]) {minIndex = mid;right = mid - 1;} else if (array[mid] < target) {left = mid + 1;}}我们再肯定一件事情:最终退出while循环的情况一定是 left > right 且 right + 1 = left 。而造成 left 比 right 多1,即 left 在 right 指针后面一位,一定是因为在以 left == right 为满足循环条件时,执行了if 语句中right左移 或者 else if语句中的left右移。我们之前又得到结论:最终循环结束时的 (right + 1) 指针指向的一定是大于等于目标值的最小索引。- 当执行的是if语句中的right左移后,导致了新(right + 1)的值就是left,则left就是大于等于目标值的最小索引。- 当执行的是else if语句中的left右移后,导致了left移动到了当前(right+1)指针的位置,则left就是大于等于目标值的最小索引。综上所述,我们发现:最终的left 指针就是那个大于等于目标值的最小索引,所以我们无需用 minIndex 进行记录,直接最终 return left 即可。那么这时候当目标值大于数组元素的最大值时,返回的left 就是 数组最大索引+1。*/// 不需记录最小索引// int minIndex = -1;while (left <= right) {mid = (left + right) >>> 1;if (target <= array[mid]) {// array[mid] 满足大于等于目标值,因此可以记录// minIndex = mid;// 目标值小于中间索引值,缩小右范围right = mid - 1;} else if (array[mid] < target) {// 目标值大于中间索引值,缩小左范围left = mid + 1;}}// 返回结果return left;}
9.4 返回≤目标的最靠右索引
搜索小于等于目标值的最大索引位置
🍀 普通代码
public static int binarySearchRightmostFirst(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;// 记录最小索引int minIndex = -1;while (left <= right) {mid = (left + right) >>> 1;if (target < array[mid]) {// 目标值小于中间索引值,缩小右范围right = mid - 1;} else if (array[mid] < target) {// array[mid] 满足小于目标值,因此可以记录minIndex = mid;// 目标值大于中间索引值,缩小左范围left = mid + 1;} else {// array[mid] 满足等于目标值,因此可以记录minIndex = mid;// 由于要查找最大索引,因此缩小左范围即可left = mid - 1;}}
🍀 第一次优化
public static int binarySearchRightmostSecond(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;// 记录最大索引int maxIndex = -1;/*在 else if 语句中,我们的操作是:1. 找到了 mid 索引,满足 array[mid] 小于等于目标值,2. 用 maxIndex 记录这个小于等于目标值的索引,3. 然后将 mid + 1 赋值给 left,也就是 (left - 1) 为当前找到的小于等于目标值的最大索引。else if语句结束,就可以继续向后搜索看是否比当前 maxIndex 更大的小于等于目标值的索引。在本次优化中,我们保证了:除非目标值小于数组元素的最小值,否则最终循环结束时的 (left - 1) 指针指向的一定是小于等于目标值的最大索引,也就是 maxIndex = left - 1 。这个结论是后面的第二次优化的核心!!!*/while (left <= right) {mid = (left + right) >>> 1;if (target < array[mid]) {// 目标值小于中间索引值,缩小右范围right = mid - 1;} else if (array[mid] <= target) {// array[mid] 满足小于等于目标值,因此可以记录maxIndex = mid;// 目标值大于中间索引值,缩小左范围left = mid + 1;}}// 返回结果return maxIndex;}
🍀 第二次优化
public static int binarySearchRightmostThird(int[] array, int target) {int left = 0;int right = array.length - 1;int mid;/*在第一次优化中,我们保证了:除非目标值小于数组元素的最小值,否则最终循环结束时的 (left - 1) 指针指向的一定是小于等于目标值的最大索引,也就是最终 maxIndex = left - 1 。while (left <= right) {mid = (left + right) >>> 1;if (target < array[mid]) {right = mid - 1;} else if (array[mid] <= target) {maxIndex = mid;left = mid + 1;}}我们再肯定一件事情:最终退出while循环的情况一定是 left > right 且 right = left - 1。而造成 right 比 left 少1,即 right 在 left 指针前面一位,一定是因为在以 left == right 为满足循环条件时,执行了if 语句中right左移 或者 else if语句中的left右移。我们之前又得到结论:最终循环结束时的 (left - 1) 指针指向的一定是小于等于目标值的最大索引。- 当执行的是if语句中的right左移后,导致了right移动到了当前(left - 1)的指针位置,则right就是小于等于目标值的最大索引。- 当执行的是else if语句中的left右移后,导致了新(left-1)指针的位置就是当前right的位置,则right就是小于等于目标值的最大索引。综上所述,我们发现:最终的 right 指针就是那个小于等于目标值的最大索引,所以我们无需用 maxIndex 进行记录,直接最终 return right 即可。那么这时候当目标值小于数组元素的最小值时,返回的 right 就是 -1。*/// 不需记录最小索引// int maxIndex = -1;while (left <= right) {mid = (left + right) >>> 1;if (target < array[mid]) {right = mid - 1;} else if (array[mid] <= target) {
// maxIndex = mid;left = mid + 1;}}// 返回结果,当然这个结果也可以写成 return left - 1return right;}
9.5 实际应用

范围查询:
- 查询 x<4x \\lt 4x<4,0..leftmost(4)−10 .. leftmost(4) - 10..leftmost(4)−1
- 查询 x≤4x \\leq 4x≤4,0..rightmost(4)0 .. rightmost(4)0..rightmost(4)
- 查询 4<x4 \\lt x4<x,$rightmost(4) + 1 … \\infty $
- 查询 4≤x4 \\leq x4≤x, leftmost(4)..∞leftmost(4) .. \\inftyleftmost(4)..∞
- 查询 4≤x≤74 \\leq x \\leq 74≤x≤7,leftmost(4)..rightmost(7)leftmost(4) .. rightmost(7)leftmost(4)..rightmost(7)
- 查询 4<x<74 \\lt x \\lt 74<x<7,rightmost(4)+1..leftmost(7)−1rightmost(4)+1 .. leftmost(7)-1rightmost(4)+1..leftmost(7)−1
求排名:leftmost(target)+1leftmost(target) + 1leftmost(target)+1
- targettargettarget 可以不存在,如:leftmost(5)+1=6leftmost(5)+1 = 6leftmost(5)+1=6
- targettargettarget 也可以存在,如:leftmost(4)+1=3leftmost(4)+1 = 3leftmost(4)+1=3
求前任(predecessor):leftmost(target)−1leftmost(target) - 1leftmost(target)−1
- leftmost(3)−1=1leftmost(3) - 1 = 1leftmost(3)−1=1,前任 a1=2a_1 = 2a1=2
- leftmost(4)−1=1leftmost(4) - 1 = 1leftmost(4)−1=1,前任 a1=2a_1 = 2a1=2
求后任(successor):rightmost(target)+1rightmost(target)+1rightmost(target)+1
- rightmost(5)+1=5rightmost(5) + 1 = 5rightmost(5)+1=5,后任 a5=7a_5 = 7a5=7
- rightmost(4)+1=5rightmost(4) + 1 = 5rightmost(4)+1=5,后任 a5=7a_5 = 7a5=7
求最近邻居:
- 前任和后任距离更近者
