Leetcode.1040 移动石子直到连续 II

文章列表

题目链接

Leetcode.1040 移动石子直到连续 II Rating ： 2456

题目描述

在一个长度无限的数轴上，第 i颗石子的位置为 stones[i]。如果一颗石子的位置最小/最大，那么该石子被称作 端点石子 。

每个回合，你可以将一颗端点石子拿起并移动到一个未占用的位置，使得该石子不再是一颗端点石子。

值得注意的是，如果石子像 stones = [1,2,5]这样，你将无法移动位于位置 5 的端点石子，因为无论将它移动到任何位置（例如 0 或 3），该石子都仍然会是端点石子。

当你无法进行任何移动时，即，这些石子的位置连续时，游戏结束。

要使游戏结束，你可以执行的最小和最大移动次数分别是多少？以长度为 2 的数组形式返回答案：answer = [minimum_moves, maximum_moves]。

示例 1：

输入：[7,4,9]
输出：[1,2]
解释：
我们可以移动一次，4 -> 8，游戏结束。
或者，我们可以移动两次 9 -> 5，4 -> 6，游戏结束。

示例 2：

输入：[6,5,4,3,10]
输出：[2,3]
解释：
我们可以移动 3 -> 8，接着是 10 -> 7，游戏结束。
或者，我们可以移动 3 -> 7, 4 -> 8, 5 -> 9，游戏结束。
注意，我们无法进行 10 -> 2 这样的移动来结束游戏，因为这是不合要求的移动。

示例 3：

输入：[100,101,104,102,103]
输出：[0,0]

提示：

$3 <= stones.length <= 10^4$
$1 <= stones[i] <= 10^9$
stones[i]的值各不相同。

解法：排序 + 滑动窗口

一个端点移动之后，不能还是端点。
当端点移动之后，整个区间的范围必然会缩小。
当不能移动的时候，整个区间必然有序。

最大移动次数：

由于每次移动端点，都会缩减区间长度。为了使 移动次数最大，我们考虑让 每次区间缩减的长度尽可能的小，比如每次都缩减 1。

左端点向右边的空闲位置移动：

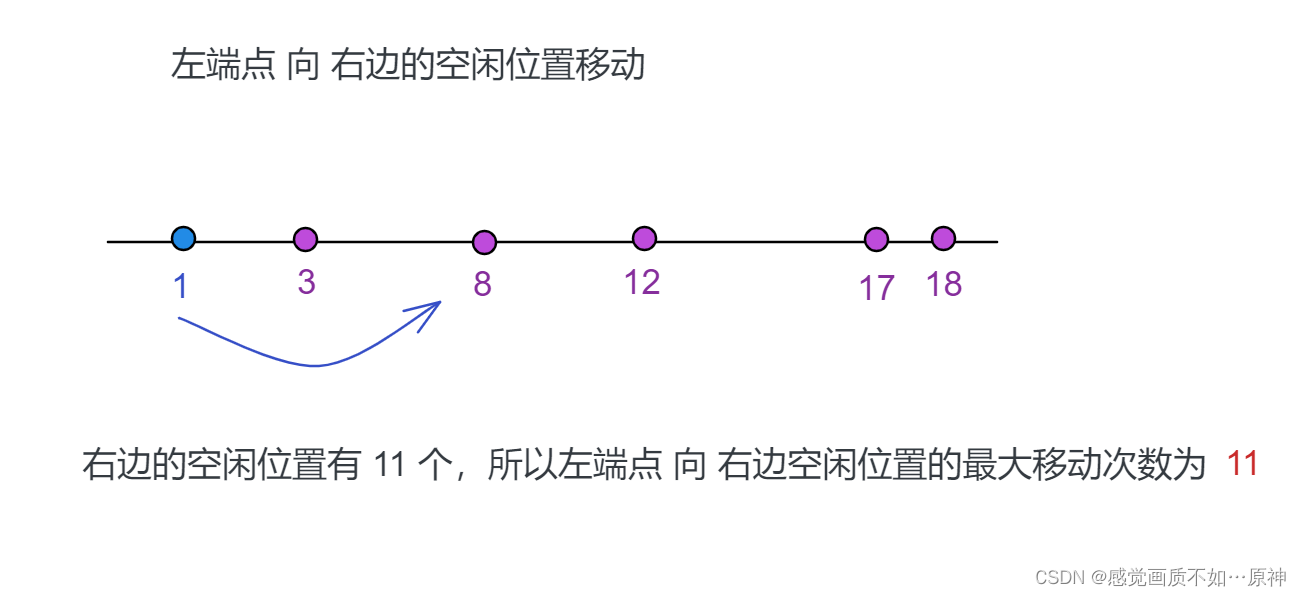
Leetcode.1040 移动石子直到连续 II

右端点向左边的空闲位置移动：

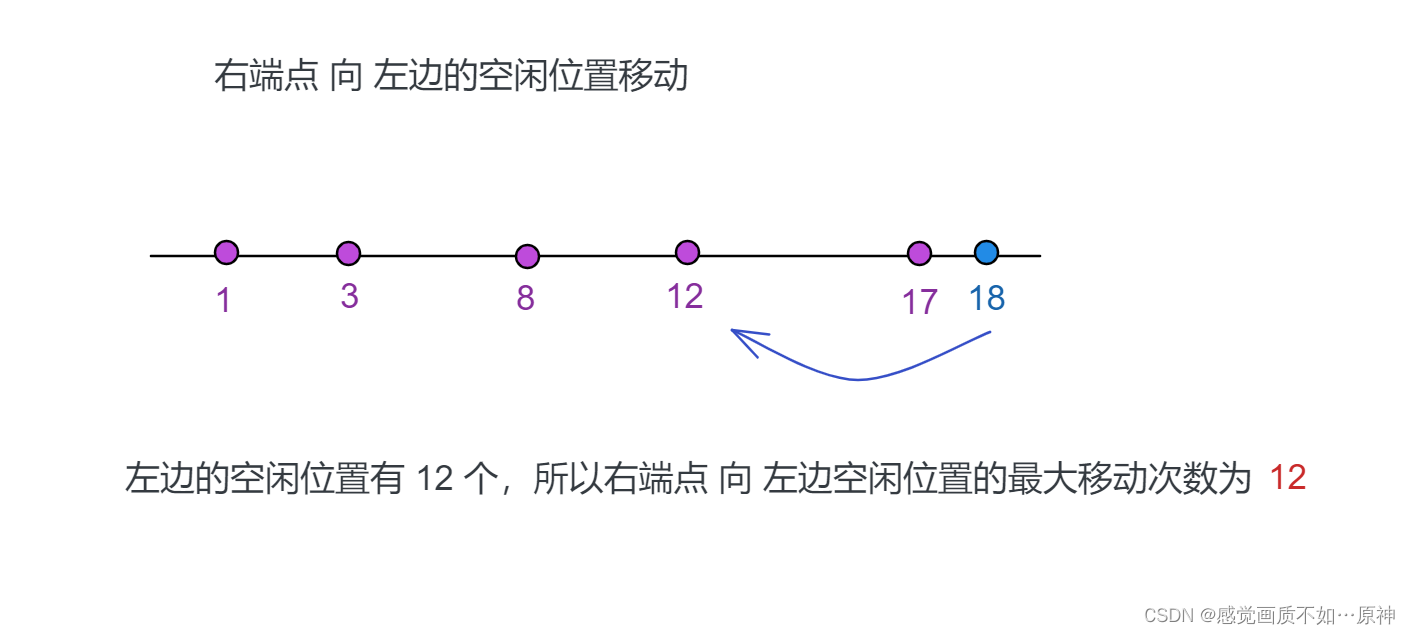
Leetcode.1040 移动石子直到连续 II

所以两者取最大值，即最大的移动次数为 $max\\{11 , 12 \\} = 12$ 。

右边的空闲位置数量 $d 1 = s [n - 1] - s [1] - n + 2$
左边的空闲位置数量 $d 2 = s [n - 2] - s [0] - n + 2$
最大移动次数 $mx = max \\{ d1 , d2 \\}$

最小移动次数：

特殊情况：

如果左边或者右边的空闲位置为 0 ，也就是左边或者右边的所有点都连续，即 $d 1 = 0∣∣ d 2 = 0$ ，最小移动次数就为 $mi = min \\{ 2 , mx \\}$

一般情况：

stones的 size为 n。因为到最后必然是 n个连续的数（就是 $d = 1$ 的等差数列），所以我们只需要维护一个长度为 n的窗口，更新不超过窗口长度 n的最大元素个数 max_count。

所以，最小的移动次数就为 $mi = n - max\\_count$ 。

最后返回 ${ mi , mx \\}$ 即可。

时间复杂度： $O (n l o g n)$

C++代码：

class Solution {
public:vector<int> numMovesStonesII(vector<int>& s) {sort(s.begin(),s.end());int n  = s.size();int p1 = s[n - 2] - s[0] - n + 2 , p2 = s[n - 1] - s[1] - n + 2;int mx = max(p1,p2);if(p1 == 0 || p2 == 0){return {min(2 , mx) , mx};}int max_count = 0;for(int i = 0,j = 0;j < n;j++){while(s[j] - s[i] + 1 > n){i++;}max_count = max(max_count , j - i + 1);}int mi = n - max_count;return {mi,mx};}
};

Python代码：

class Solution:def numMovesStonesII(self, s: List[int]) -> List[int]:s.sort()n = len (s)d1 = s[-2] - s[0] - n + 2d2 = s[-1] - s[1] - n + 2mx = max(d1,d2)if d1 == 0 or d2 == 0:return [min(2 , mx) , mx]max_count , i = 0 , 0for j in range(0,n):while s[j] - s[i] + 1 > n:i = i + 1max_count = max(max_count,j - i + 1)mi = n - max_countreturn [mi,mx]

Leetcode.1040 移动石子直到连续 II

题目链接