题目描述

原题链接：583. 两个字符串的删除操作

解题思路

（1）基于求最长公共子序列思路

本题与 1143. 最长公共子序列 的区别在于，1143中求的是两个序列中的最长公共子序列，而本题是要找到最少删除多少个元素后可以得到公共子序列。实际上，如果要找到删除元素最少，也就是要找到一个最长公共子序列，然后用两个序列的之和减去最长公共子序列长度的二倍，即可得到最少删除的元素个数。

class Solution {
public:int minDistance(string word1, string word2) {int n1 = word1.size(), n2 = word2.size();vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));int res = n1 + n2;for(int i = 1; i <= n1; i++) {for(int j = 1; j <= n2; j++) {if(word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}res -= 2 * dp[n1][n2];return res;}
};

（2）直接得到最少删除元素个数dp

115. 不同的子序列中相当于是只能删除一个字符串中的元素，而本题是两个字符串中的元素都可以删除。

• 动态规划五步曲：

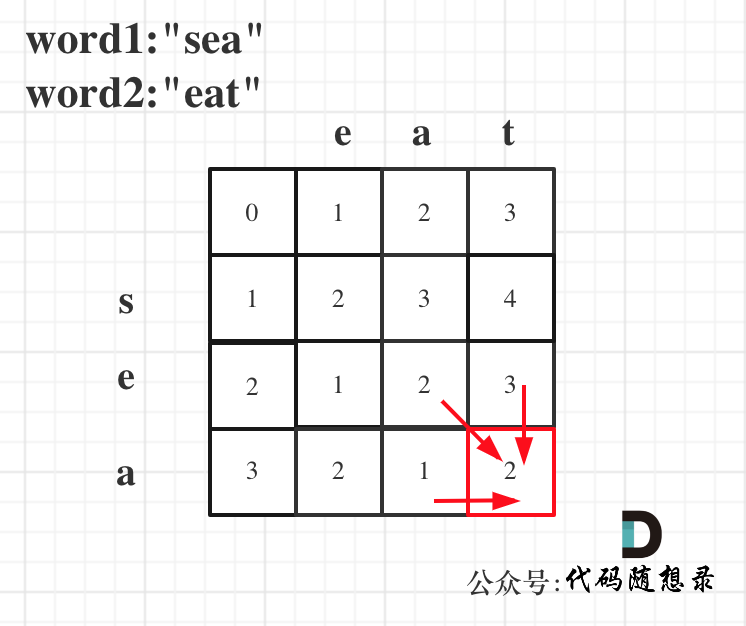
（1）dp[i][j]含义： 以word1[i - 1]和word2[j - 1]为结尾的字符串，最少删除元素的个数。

（2）递归公式： 当word1[i - 1] == word2[j - 1]时，dp[i][j] = dp[i - 1][j - 1]，从上一个状态转移古来。当不等时，dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2)，分别试着删除一个和两个，由于前方删除一个的情况都已经含义删除两个时加上二的情况，所以只用写dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)即可。

（3）dp数组初始化： dp[i][0] = dp[0][i] = i，删除个数。

（4）遍历顺序： 从左到右，从上到下。

（5）举例：

class Solution {
public:int minDistance(string word1, string word2) {int n1 = word1.size(), n2 = word2.size();vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));for(int i = 0; i <= n1; i++)            dp[i][0] = i;for(int i = 1; i <= n2; i++)            dp[0][i] = i;for(int i = 1; i <= n1; i++) {for(int j = 1; j <= n2; j++) {if(word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);}}}return dp[n1][n2];}
};

参考文章：583. 两个字符串的删除操作