leetcode究极刷题笔记（16~20）

（16）最接近的三数之和（中等）

实现思路：
本题与前文讲的三数之和有相同之处，但是本题求的是最接近的三数之和，所以我们这里可以使用键值对来映射对应的差值与值的关系，从而达到目的。

代码实现如下：

class Solution {
public:int threeSumClosest(vector<int>& nums, int target) {sort(nums.begin(),nums.end());pair<int,int> res(INT_MAX,INT_MAX);for(int i=0;i<nums.size();i++){for(int j=i+1,k=nums.size()-1;j<k;j++){while(k-1>j && nums[i]+nums[j]+nums[k-1]>=target) k--;int s=nums[i]+nums[j]+nums[k];res=min(res,make_pair(abs(s-target),s));if(k-1>j){s=nums[i]+nums[j]+nums[k-1];res=min(res,make_pair(target-s,s));//pair比较的时候是先比较第一个参数，如果二者相同在比较第二个参数}}}return res.second;}
};

（17）电话号码的组合（中等）

实现思路：
对于这种排列组合的问题，我们最先想到的就是dfs，首先在这里引入一个例题（具体题目可以自Acwing上搜索排序数字）

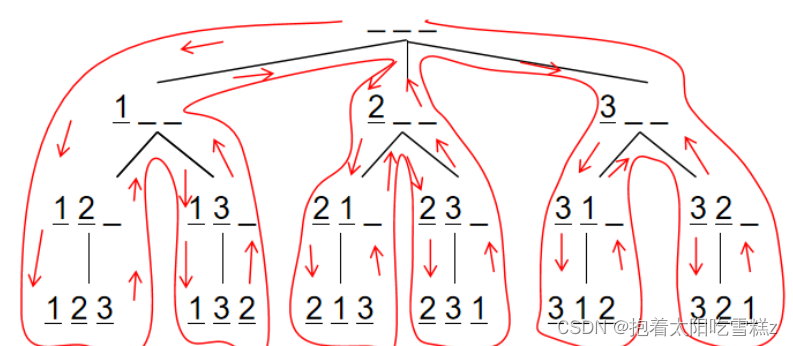
eg、排列数字

题目描述：

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

实现思路：
对于上述问题，我们可以这样进行排列：

 

假设有 3 个空位，从前往后填数字，每次填一个位置，填的数字不能和前面一样。

最开始的时候，三个空位都是空的：__ __ __

首先填写第一个空位，第一个空位可以填 1，填写后为：1 __ __

填好第一个空位，填第二个空位，第二个空位可以填 2，填写后为：1 2 __

填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为： 1 2 3

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：1 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3 ，没有其他数字可以填。

因此再往后退一步，退到了状态：1 __ __。第二个空位上除了填过的 2，还可以填 3。第二个空位上填写 3，填写后为：1 3 __

填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为： 1 3 2

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：1 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。

因此再往后退一步，退到了状态：1 __ __。第二个空位上除了填过的 2，3，没有其他数字可以填。

因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，还可以填 2。第一个空位上填写 2，填写后为：2 __ __

填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：2 1 __

填好第二个空位，填第三个空位，第三个空位可以填 3，填写后为：2 1 3

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：2 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 3，没有其他数字可以填。

因此再往后退一步，退到了状态：2 __ __。第二个空位上除了填过的 1，还可以填 3。第二个空位上填写 3，填写后为：2 3 __

填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：2 3 1

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：2 3 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，没有其他数字可以填。

因此再往后退一步，退到了状态：2 __ __。第二个空位上除了填过的 1，3，没有其他数字可以填。

因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，2，还可以填 3。第一个空位上填写 3，填写后为：3 __ __

填好第一个空位，填第二个空位，第二个空位可以填 1，填写后为：3 1 __

填好第二个空位，填第三个空位，第三个空位可以填 2，填写后为：3 1 2

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：3 1 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 2，没有其他数字可以填。

因此再往后退一步，退到了状态：3 __ __。第二个空位上除了填过的 1，还可以填 2。第二个空位上填写 2，填写后为：3 2 __

填好第二个空位，填第三个空位，第三个空位可以填 1，填写后为：3 2 1

这时候，空位填完，无法继续填数，所以这是一种方案，输出。

然后往后退一步，退到了状态：3 2 __ 。剩余第三个空位没有填数。第三个空位上除了填过的 1，2，没有其他数字可以填。

因此再往后退一步，退到了状态：3 __ __。第二个空位上除了填过的 1，2，没有其他数字可以填。

因此再往后退一步，退到了状态：__ __ __。第一个空位上除了填过的 1，2，3，没有其他数字可以填。

注：以上内容均转载自Acwing——Hasity的题解

代码实现如下：

#include<iostream>
using namespace std;
const int N=100010;
int n;
int a[N];
bool st[N];
void dfs(int u)
{if(u==n){for(int i=0;i<n;i++){cout <<a[i] << ' ';}cout <<endl;}for(int i=1;i<=n;i++){if(!st[i]){a[u]=i;st[i]=true;dfs(u+1);st[i]=false;}}
}
int main()
{cin >> n;dfs(0);return 0;
}

所以我们可以利用上述问题的思路对这个问题进行求解：

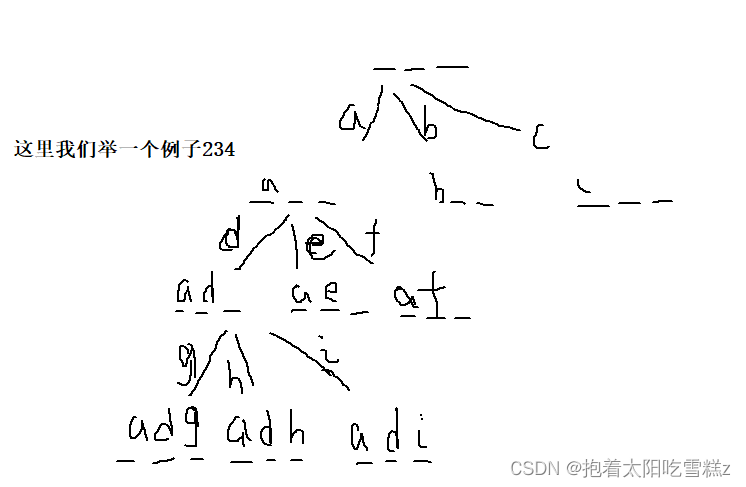
 具体实现代码如下：

class Solution {
public:vector<string> ans;string strs[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};void dfs(string&digits,int u,string path){if(u==digits.size()){ans.push_back(path);}else{for(auto c:strs[digits[u]-'0'])dfs(digits,u+1,path+c);}}vector<string> letterCombinations(string digits) {if(digits.empty()){return {};}dfs(digits,0,"");return ans;}
};

（18）四数之和（中等）

实现思路：

思路与三数相加类似

代码实现思路如下：

class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {sort(nums.begin(),nums.end());vector<vector<int>> res;for(int i=0;i<nums.size();i++){if(i && nums[i]==nums[i-1]) continue;for(int j=i+1;j<nums.size();j++){if(j>i+1 && nums[j]==nums[j-1]) continue;for(int k=j+1,u=nums.size()-1;k<u;k++){if(k>j+1 && nums[k]==nums[k-1]) continue;while(u-1>k && (long)nums[i]+nums[j]+nums[u-1]+nums[k]>=target) u--;if((long)nums[i]+nums[j]+nums[u]+nums[k]==target){res.push_back({nums[i],nums[j],nums[k],nums[u]});}}}}return res;}
};

（19）删除链表倒数第k个节点（中等）

实现思路：
本题实现思路十分简单，我们首先遍历链表得到对应的链表的长度k，因为我们要删除的是倒数第n个节点，所以我们正向删除的就是第k-n个节点，我们找到第k-n-1个节点，将其对应的关系联络起来就可以了。

代码实现如下：（注：对应这种头结点未必存在的问题，我们最好使用哨兵位记录头结点的位置）

class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {auto dummy=new ListNode(-1);dummy->next=head;int k=0;for(auto p=dummy;p;p=p->next){k++;}auto p=dummy;for(int i=0;i<k-n-1;i++ ) p=p->next;p->next=p->next->next;return dummy->next;}
};

（20）有效的括号（简单）

实现思路：
因为我们要匹配左右括号之间的关系，所以我们可以创建一个栈，如果是左括号就入栈，如果此时右括号与之相匹配的话就删除栈顶与之相对应的左括号（我们观察ASCII表会发现，左右括号ASCII的差最多不超过2，所以我们可以利用此条件判断是否匹配）。

代码实现如下：

class Solution {
public:bool isValid(string s) {stack<char> st;for(auto str:s){if(str=='(' || str=='[' || str=='{') st.push(str);else if(st.size() && abs(st.top()-str)<=2) st.pop();else return false;}return st.empty();}
};

希望以上文章对您有帮助！！！