代码随想录_二叉树_leetcode236

在计算机科学的领域里，二叉树是一种非常重要的数据结构。它有着广泛的应用，比如在算法设计、编译器设计、人工智能等地方。而在二叉树的应用中，找到两个节点的最近公共祖先（Lowest Common Ancestor, LCA）是一个常见的问题。本文将以LeetCode上的两个题目为例，探讨二叉树和二叉搜索树中寻找最近公共祖先的方法。

问题引入：LeetCode 236. 二叉树的最近公共祖先

给定一个二叉树，找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义是一个节点，它既是两个给定节点的祖先，又在树上尽可能的深。

示例分析

示例 1:

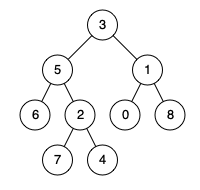
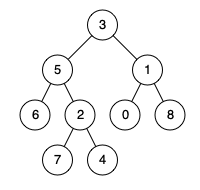
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。

代码实现

// leetcode 236. 二叉树的最近公共祖先
// 回溯
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr || root == p || root == q) {
            return root;
        }
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if (left != nullptr && right != nullptr) {
            return root;
        }
        return left ? left : right;
    }
};

相关问题：LeetCode 235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树，找到该树中两个指定节点的最近公共祖先。二叉搜索树的性质是左子树所有节点都小于根节点，右子树所有节点都大于根节点。

示例分析

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2。

代码实现

// leetcode 235. 二叉搜索树的最近公共祖先
// 层序遍历第一个在pq之间的节点
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        int a = min(p->val, q->val);
        int b = max(p->val, q->val);
        queue que;
        que.push(root);
        while (!que.empty()) {
            TreeNode* cur = que.front();
            que.pop();
            if (cur->val >= a && cur->val <= b) {
                return cur;
            }
            if (cur->left) que.push(cur->left);
            if (cur->right) que.push(cur->right);
        }
        return nullptr;
    }
};

深入思考

通过这两个问题，我们可以看到寻找二叉树和二叉搜索树最近公共祖先的方法有所不同。在二叉树中，我们需要通过递归的方式从底向上进行查找；而在二叉搜索树中，由于其有序的性质，我们可以通过层序遍历的方法来快速找到最近公共祖先。

进一步思考，如果我们将这两个问题进行对比，可以得出以下结论：

• 二叉树的LCA问题需要通过递归的方式，利用左右子树的信息来确定当前节点的LCA。
• 二叉搜索树的LCA问题可以利用其有序性，通过层序遍历的方式快速找到LCA。

这种差异化的处理方式，反映了不同数据结构在解决特定问题时的优势和局限性。希望通过对这两个问题的探讨，能够加深对二叉树和二叉搜索树的理解，以及如何选择合适的方法来解决相关问题。

leetcode 236. 二叉树的最近公共祖先

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点3 。

示例 2：

 

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

 代码

//leetcode 236. 二叉树的最近公共祖先
// 回溯
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == nullptr || root == p || root == q){return root;}TreeNode* left = lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p, q);if (left != nullptr && right != nullptr){return root;}return left ? left : right;}
};

leetcode 235. 二叉搜索树的最近公共祖先

235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

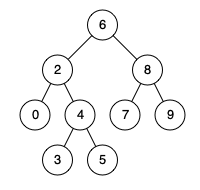
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2和节点 4的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

 

 代码

// leetcode 235. 二叉搜索树的最近公共祖先
// 层序遍历第一个在pq之间的结点
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {int a = min(p->val, q->val);int b = max(p->val, q->val);queue<TreeNode*> que;que.push(root);while (!que.empty()){TreeNode* cur = que.front();que.pop();if (cur->val >= a && cur->val <= b)return cur;if (cur->left)que.push(cur->left);if (cur->right)que.push(cur->right);}return NULL;}
};