数据结构与算法基础-学习-17-二叉树之哈夫曼树

一、哈夫曼树

1、知识点引入

我们在实现例如学生成绩划分时，实现思路如下图，假设得A的同学占10%，得B的同学占20%，得C的同学占30%，得D的同学占40%，一共10000个学生。得A的判断10000人*1次*10%（单位：次），得B的判断10000人*2次*50%（单位：次），得C的判断10000人*3次*10%（单位：次），得D的判断10000人*3次*30%（单位：次），一共需要判断1000+10000+3000+9000=23000次。

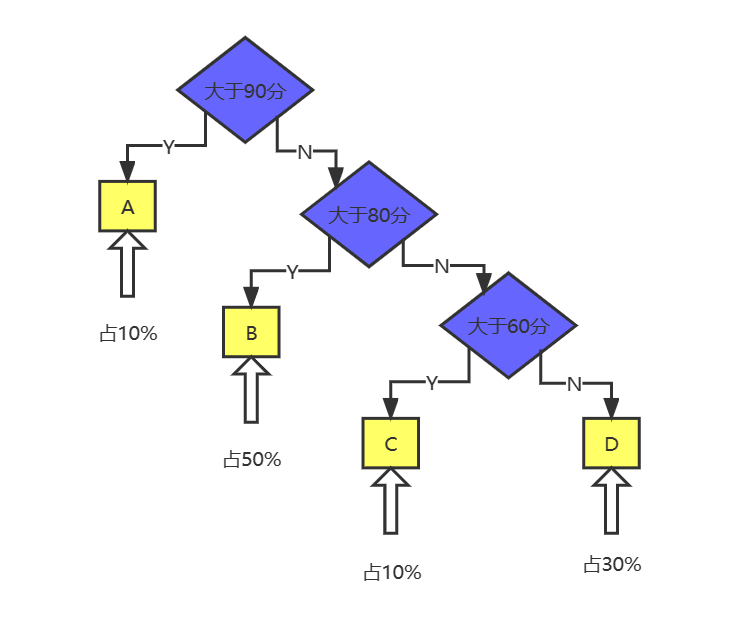
如果我们将判断逻辑变化一下，如下图，得A的判断10000人*2次*10%（单位：次），得B的判断10000人*2次*50%（单位：次），得C的判断10000人*2次*10%（单位：次），得D的判断10000人*2次*30%（单位：次），一共需要判断2000+10000+2000+6000=20000次。比原来少了3000次判断。其实这个并不是最优的解，我们来了解一下哈夫曼树是怎么解决类似得问题。

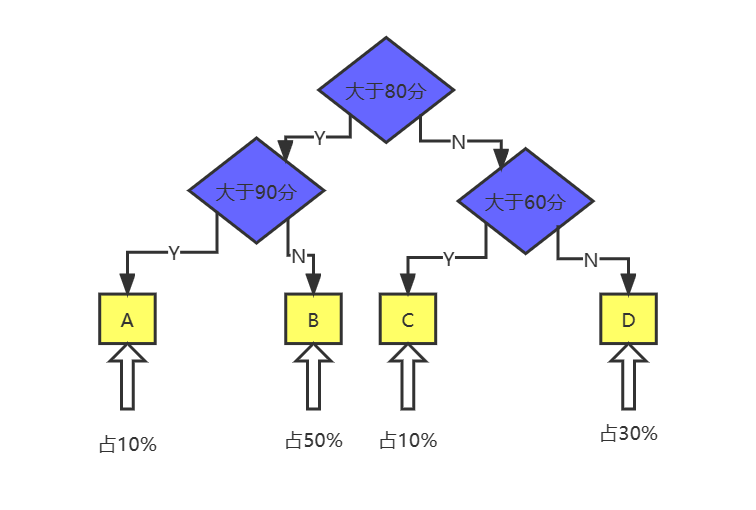
2、概念

2.1路径

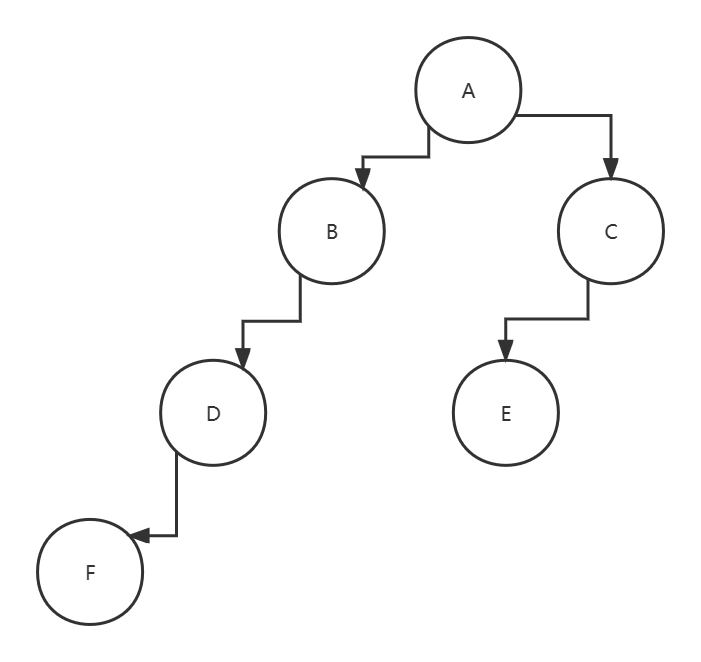
从树中一个结点到另一个结点之间的分支构成这个两个结点间的路径。

2.2结点的路径长度

两结点间路径上的分支数。

A->B = 1

A->C = 1

A->D = 2

A->E = 2

A->F = 3

2.3树根到每一个结点的路径长度之和。

TL（TREE LENGTH）= 0 + 1 + 1 + 2 + 2 + 3 = 9

2.4权

将树中结点赋予一个有含义的数值，这个数值称为结点的权。

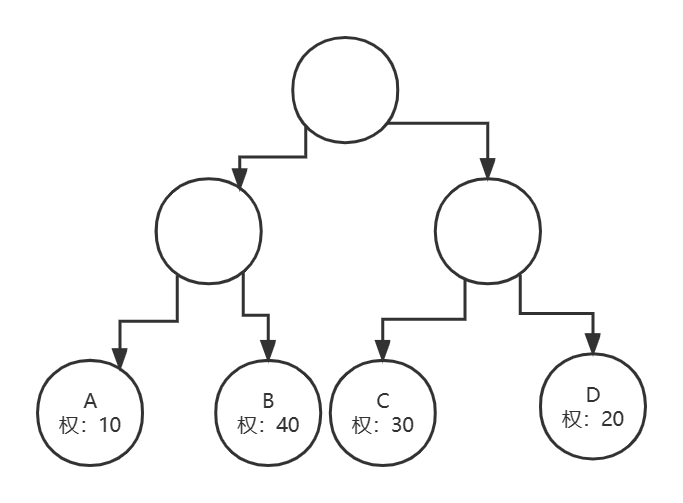
2.5结点的带权路径长度

从根结点到该结点之间的路径长度与该节点的权乘积。

A的带权路径长度：2 * 10 = 20

B的带权路径长度：2 * 40 = 80

C的带权路径长度：2 * 30 = 60

D的带权路径长度：2 * 20 = 40

2.6树的带权路径长度

树中所有叶子结点的带权路径长度之和。

上面图中树的带权路径长度：200

2.7最优树

哈夫曼树是带权路径长度最短的树，只有度相同的情况下才是，例如二叉树中哈夫曼树是最优二叉树，三叉树中哈夫曼树是最有三叉树。

3、结构体定义

typedef unsigned long long HaffmanTreeLentype;typedef struct HaffmanNode
{HaffmanTreeLentype Weight;HaffmanTreeLentype ParentIndex;HaffmanTreeLentype LeftChildIndex;HaffmanTreeLentype RightChildIndex;
}HTNode, *HaffmanTree;

4、函数实现

4.1找最小的两个值

（1）定义

Status Select2MinVal(HaffmanTree HT, HaffmanTreeLentype MaxBorderIndex,HaffmanTreeLentype* MinValIndex1, HaffmanTreeLentype* MinValIndex2)
{JudgeAllNullPointer(HT);HaffmanTreeLentype i;*MinValIndex1 = 0;*MinValIndex2 = 0;for(i = 1; i <= MaxBorderIndex; i++){if(HT[i].ParentIndex != 0){continue;}if(*MinValIndex1 == 0){*MinValIndex1 = i;continue;}if(*MinValIndex2 == 0){if(HT[i].Weight > HT[*MinValIndex1].Weight)//MinValIndex1第二小，MinValIndex2第一小{*MinValIndex2 = *MinValIndex1;*MinValIndex1 = i;             }else{*MinValIndex2 = i;}break;}}//printf("MID, MinValIndex1 : %lld, MinValIndex2 : %lld\\n",*MinValIndex1,*MinValIndex2);for(i = ((*MinValIndex1) > (*MinValIndex2) ? (*MinValIndex1) : (*MinValIndex2)) + 1; i <= MaxBorderIndex; i++){if(HT[i].ParentIndex != 0)//有父节点的跳过{continue;}if(HT[i].Weight >= HT[*MinValIndex1].Weight)//比第二小的大跳过{continue;}if(HT[i].Weight >= HT[*MinValIndex2].Weight)//比第二小的小，比第一小的大或等于{*MinValIndex1 = i;}else//比第二小的小{*MinValIndex1 = *MinValIndex2;*MinValIndex2 = i;}    }//printf("FIN, MinValIndex1 : %lld, MinValIndex2 : %lld\\n",*MinValIndex1,*MinValIndex2);return SuccessFlag;
}

（2）参数

（3）实现思路

这个就不讲了不难，注释也很通俗易懂。

4.2创建哈夫曼树

（1）定义

Status CreateHaffmanTree(HaffmanTree* HT, HaffmanTreeLentype* Array, HaffmanTreeLentype ArrayLen)
{if(ArrayLen <= 1){Log("CreateHaffmanTree Function ArrayLen need > 1.",Error);return FailFlag;}// INIT HAFFMANHaffmanTreeLentype HaffmanTreeLen = ArrayLen * 2;//ArrayLen个叶子结点，需要合并ArrayLen-1次，一共ArrayLen * 2 - 1个结点，0号位不用，所以是ArrayLen * 2。*HT = (HaffmanTree)MyCalloc(HaffmanTreeLen, sizeof(HTNode));HaffmanTreeLentype i;for(i = 1; i <= ArrayLen; i++){(*HT)[i].Weight = Array[i - 1];}//PADDING HAFFMANHaffmanTreeLentype MinValIndex1 = 0;HaffmanTreeLentype MinValIndex2 = 0;for(i = ArrayLen + 1; i < HaffmanTreeLen; i++){Select2MinVal(*HT, i - 1, &MinValIndex1, &MinValIndex2);(*HT)[i].LeftChildIndex         = MinValIndex2;(*HT)[i].RightChildIndex        = MinValIndex1;(*HT)[i].Weight                 = (*HT)[MinValIndex1].Weight + (*HT)[MinValIndex2].Weight;(*HT)[MinValIndex1].ParentIndex = i;(*HT)[MinValIndex2].ParentIndex = i;} Log("Create HaffmanTree     : OK\\n",Info);return SuccessFlag;    
}

（2）参数

（3）实现思路

例如权值数组为：

HaffmanTreeLentype WeightArray[]  = {5,6,2,9,7};

我们将他转换成哈夫曼树（用数组实现这里），一共有5个权值，也就是叶子节点，需要5-1个非叶子节点，加上一个0号位不用，需要初始化一个长度为10的数组，我们再将权值添加上去，如下：

[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 5      | 0           | 0              | 0               ]
[ 2     | 6      | 0           | 0              | 0               ]
[ 3     | 2      | 0           | 0              | 0               ]
[ 4     | 9      | 0           | 0              | 0               ]
[ 5     | 7      | 0           | 0              | 0               ]
[ 6     | 0      | 0           | 0              | 0               ]
[ 7     | 0      | 0           | 0              | 0               ]
[ 8     | 0      | 0           | 0              | 0               ]
[ 9     | 0      | 0           | 0              | 0               ]

然后我们开始组合先找出最小的两个值5和2，等于7，我们放到索引为6的位置上，将左孩子的索引和右孩子的索引加上，5和2的父母索引加上。

[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 5      | 6           | 0              | 0               ]
[ 2     | 6      | 0           | 0              | 0               ]
[ 3     | 2      | 6           | 0              | 0               ]
[ 4     | 9      | 0           | 0              | 0               ]
[ 5     | 7      | 0           | 0              | 0               ]
[ 6     | 7      | 0           | 3              | 1               ]
[ 7     | 0      | 0           | 0              | 0               ]
[ 8     | 0      | 0           | 0              | 0               ]
[ 9     | 0      | 0           | 0              | 0               ]

再从索引位1-6找且父母索引为0中找，发现2号位的6和5号位的7最小，加起来是13放到7号位，将左孩子的索引和右孩子的索引加上，6和7的父母索引加上。

[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 5      | 6           | 0              | 0               ]
[ 2     | 6      | 7           | 0              | 0               ]
[ 3     | 2      | 6           | 0              | 0               ]
[ 4     | 9      | 0           | 0              | 0               ]
[ 5     | 7      | 7           | 0              | 0               ]
[ 6     | 7      | 0           | 3              | 1               ]
[ 7     | 13     | 0           | 2              | 5               ]
[ 8     | 0      | 0           | 0              | 0               ]
[ 9     | 0      | 0           | 0              | 0               ]

再从索引位1-7找且父母索引为0中找，发现6号位的7和4号位的9最小，加起来是16放到8号位，将左孩子的索引和右孩子的索引加上，7和9的父母索引加上。

[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 5      | 6           | 0              | 0               ]
[ 2     | 6      | 7           | 0              | 0               ]
[ 3     | 2      | 6           | 0              | 0               ]
[ 4     | 9      | 8           | 0              | 0               ]
[ 5     | 7      | 7           | 0              | 0               ]
[ 6     | 7      | 8           | 3              | 1               ]
[ 7     | 13     | 0           | 2              | 5               ]
[ 8     | 16     | 0           | 6              | 4               ]
[ 9     | 0      | 0           | 0              | 0               ]

再从索引位1-8找且父母索引为0中找，发现7号位的13和8号位的16最小，加起来是29放到9号位，将左孩子的索引和右孩子的索引加上，13和16的父母索引加上。

[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 5      | 6           | 0              | 0               ]
[ 2     | 6      | 7           | 0              | 0               ]
[ 3     | 2      | 6           | 0              | 0               ]
[ 4     | 9      | 8           | 0              | 0               ]
[ 5     | 7      | 7           | 0              | 0               ]
[ 6     | 7      | 8           | 3              | 1               ]
[ 7     | 13     | 9           | 2              | 5               ]
[ 8     | 16     | 9           | 6              | 4               ]
[ 9     | 29     | 0           | 7              | 8               ]

哈夫曼树会先把权值数组中的每个元素变成一个根节点，每次找出两个最小的根结点，合并成一棵树，再进行组合，以此类推得到如下的结果，也就是说权值高的结点接近根结点，权值低的反之。

4.3销毁哈夫曼树

（1）定义

Status DestoryHaffmanTree(HaffmanTree HT)
{JudgeAllNullPointer(HT);free(HT);HT = NULL;Log("Destory HaffmanTree    : OK\\n",Info);return SuccessFlag;
}

（2）参数

二、LInux测试

[gbase@czg2 Tree]$ make
gcc -Wall -g ../Log/Log.c BinaryTree.c HaffmanTree.c main.c -o TestBinaryTree -I ../Log/[gbase@czg2 Tree]$ ./TestBinaryTree 
2023-3--[Info]--Init Global Array      : OK
2023-3--[Info]--Init Binary Tree       : OK
2023-3--[Info]--New Binary Search Tree : OK
2023-3--[Info]--PreOrderTraverse       : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse        : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse      : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7
2023-3--[Info]--PreOrderTraverseNoRcs  : [6 ,3 ,2 ,1 ,5 ,8 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverseNoRcs   : [1 ,2 ,3 ,5 ,6 ,7 ,8 ], CurSize : 7
2023-3--[Info]--PostOrderTraverseNoRcs : [1 ,2 ,5 ,3 ,7 ,8 ,6 ], CurSize : 7
2023-3--[Info]--LevelOrderBinaryTree   : [6 ,3 ,8 ,2 ,5 ,7 ,1 ], CurSize : 7
2023-3--[Info]--SqQueue Data           :
Data           : [1 ,2 ,3 ,0 ,0 ,4 ,5 ,0 ,6 ,0 ,0 ,7 ,0 ,0 ,0 ]
FrontIndex     : 0
RearIndex      : 15
SqQueueLen     : 15
2023-3--[Info]--Init Binary Tree       : OK
2023-3--[Info]--PreOrderTraverse       : [1 ,2 ,3 ,4 ,5 ,6 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse        : [3 ,2 ,5 ,6 ,4 ,7 ,1 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse      : [3 ,6 ,5 ,7 ,4 ,2 ,1 ], CurSize : 7
2023-3--[Info]--PreOrderTraverseNoRcs  : [1 ,2 ,3 ,4 ,5 ,6 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverseNoRcs   : [3 ,2 ,5 ,6 ,4 ,7 ,1 ], CurSize : 7
2023-3--[Info]--PostOrderTraverseNoRcs : [3 ,6 ,5 ,7 ,4 ,2 ,1 ], CurSize : 7
2023-3--[Info]--LevelOrderBinaryTree   : [1 ,2 ,3 ,4 ,5 ,7 ,6 ], CurSize : 7
2023-3--[Info]--Init Binary Tree       : OK
2023-3--[Info]--Copy Tree              : OK
2023-3--[Info]--PreOrderTraverse       : [1 ,2 ,3 ,4 ,5 ,6 ,7 ], CurSize : 7
2023-3--[Info]--InOrderTraverse        : [3 ,2 ,5 ,6 ,4 ,7 ,1 ], CurSize : 7
2023-3--[Info]--PostOrderTraverse      : [3 ,6 ,5 ,7 ,4 ,2 ,1 ], CurSize : 7
2023-3--[Info]--Tree Depth             : 4
2023-3--[Info]--Tree Depth             : 5
2023-3--[Info]--Tree Depth             : 5
2023-3--[Info]--Tree Node Num          : 7
2023-3--[Info]--Tree Node Num          : 7
2023-3--[Info]--Tree Node Num          : 7
2023-3--[Info]--Tree Leaves Node Num   : 3
2023-3--[Info]--Tree Leaves Node Num   : 3
2023-3--[Info]--Tree Leaves Node Num   : 3
2023-3--[Info]--Create HaffmanTree     : OK
2023-3--[Info]--HaffmanTree            :
[ Index | Weight | ParentIndex | LeftChildIndex | RightChildIndex ]
[ 0     | 0      | 0           | 0              | 0               ]
[ 1     | 5      | 6           | 0              | 0               ]
[ 2     | 6      | 7           | 0              | 0               ]
[ 3     | 2      | 6           | 0              | 0               ]
[ 4     | 9      | 8           | 0              | 0               ]
[ 5     | 7      | 7           | 0              | 0               ]
[ 6     | 7      | 8           | 3              | 1               ]
[ 7     | 13     | 9           | 2              | 5               ]
[ 8     | 16     | 9           | 6              | 4               ]
[ 9     | 29     | 0           | 7              | 8               ]
2023-3--[Info]--Destory HaffmanTree    : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK
2023-3--[Info]--Destroy BT Node        : OK