二叉搜索树（BST）真的是个神奇的家伙，看似简单的结构，却藏着无限的可能。你知道吗？它不仅是数据结构的“常青树”，更是面试题的“宠儿”。那么问题来了，为什么它如此受欢迎？

首先，BST的查找效率高得让人想鼓掌。因为它像是一个自动排序的“秘书”，左边小，右边大，帮你快速定位目标。但别高兴太早，如果树长得“歪七扭八”，查找效率可就大打折扣了。这就是为什么我们要关注树的平衡性，比如引入AVL树或红黑树来“扶正”它。

再来看看插入和删除操作。插入看似简单，但要确保不破坏BST的结构，得小心翼翼，像拼乐高一样，一块一块地放对位置。删除呢？更是复杂得像解谜题，得考虑多种情况：没有子节点、有一个子节点、有两个子节点。想象一下，如果你删错了，整个树的“秩序”可能就乱了。

最后，BST的应用场景无处不在。比如在数据库索引中，它帮助快速检索数据；在文本编辑器中，它助力自动补全功能。可以说，BST是个“多面手”，既能解决问题，又能让人陷入思考的深坑。

所以，下次当你遇到BST时，别只是机械地写代码，试着理解它的“内心世界”。你会发现，它不仅是一个工具，更是一种思维方式。就像人生，你需要不断调整平衡，才能走得更远。

🌈感谢阅读East-sunrise学习分享——[进阶数据结构]二叉搜索树
博主水平有限，如有差错，欢迎斧正🙏感谢有你 码字不易，若有收获，期待你的点赞关注💙我们一起进步

---

🌈我们在之前已经学习过了二叉树，而如今已经掌握C++语法的我们比起当初只能通过C语言学习已经稍有精进了
C++拥有一些C语言所不具有的优势，所以更适合我们对高阶数据结构的学习，今天要分享的二叉搜索树是二叉树的进阶类型，在做题或实际应用都有着重要地位🚀🚀🚀

一、概念

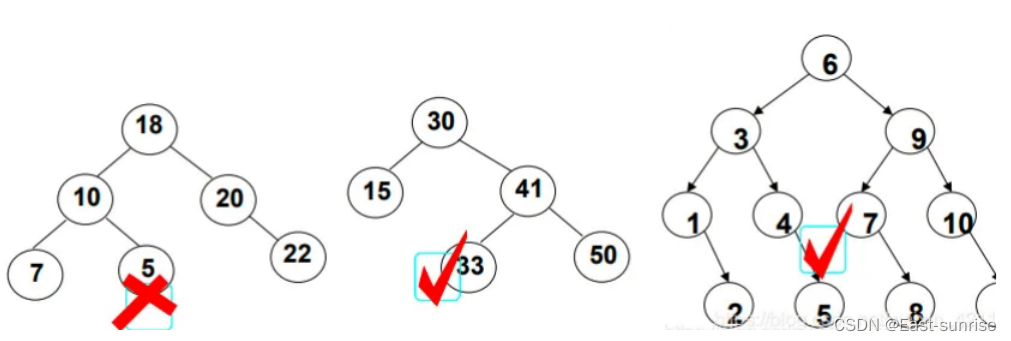
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

二、基本操作

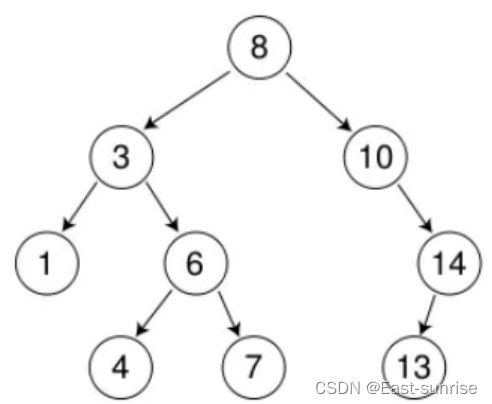
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};

2.1 查找

搜索二叉树的特性结构，使得它的查找效率十分快

• 从根开始比较、查找，比根大则往右边走查找，比根小则往左边走查找。
• 最多查找高度次，走到到空，还没找到，这个值不存在。

✏️代码实现

//查找
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}elsereturn true;}return false;
}

2.2 插入

插入的具体过程如下：

• 树为空，则直接新增节点，赋值给root指针
• 树不空，按二叉搜索树性质查找插入位置，插入新节点

由于要严格遵循二叉搜索树的结构，所以在每次遍历或最后的插入时都需要比较新增节点与其父节点的值的大小♨️所以我们可以用一个parent指针，随时记录下父节点，便于插入时的大小判断💭

✏️代码实现

//插入

bool Insert(const K& key)

{if (_root == nullptr){_root = new Node(key);return true;}//插入,小于就插左，大于就插右Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (key < cur->_key)cur = cur->_left;else if (key > cur->_key)cur = cur->_right;elsereturn false;}//到合适的空了，开始插入//要插在左还是右，还是需要比较cur = new Node(key);if (key < parent->_key)parent