算法模板

快速排序算法模板

void quick_sort(int q[], int l, int r)
{if (l >= r) return;int i = l - 1, j = r + 1, x = q[l + r >> 1]; // >> 表示按位右移，相当于进行÷2的运算，//同理， << 表示按位左移，相当于进行×2的运算while (i < j){do i ++ ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i], q[j]);}quick_sort(q, l, j), quick_sort(q, j + 1, r);
}

查找第k个数算法模板

int quick_find(int l,int r,int k){if(l == r) return q[l];int i = l-1, j = r+1;int x = q[ l+r >>1 ];while(i<j){while(q[ ++i ] < x);while(q[ --j ] > x);if(i<j) swap(q[i],q[j]);}int sl = j - l + 1;if(k<=sl) return quick_find(l,j,k);else return quick_find(j+1,r,k-sl);
}

模板题

快速排序

原题链接

https://www.acwing.com/problem/content/787/

题目

785 快速排序
给定你一个长度为 n 的整数数列。

请你使用快速排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1∼10^9 范围内），表示整个数列。

输出格式
输出共一行，包含 n 个整数，表示排好序的数列。

数据范围
1≤n≤100000
输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

题解

#include <iostream>
using namespace std;const int N = 1e6 + 10;int n;
int q[N];void quick_sort(int q[],int l,int r) {if(l>=r) return;int i = l-1,j=r+1;int x = q[l+r >>1];while(i<j) {do i++;while(q[i]<x);do j--;while(q[j]>x);if(i<j) swap(q[i],q[j]);}quick_sort(q,l,j);quick_sort(q,j+1,r);}
int main() {scanf("%d",&n);for(int i = 0; i < n; i++ ) scanf("%d",&q[i]);quick_sort(q,0,n-1);for(int i = 0; i < n; i++ ) printf("%d ",q[i]);return 0;}

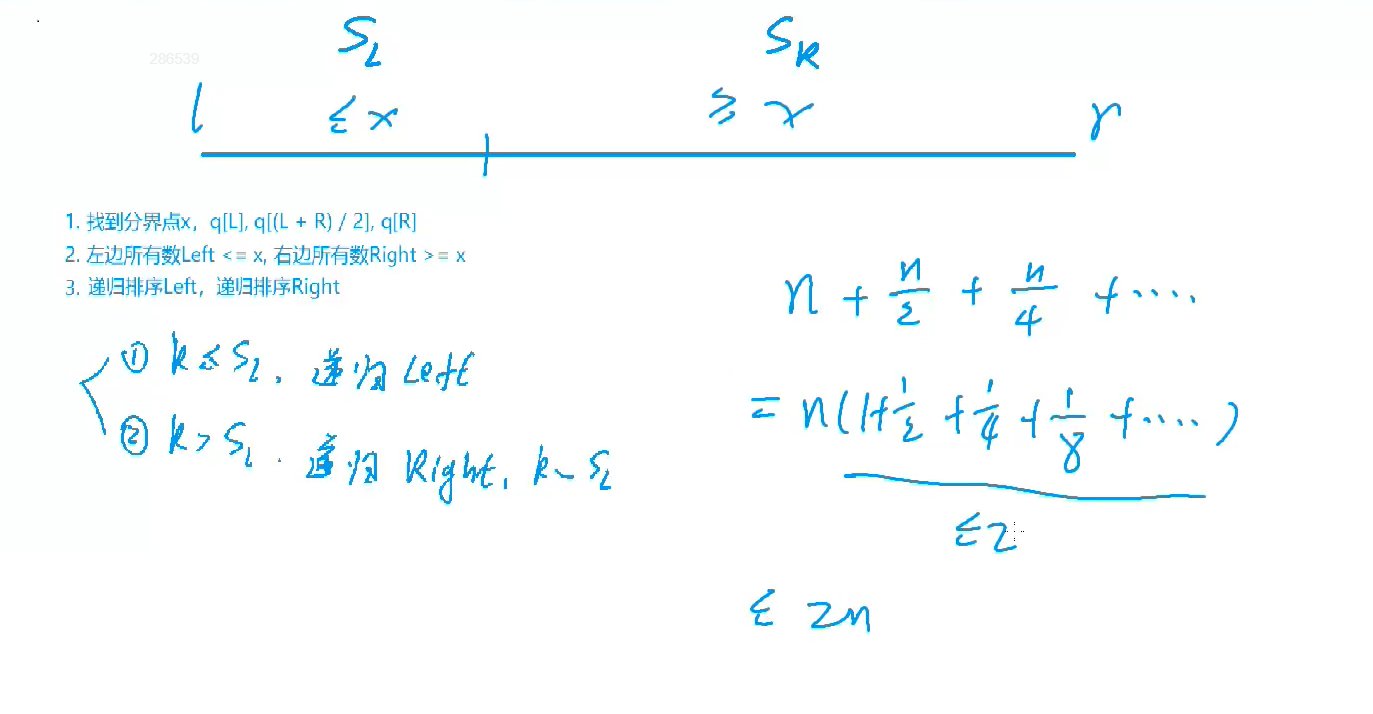
快速查找第k小的数

原题链接

https://www.acwing.com/problem/content/788/

题目

786 第k个数
给定一个长度为 n 的整数数列，以及一个整数 k，请用快速选择算法求出数列从小到大排序后的第 k 个数。

输入格式
第一行包含两个整数 n 和 k。

第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整数数列。

输出格式
输出一个整数，表示数列的第 k 小数。

数据范围
1≤n≤100000,
1≤k≤n
输入样例：

5 3
2 4 1 5 3

输出样例：

3

题解

#include <iostream>
//#include <bits/stdc++.h>
using namespace std;const int N = 1e6 + 10;int n,k;
int q[N];int quick_find(int l,int r,int k){if(l == r) return q[l];int i = l-1, j = r+1;int x = q[ l+r >>1];while(i<j){while(q[ ++i ] < x);while(q[ --j ] > x);if(i<j) swap(q[i],q[j]);}int sl = j - l + 1;if(k<=sl) return quick_find(l,j,k);else return quick_find(j+1,r,k-sl);
}int main(){scanf("%d%d",&n,&k);
//	cin>>n>>k;for(int i = 0; i < n; i++) scanf("%d",&q[i]);cout<<quick_find(0,n-1,k)<<endl;return 0;
}