1 前言

一直不太明白，α、β的赋值、判断比较具体怎么实现的，后来终于搞明白了，附上图记录一下。

如有帮助，请多多点赞！（阿里嘎多~）

2 基础知识

2.1 $\alpha 、\beta$的赋值

• 每一个max/min结点都拥有一对$\alpha 、\beta$。（看成struct数据结构吧）
• 初始化：
  • 根节点的$\alpha =-\infty 、\beta =+\infty$
  • 子节点的$\alpha 、\beta$等于父节点的$\alpha 、\beta$
• max结点的$\alpha =max(\alpha ,子节点)$
• min结点的$\beta =min(\beta ,子节点)$

2.2 max/min结点的值

• 叶子节点的值就是自己的值本身
• 不考虑剪枝的情况下，max结点的值=max(子节点x1、x2、x3…)
• 不考虑剪枝的情况下，min结点的值=min(子节点x1、x2、x3…)
• 剪枝的max/min结点的值不用计算，此时结点的值是一个取值范围。（为什么不用？因为剪枝就表明了这支没用了）

注意：max/min结点的$\alpha 、\beta$的值和自己的值不一定相等！！

2.3 判断规则

• 什么时候比较max/min结点$\alpha 、\beta$ 和 其子节点的值呢？
  从子节点开始回溯的时候。

• 当子节点x1带着自己的值从下往上回溯到max结点时，我们就需要判断：
  ifx1≥β,剪枝。(x2,x3,...全部剪枝)elseα=max(α，x1)继续搜索子节点x2if \\ \\ \\ x_1≥β,剪枝。(x_2,x_3,...全部剪枝) \\\\ else \\ \\ \\ α=max(α，x_1) \\ \\ \\ 继续搜索子节点x_2if   x1​≥β,剪枝。(x2​,x3​,...全部剪枝)else   α=max(α，x1​)   继续搜索子节点x2​
• 当子节点x1带着自己的值从下往上回溯到min结点时，我们就需要判断：
  ifx1≤α,剪枝。(x2,x3,...全部剪枝)elseβ=max(β，x1)继续搜索子节点x2if \\ \\ \\ x_1≤α,剪枝。(x_2,x_3,...全部剪枝) \\\\ else \\ \\ \\ β=max(β，x_1) \\ \\ \\ 继续搜索子节点x_2if   x1​≤α,剪枝。(x2​,x3​,...全部剪枝)else   β=max(β，x1​)   继续搜索子节点x2​

2.4 步骤

1. 初始化根节点的$\alpha =-\infty 、\beta =+\infty$
2. 开始深度搜索，将根节点的$\alpha =-\infty 、\beta =+\infty$赋给沿途结点的$\alpha 、\beta$
3. 当搜索到叶子结点时，就开始回溯，每次回溯需要进行判断也就是上述2.3节的内容。
4. 搜索完一个max/min结点的子节点后，就应该计算出该max/min结点的值，也就是上述2.2结点的内容，然后将自己回溯，重复步骤3。

2.5 总结

综上所述，这里存在很多计算、比较，我用简单的语言再阐述一遍：

1. 父节点的$\alpha 、\beta$赋值给子节点$\alpha 、\beta$（max/min结点才会有$\alpha 、\beta$）
2. 遇到非max/min结点，就带着这个值回溯
3. 回溯遇到了max/min结点，就和max/min结点的$\alpha 、\beta$的值进行比较：
   a. 如果满足剪枝条件，那就该max/min结点的子节点都不用搜索了，此时max/min结点直接返回。
   b. 如果不满足剪枝条件，那么就用这个值更新max/min结点的$\alpha 、\beta$，然后继续搜索下一个子节点。
   c. 如果刚好把这个max/min结点的子节点都搜完了，就直接计算max/min结点的值，然后将max/min结点当作一个普通结点，返回他的值，进行下一轮的回溯判断。

3 举例

我知道的，千言万语不如一个题目更让人醍醐灌顶。写个题目，展现下思路吧。
by the way，如果下面步骤有疑惑的，请翻到上文，阅读小节2
如果阅读后还有疑惑，那可能是我错了（orz），请评论区留言。

3.1 题目

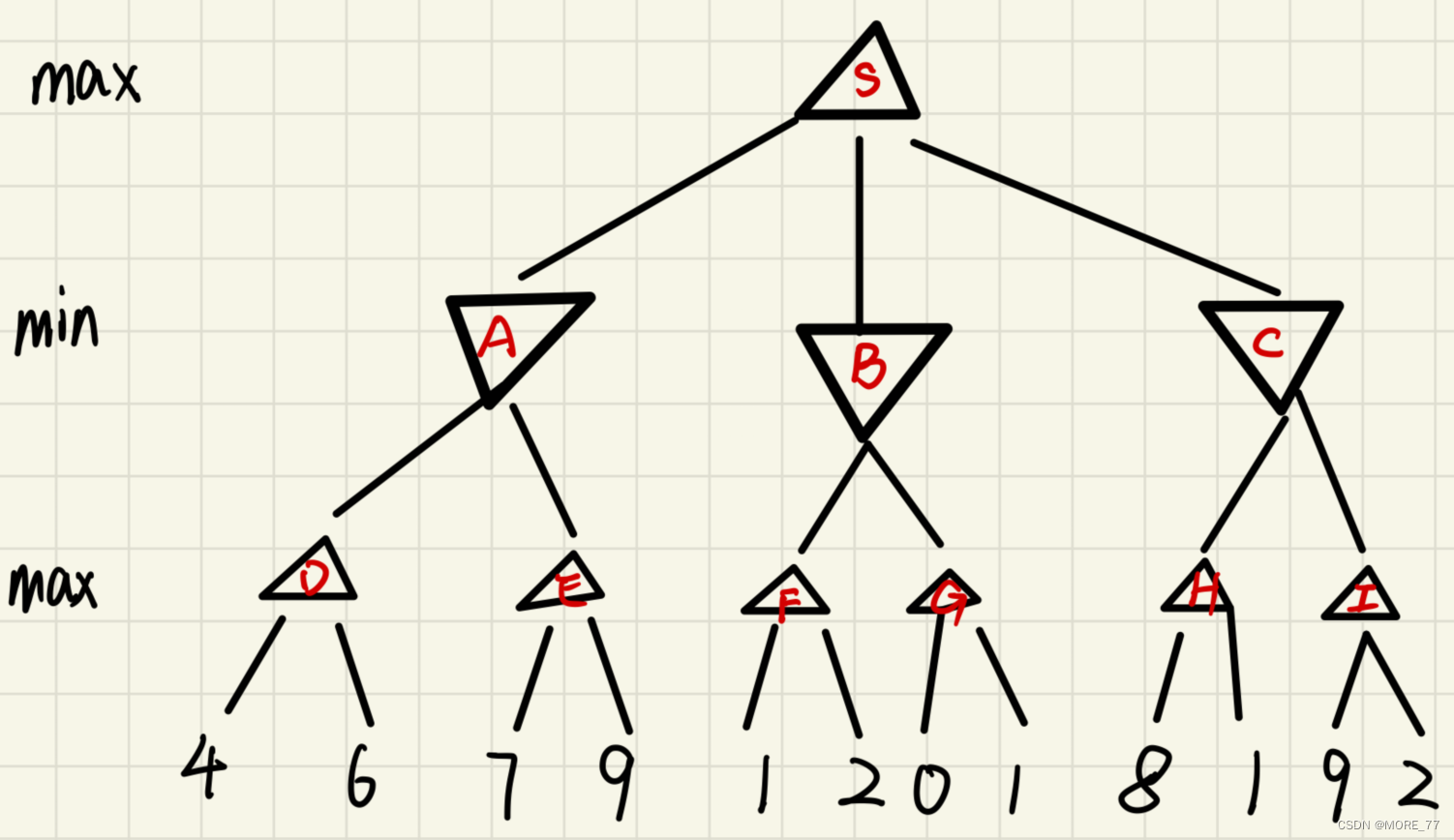
3.2 步骤

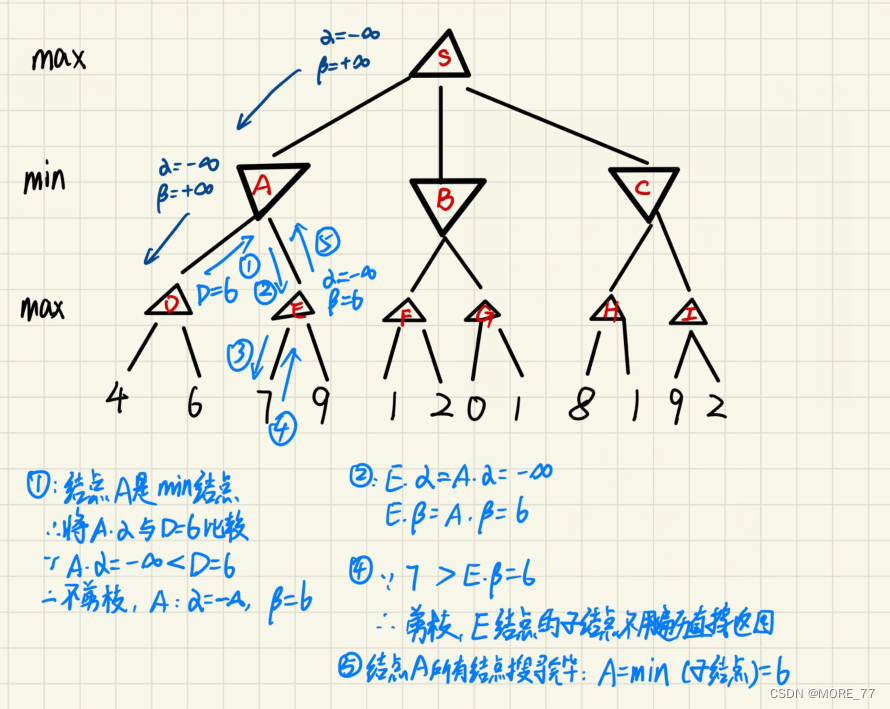
1 搜索完结点D的所有子节点

2 搜索完结点A的所有子节点

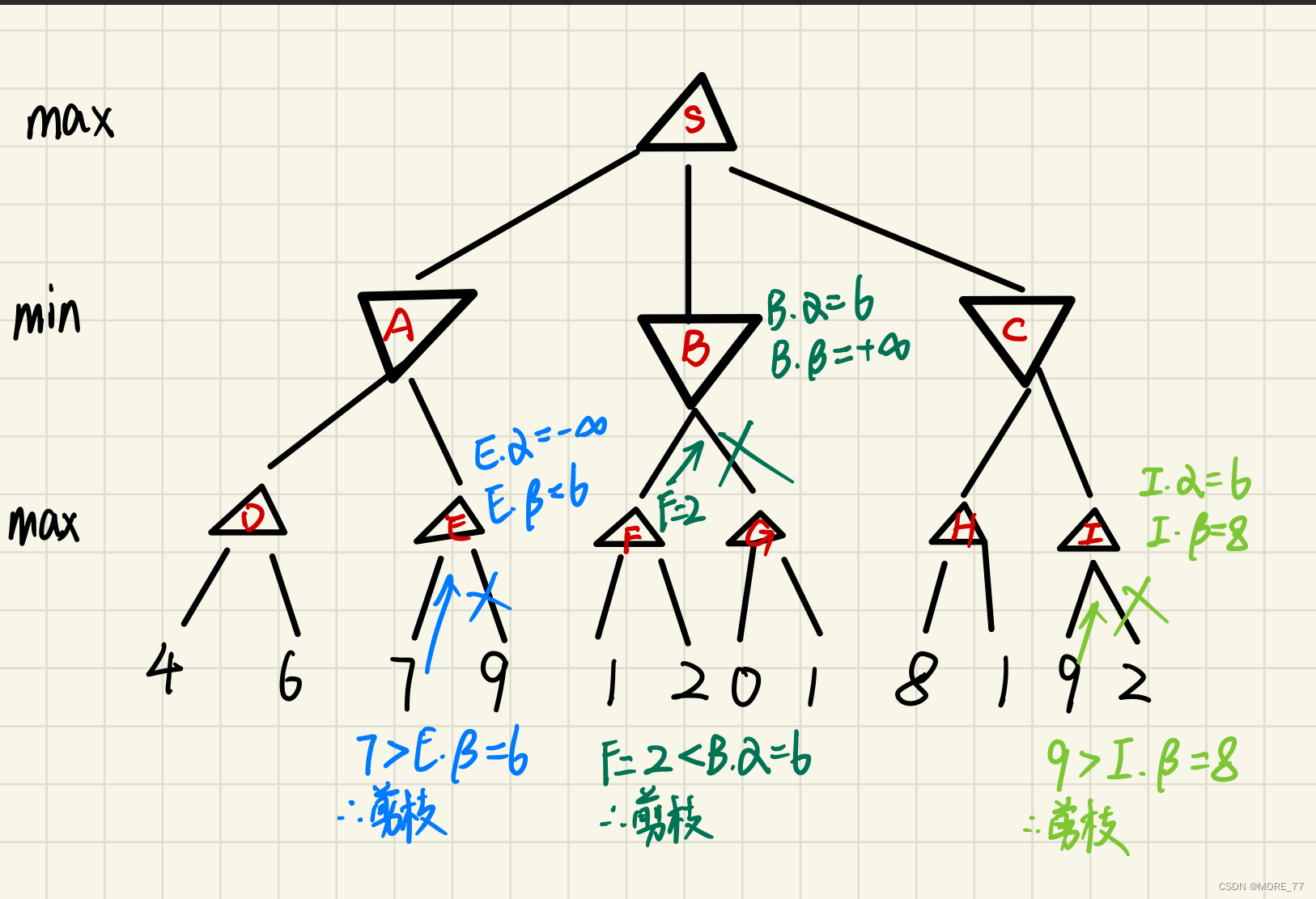
3 搜索完结点C之前的结点

4 全部搜索完

5 答案

4 结尾

太不容易了，画个图，做个题花好多时间啊。
如有帮助，请多多点赞！谢谢！！