前置知识

关于最小生成树

先说「树」和「图」的根本区别：树不会包含环，图可以包含环

树就是「无环连通图」

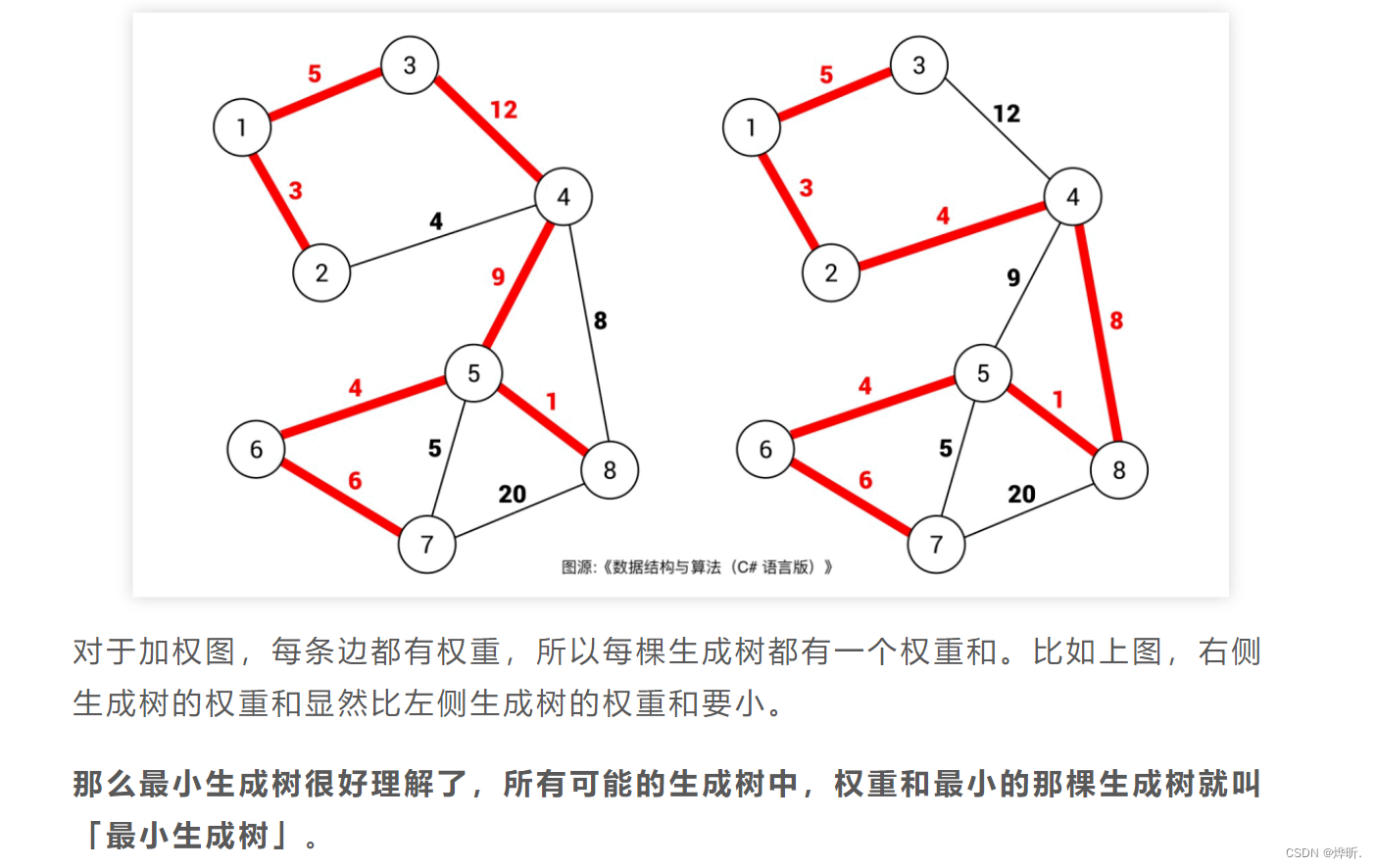
生成树是含有图中所有顶点的「无环连通子图」

你要保证这些边：

1、包含图中的所有节点。

2、形成的结构是树结构（即不存在环）。

3、权重和最小。

关于Union-Find

=> 作用：对树进行判定

对于添加的这条边，如果该边的两个节点本来就在同一连通分量里，那么添加这条边会产生环；

反之，如果该边的两个节点不在同一连通分量里，则添加这条边不会产生环。

判断两个节点是否连通（是否在同一个连通分量中）就是 Union-Find 算法的拿手绝活

同一个连通分量就是有着共同父节点的一群结点

Kruskal算法

Kruskal算法就是在确保一些结点在一些边的关系下能构成树时执行贪心算法

说白了就是按照权重大小就是从小到大进行排序

connections里面的vector的前两项放的是结点，后面放的是权重

#include <bits/stdc++.h>
using namespace std;class UF {
private:int count = 0; // 记录连通分量vector<int> parent; // 节点x的父节点是parent[x]public:UF(int n) {this->count = n;parent.resize(n);for(int i = 0; i < n; i++) {parent[i] = i;}}void Union(int p, int q) {int rootP = find(p);int rootQ = find(q);if(rootP == rootQ) return;parent[rootQ] = rootP;count--;}bool connected(int p, int q) {int rootP = find(p);int rootQ = find(q);return rootP == rootQ;}int find(int x) {// 根节点的parent[x] == x，层层向上找就好啦if(parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}int getCount() { return count; }};int Kruskal(vector<vector<int>>& connections) {int n = connections.size();
//    序号从1 -> nUF uf(n + 1);sort(connections.begin(), connections.end(), [](auto& a, auto& b) { return a[2] < b[2]; });int mst = 0;for(auto c: connections) {int u = c[0], v = c[1], weight = c[2];
//        如果这两个结点是同一连通分量=> 则不能连接if(uf.connected(u, v)) continue;mst += weight;uf.Union(u, v);}
//    0开着没用return uf.getCount() == 2 ? mst : -1;
}int main() {int n;cin >> n;vector<vector<int>> connections;while(n--) {int u, v, weight;cin >> u >> v >> weight;vector<int> temp(3);temp[0] = u, temp[1] = v, temp[2] = weight;connections.emplace_back(temp);}cout << Kruskal(connections);return 0;
}

1584. 连接所有点的最小费用 - 力扣（LeetCode）

class UF {
private:int count = 0;vector<int> parent;public:UF(int n) {this->count = n;parent.resize(n);for(int i = 0; i < n; i++) parent[i] = i;}void Union(int p, int q) {int rootP = find(p), rootQ = find(q);if(rootP == rootQ) return;parent[rootQ] = rootP;count--;}bool connected(int p, int q) {int rootP = find(p), rootQ = find(q);return rootP == rootQ;}int find(int x) {if(parent[x] != x) parent[x] = find(parent[x]);return parent[x];}int getCount() { return count; }
};class Solution {
public:int minCostConnectPoints(vector<vector<int>>& points) {// 这题要根据给的points先构造一个connectionsvector<vector<int>> connections;int n = points.size();for(int i = 0; i < n; i++) {for(int j = i + 1; j < n ; j++) {int xi = points[i][0], yi = points[i][1];int xj = points[j][0], yj = points[j][1];connections.push_back({i, j, abs(xi - xj) + abs(yi - yj)});}}// &不加是拷贝，会增加时间复杂度sort(connections.begin(), connections.end(), [](auto& a, auto& b){ return a[2] < b[2]; });int mst = 0;UF uf(n);for(auto& c: connections) {int u = c[0], v = c[1], weight = c[2];if(uf.connected(u, v)) continue;mst += weight;uf.Union(u, v);}return uf.getCount() == 1 ? mst : -1;}};