算法小课堂(六)回溯算法
%e5%9b%9e%e6%ba%af%e7%ae%97%e6%b3%95.jpg)
目录
一、概述
1.1概念(树形结构)
1.2区别
1.3步骤
1.4回溯法模板
1.5应用
1.6回溯三部曲
二、组合问题
2.1组合
回溯算法
优化剪枝操作
2.2组合总和
2.3组合总和2
2.4组合总和3
2.5电话号码的字母组合
三、切割问题
3.1分割回文串
3.2.复原IP地址
四、子集问题
4.1子集
4.2子集2
4.3递增子序列
五、排列问题
5.1全排列
5.2全排列 II
六、棋盘问题
6.1N皇后
6.2解数独
7.1 0-1背包(子集问题)
7.2旅行售货员问题
7.3装载问题(组合问题)
7.4图的着色问题(组合问题)
7.5最大团问题
一、概述
1.1概念(树形结构)
回溯算法是一种系统地搜索问题的解的方法。某个问题的所有可能解的称为问题的解空间,若解空间是有限的,则可将解空间映射成树结构。回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
回溯是递归的副产品,只要有递归就会有回溯。
回溯法就是暴力搜索,并不是什么高效的算法,最多在剪枝一下。
1.2区别
回溯算法和深度优先搜索(DFS)有很多相似之处,但也有不同之处。回溯算法在搜索过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。而DFS则是在搜索过程中遍历所有可能的路径,直到找到问题的解
1.3步骤
- 状态表示:需要定义状态表示方式,以便在搜索过程中能够正确地扩展状态。
- 决策生成:需要确定当前状态下的所有可能决策,以便进行进一步的搜索。
- 解空间剪枝:需要根据问题的特点,对搜索过程中无用的状态进行剪枝,以提高算法效率。
- 解的输出:需要根据问题的要求,确定如何输出符合要求的解。
1.4回溯法模板
result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择其中,
result存储结果,backtrack是回溯函数,路径是已经做出的选择,选择列表是当前可以做出的选择。
1.5应用
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等。
1.6回溯三部曲
回溯算法三部曲是指:1. 确定递归函数的参数和返回值;2. 确定终止条件;3. 确定单层搜索的过程。 回溯算法是一种暴力搜索算法,它通过不断地尝试所有可能的结果来解决问题。在回溯算法中,我们需要对每个可能的结果进行判断,如果符合条件就加入到结果集中,否则就回溯到上一步,继续尝试其他可能的结果。
二、组合问题
2.1组合
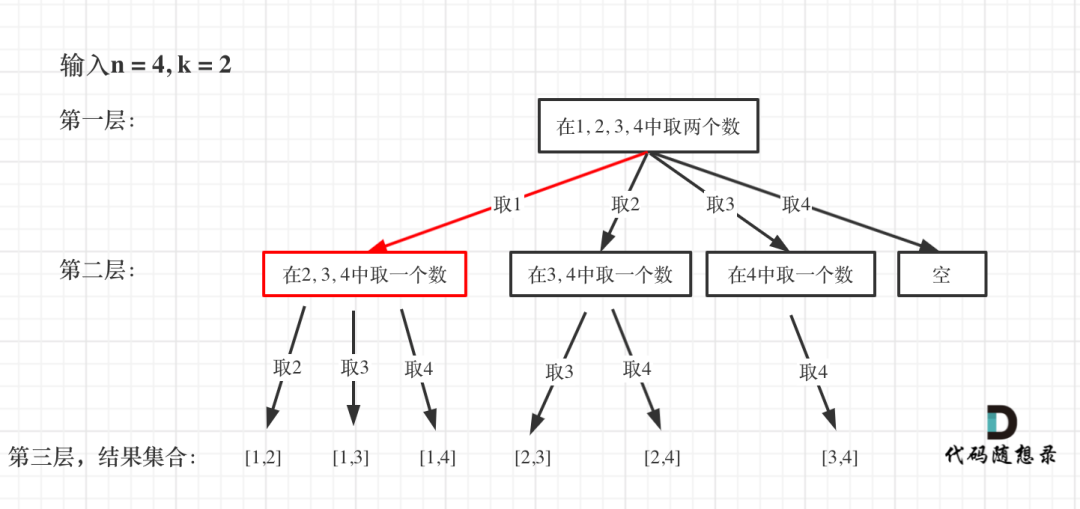
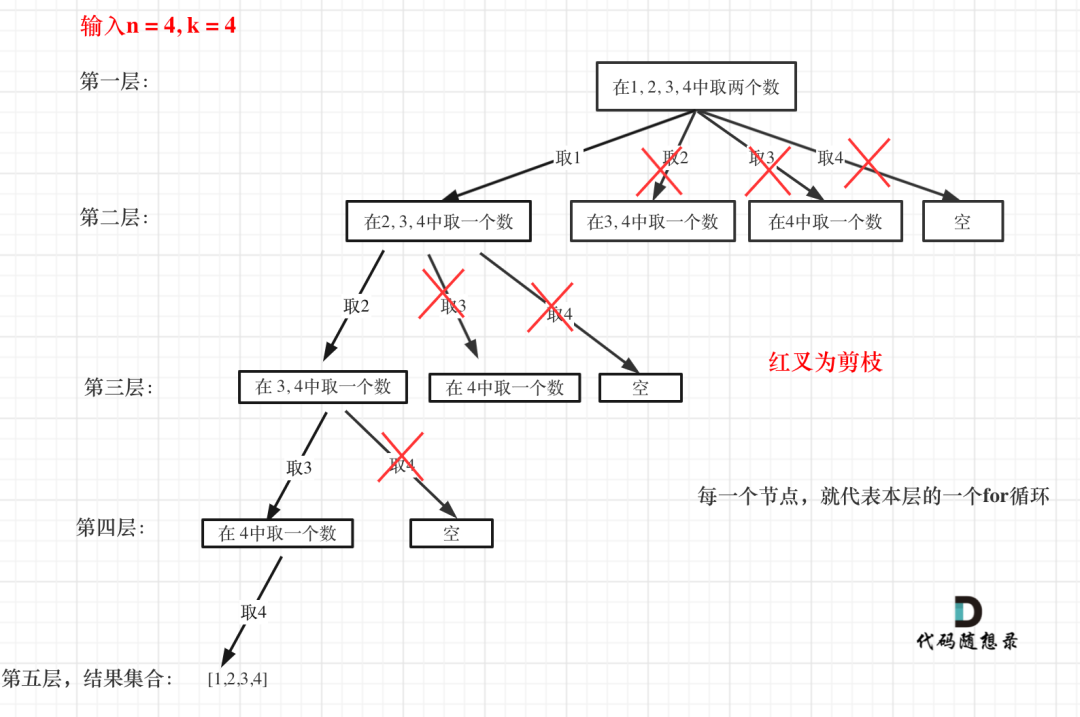
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
#include<stdio.h>
#include <iostream>using namespace std;const int N = 100;
int a[N];
int n, k;
void dfs(int cur, int cnt) {if (cnt == k) {for (int i = 0; i < k; i++) {cout << a[i] << " ";}cout << endl;return;}for (int i = cur; i <= n; i++) {a[cnt] = i;dfs(i + 1, cnt + 1);}
}
int main() {cin >> n >> k;dfs(1, 0);return 0;
}
回溯算法
import java.util.*;public class Solution {// 回溯函数private void backtracking(List<List<Integer>> result, List<Integer> path, int n, int k, int startIndex) {if (path.size() == k) { // 如果path中的元素个数等于k,说明找到了一组符合条件的组合result.add(new ArrayList<>(path)); // 将该组合加入结果集中return; // 返回上一层递归}// 枚举所有可能的数for (int i = startIndex; i <= n; i++) {path.add(i); // 将当前数加入path中,进行处理backtracking(result, path, n, k, i + 1); // 递归处理下一个数path.remove(path.size() - 1); // 撤销处理的数,回溯到上一层状态}}// 组合函数public List<List<Integer>> combine(int n, int k) {List<List<Integer>> result = new ArrayList<>(); // 存储符合条件的结果集List<Integer> path = new ArrayList<>(); // 存储符合条件的组合backtracking(result, path, n, k, 1); // 开始回溯,从数字1开始return result; // 返回结果集}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 获取用户输入的nint k = scanner.nextInt(); // 获取用户输入的kscanner.close(); // 关闭ScannerSolution solution = new Solution(); // 创建Solution对象List<List<Integer>> result = solution.combine(n, k); // 调用组合函数,得到符合条件的结果集for (List<Integer> list : result) { // 遍历结果集for (int num : list) { // 遍历组合System.out.print(num + " "); // 输出组合中的元素}System.out.println(); // 输出换行,用于分隔每个组合}}
}
优化剪枝操作
剪枝操作是回溯算法的一种优化方法,可以排除不满足解的情况来提高算法的执行效率。在回溯算法中,剪枝操作可以有多种方式,例如对for循环选择的起始范围的剪枝,或者在递归过程中判断是否需要继续递归等等
import java.util.*;public class Solution {// 回溯函数private void backtracking(List<List<Integer>> result, List<Integer> path, int n, int k, int startIndex) {if (path.size() == k) { // 如果path中的元素个数等于k,说明找到了一组符合条件的组合result.add(new ArrayList<>(path)); // 将该组合加入结果集中return; // 返回上一层递归}// 枚举所有可能的数for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {//优化的地方path.add(i); // 将当前数加入path中,进行处理backtracking(result, path, n, k, i + 1); // 递归处理下一个数path.remove(path.size() - 1); // 撤销处理的数,回溯到上一层状态}}// 组合函数public List<List<Integer>> combine(int n, int k) {List<List<Integer>> result = new ArrayList<>(); // 存储符合条件的结果集List<Integer> path = new ArrayList<>(); // 存储符合条件的组合backtracking(result, path, n, k, 1); // 开始回溯,从数字1开始return result; // 返回结果集}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 获取用户输入的nint k = scanner.nextInt(); // 获取用户输入的kscanner.close(); // 关闭ScannerSolution solution = new Solution(); // 创建Solution对象List<List<Integer>> result = solution.combine(n, k); // 调用组合函数,得到符合条件的结果集for (List<Integer> list : result) { // 遍历结果集for (int num : list) { // 遍历组合System.out.print(num + " "); // 输出组合中的元素}System.out.println(); // 输出换行,用于分隔每个组合}}
}
2.2组合总和
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
思路
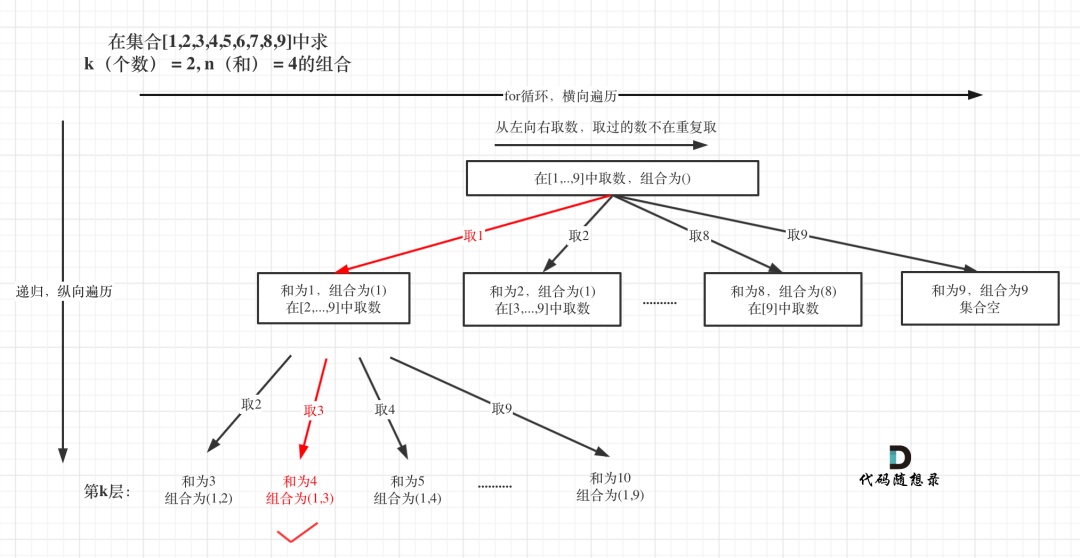
本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。
相对于上题,无非就是多了一个限制,本题是要找到和为n的k个数的组合,而整个集合已经是固定的了[1,...,9]。
例如 k = 2,n = 4的话,就是在集合[1,2,3,4,5,6,7,8,9]中求 k(个数) = 2, n(和) = 4的组合。
import java.util.*;class Solution {private List<List<Integer>> result; // 存放结果集private List<Integer> path; // 符合条件的结果/* backtracking - 回溯算法 @param targetSum 目标和,也就是题目中的n。* @param k 题目中要求k个数的集合。* @param sum 已经收集的元素的总和,也就是path里元素的总和。* @param startIndex 下一层for循环搜索的起始位置。*/private void backtracking(int targetSum, int k, int sum, int startIndex) {// 剪枝操作:如果path里的元素个数已经等于k,且当前元素总和不等于目标和targetSum,直接返回。if (path.size() == k && sum != targetSum) {return;}// 如果path里的元素个数已经等于k,且当前元素总和等于目标和targetSum,说明已经找到了符合条件的结果,加入到结果集中并返回。if (path.size() == k && sum == targetSum) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= 9; i++) {sum += i; // 处理path.add(i); // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯path.remove(path.size() - 1); // 回溯}}public List<List<Integer>> combinationSum3(int k, int n) {result = new ArrayList<>();path = new ArrayList<>();backtracking(n, k, 0, 1);return result;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int k = scanner.nextInt(); // 读取sinint n = scanner.nextInt(); // 读取nSolution solution = new Solution();List<List<Integer>> result = solution.combinationSum3(k, n);System.out.println(result);}
}
2.3组合总和2
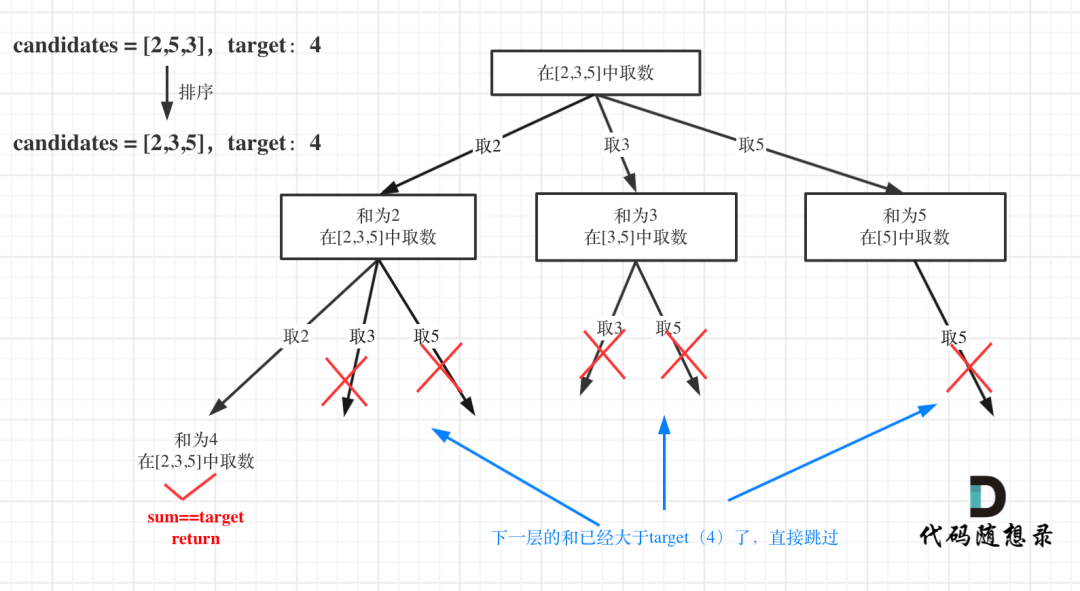
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:输入:candidates = [2,3,6,7], target = 7, 所求解集为:[ [7], [2,2,3] ]
提示
组合没有数量要求
元素可无限重复选
import java.util.*;class Solution {public List<List<Integer>> combinationSum(int[] candidates, int target) {List<List<Integer>> res = new ArrayList<>();Arrays.sort(candidates); // 先进行排序backtracking(res, new ArrayList<>(), candidates, target, 0, 0);return res;}public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {// 找到了数字和为 target 的组合if (sum == target) {res.add(new ArrayList<>(path));return;}for (int i = idx; i < candidates.length; i++) {// 如果 sum + candidates[i] > target 就终止遍历if (sum + candidates[i] > target) break;path.add(candidates[i]);backtracking(res, path, candidates, target, sum + candidates[i], i);path.remove(path.size() - 1); // 回溯,移除路径 path 最后一个元素}}public static void main(String[] args) {Solution s = new Solution();int[] candidates1 = {2, 3, 6, 7};int target1 = 7;List<List<Integer>> res1 = s.combinationSum(candidates1, target1);System.out.println(res1); // [[7], [2, 2, 3]]int[] candidates2 = {2, 3, 5};int target2 = 8;List<List<Integer>> res2 = s.combinationSum(candidates2, target2);System.out.println(res2); // [[2, 2, 2, 2], [2, 3, 3], [3, 5]]}
}
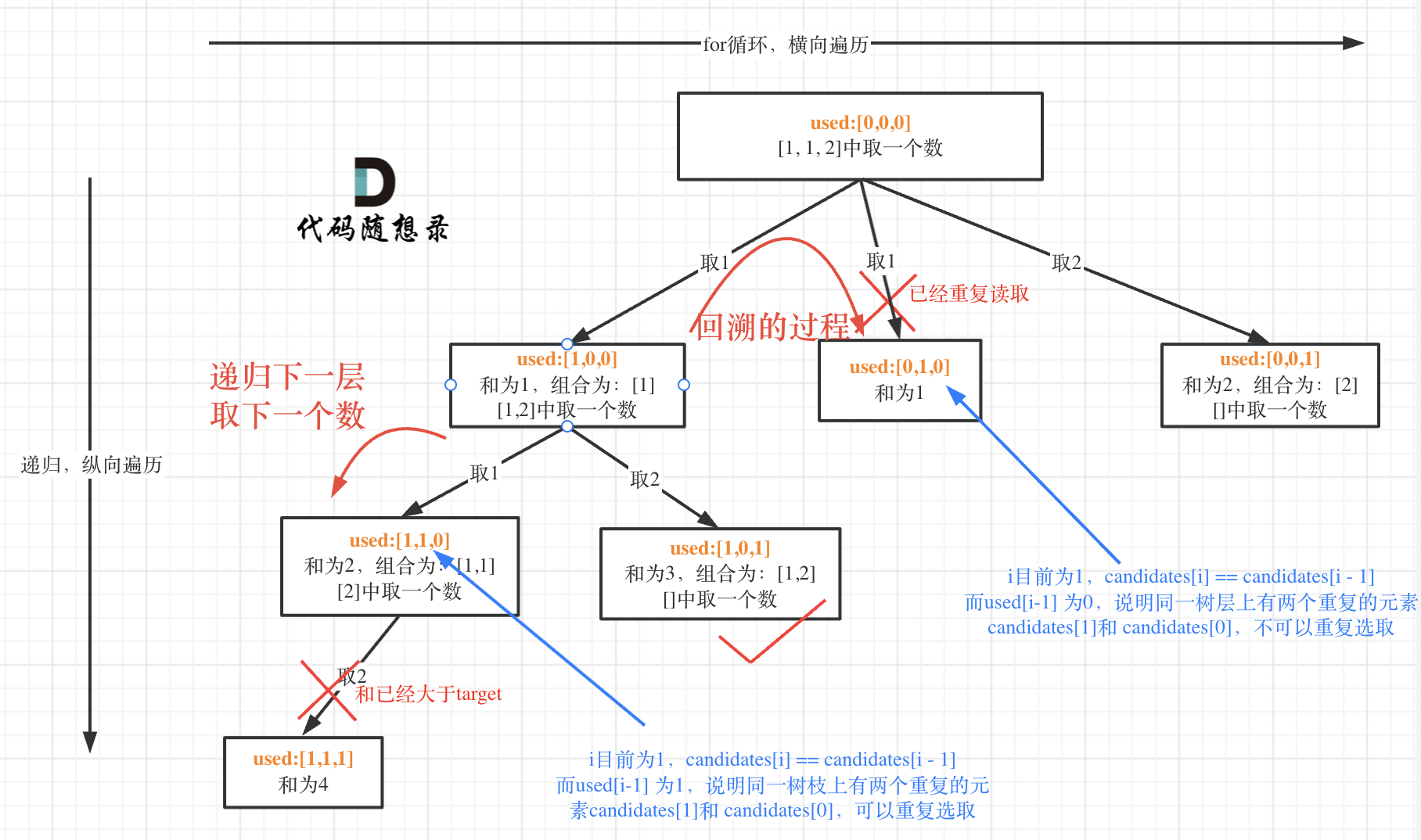
2.4组合总和3
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
- 示例 1:
- 输入: candidates = [10,1,2,7,6,1,5], target = 8,
- 所求解集为:
[[1, 7],[1, 2, 5],[2, 6],[1, 1, 6] ]
思路
- 本题candidates 中的每个数字在每个组合中只能使用一次。
- 本题数组candidates的元素是有重复的
import java.util.*;class Solution {LinkedList<Integer> path = new LinkedList<>();List<List<Integer>> ans = new ArrayList<>();boolean[] used;int sum = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {used = new boolean[candidates.length];// 加标志数组,用来辅助判断同层节点是否已经遍历Arrays.fill(used, false);// 为了将重复的数字都放到一起,所以先进行排序Arrays.sort(candidates);backTracking(candidates, target, 0);return ans;}private void backTracking(int[] candidates, int target, int startIndex) {if (sum == target) {ans.add(new ArrayList(path));}for (int i = startIndex; i < candidates.length; i++) {if (sum + candidates[i] > target) {break;}// 出现重复节点,同层的第一个节点已经被访问过,所以直接跳过if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {continue;}used[i] = true;sum += candidates[i];path.add(candidates[i]);// 每个节点仅能选择一次,所以从下一位开始backTracking(candidates, target, i + 1);used[i] = false;sum -= candidates[i];path.removeLast();}}public static void main(String[] args) {Solution s = new Solution();int[] candidates = {10, 1, 2, 7, 6, 1, 5};int target = 8;List<List<Integer>> result = s.combinationSum2(candidates, target);System.out.println(result); // expected: [[1, 1, 6], [1, 2, 5], [1, 7], [2, 6]]}
}
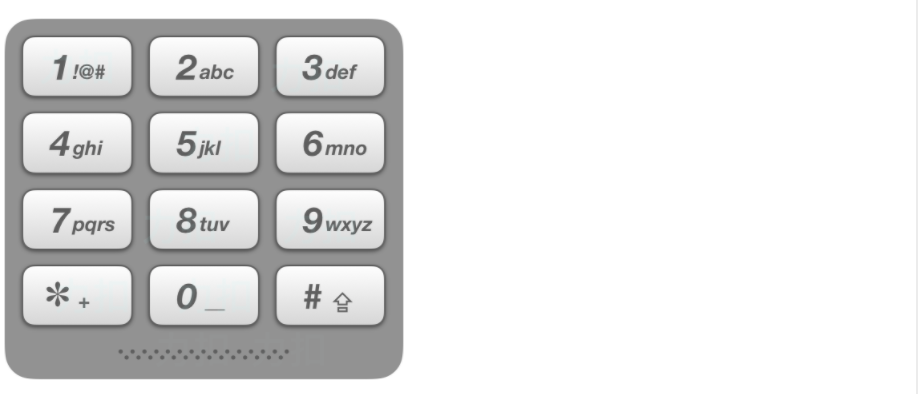
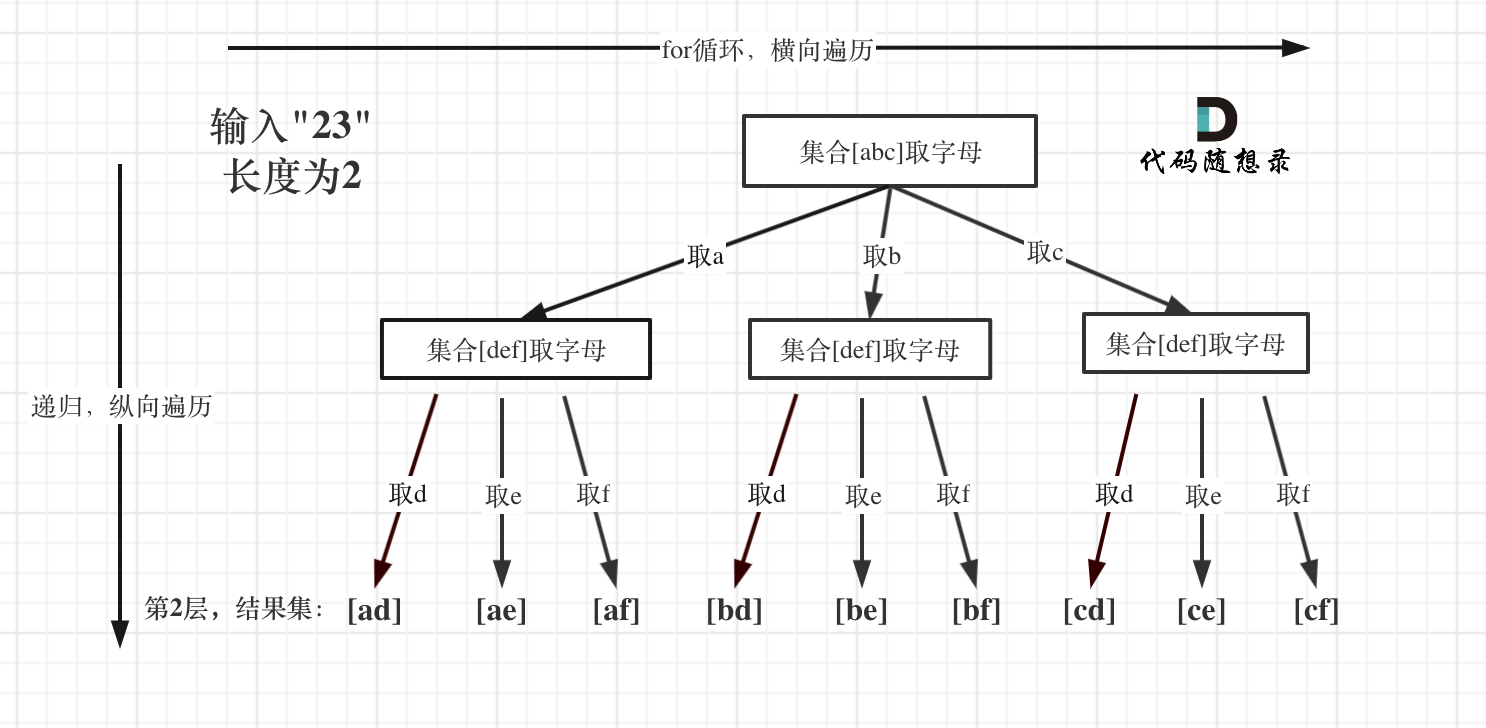
2.5电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例:
- 输入:"23"
- 输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
import java.util.*;class Solution {// 字母映射表private final String[] letterMap = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz" // 9};private List<String> result = new ArrayList<>(); // 存储所有结果private StringBuilder s = new StringBuilder(); // 存储每个组合private void backtracking(String digits, int index) {if (index == digits.length()) { // 当处理到最后一个数字时,将s加入result中result.add(s.toString());return;}int digit = digits.charAt(index) - '0'; // 将当前数字转为intString letters = letterMap[digit]; // 找出数字对应的字符集for (int i = 0; i < letters.length(); i++) {s.append(letters.charAt(i)); // 将当前字符加入sbacktracking(digits, index + 1); // 递归到下一个数字s.deleteCharAt(s.length() - 1); // 回溯,将最后一个字符删除}}public List<String> letterCombinations(String digits) {result.clear(); // 清空results.setLength(0); // 清空sif (digits.length() == 0) { // 边界条件,当输入为空时,直接返回resultreturn result;}backtracking(digits, 0); // 从第一个数字开始处理return result;}}public class Main {public static void main(String[] args) {Solution sol = new Solution();String digits1 = "23";List<String> res1 = sol.letterCombinations(digits1);System.out.println(res1);String digits2 = "";List<String> res2 = sol.letterCombinations(digits2);System.out.println(res2);String digits3 = "2";List<String> res3 = sol.letterCombinations(digits3);System.out.println(res3);}
}三、切割问题
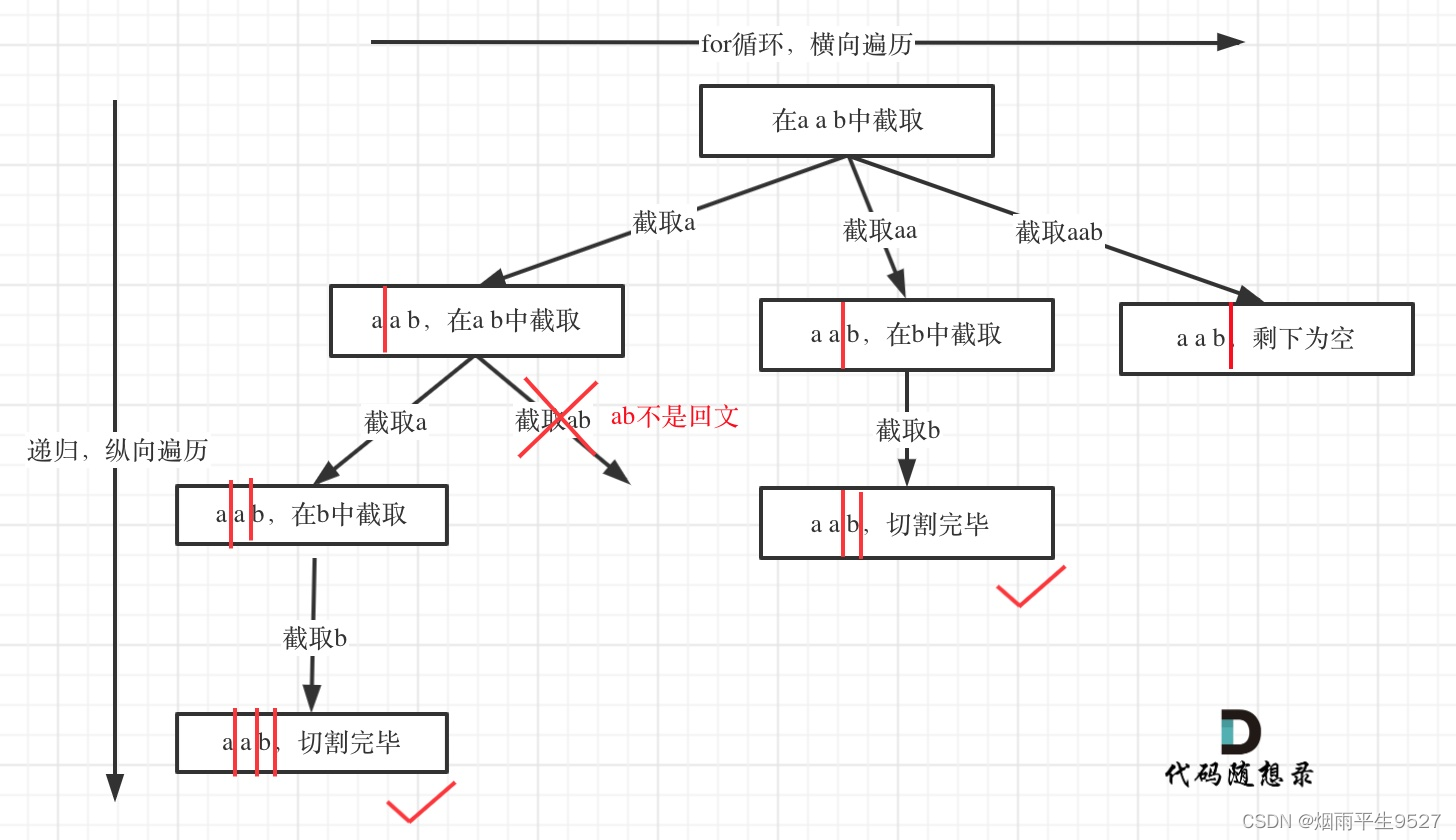
3.1分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]
思路
- 切割问题,有不同的切割方式
- 判断回文
import java.util.*;class Solution {private List<List<String>> result = new ArrayList<>();private List<String> path = new ArrayList<>(); // 存放已经回文的子串private void backtracking(String s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.length()) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i < s.length(); i++) {if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串String str = s.substring(startIndex, i + 1);path.add(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.remove(path.size() - 1); // 回溯过程,弹出本次已经填在的子串}}private boolean isPalindrome(String s, int start, int end) {// 判断从start到end的子串是否是回文子串while (start < end) {if (s.charAt(start++) != s.charAt(end--)) {return false;}}return true;}public List<List<String>> partition(String s) {result.clear();path.clear();backtracking(s, 0);return result;}
}
public class Main {public static void main(String[] args) {Solution sol = new Solution();List<List<String>> res1 = sol.partition("aab");System.out.println(res1);List<List<String>> res2 = sol.partition("a");System.out.println(res2);List<List<String>> res3 = sol.partition("racecar");System.out.println(res3);}
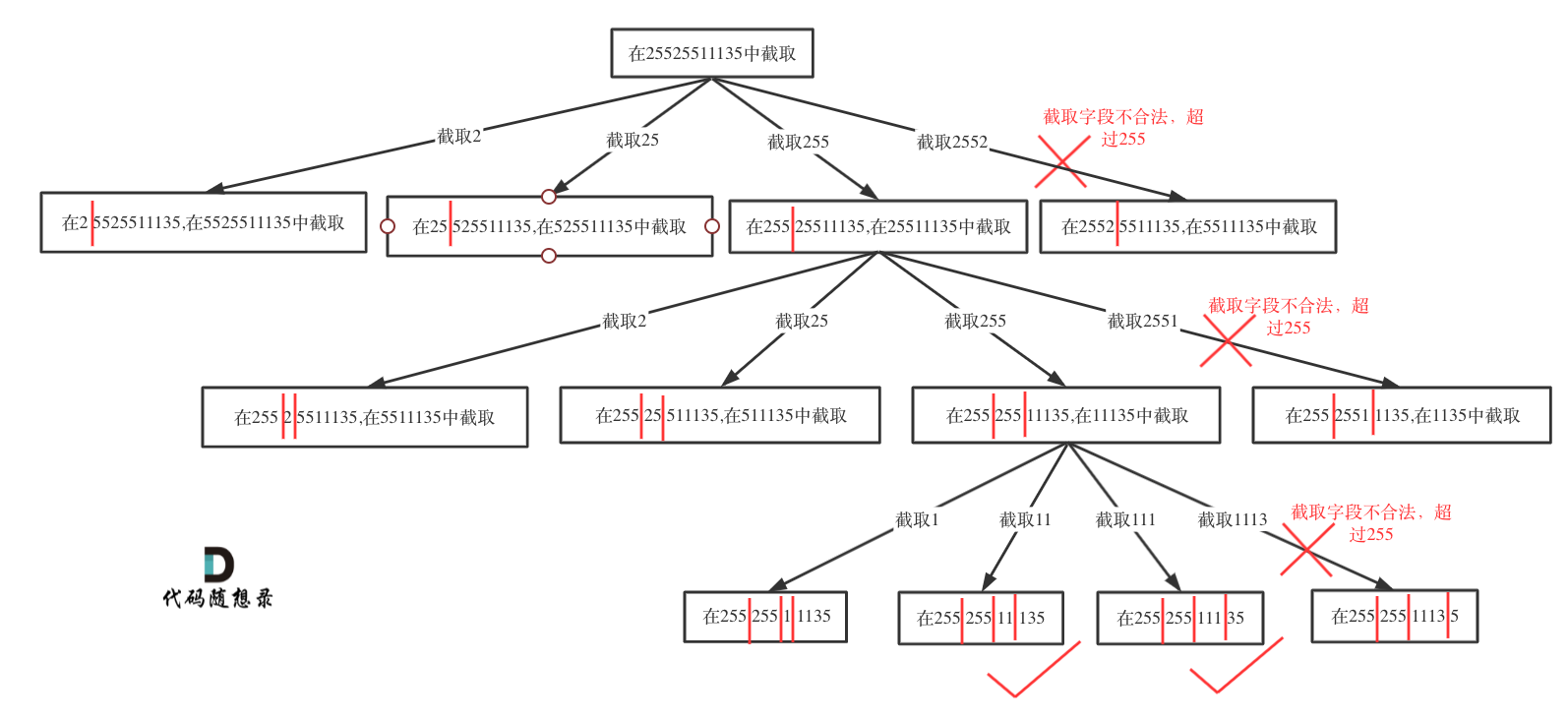
}3.2.复原IP地址
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效的 IP 地址。
示例 1:
- 输入:s = "25525511135"
- 输出:["255.255.11.135","255.255.111.35"]
示例 2:
- 输入:s = "0000"
- 输出:["0.0.0.0"]
提示
切割问题就可以使用回溯搜索法把所有可能性搜出来
import java.util.*;class Solution {private List<String> result = new ArrayList<>(); // 记录结果// startIndex: 搜索的起始位置,pointNum:添加逗点的数量private void backtracking(String s, int startIndex, int pointNum) {if (pointNum == 3) { // 逗点数量为3时,分隔结束// 判断第四段子字符串是否合法,如果合法就放进result中if (isValid(s, startIndex, s.length() - 1)) {result.add(s);}return;}for (int i = startIndex; i < s.length(); i++) {if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法s = s.substring(0, i + 1) + "." + s.substring(i + 1); // 在i的后面插入一个逗点pointNum++;backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2pointNum--; // 回溯s = s.substring(0, i + 1) + s.substring(i + 2); // 回溯删掉逗点} else {break; // 不合法,直接结束本层循环}}}// 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法private boolean isValid(String s, int start, int end) {if (start > end) {return false;}if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法return false;}int num = 0;for (int i = start; i <= end; i++) {if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到非数字字符不合法return false;}num = num * 10 + (s.charAt(i) - '0');if (num > 255) { // 如果大于255了不合法return false;}}return true;}public List<String> restoreIpAddresses(String s) {result.clear();if (s.length() < 4 || s.length() > 12) {return result; // 算是剪枝了}backtracking(s, 0, 0);return result;}public static void main(String[] args) {Solution solution = new Solution();List<String> result = solution.restoreIpAddresses("25525511135");System.out.println(result); // ["255.255.11.135", "255.255.111.35"]}
}四、子集问题
4.1子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
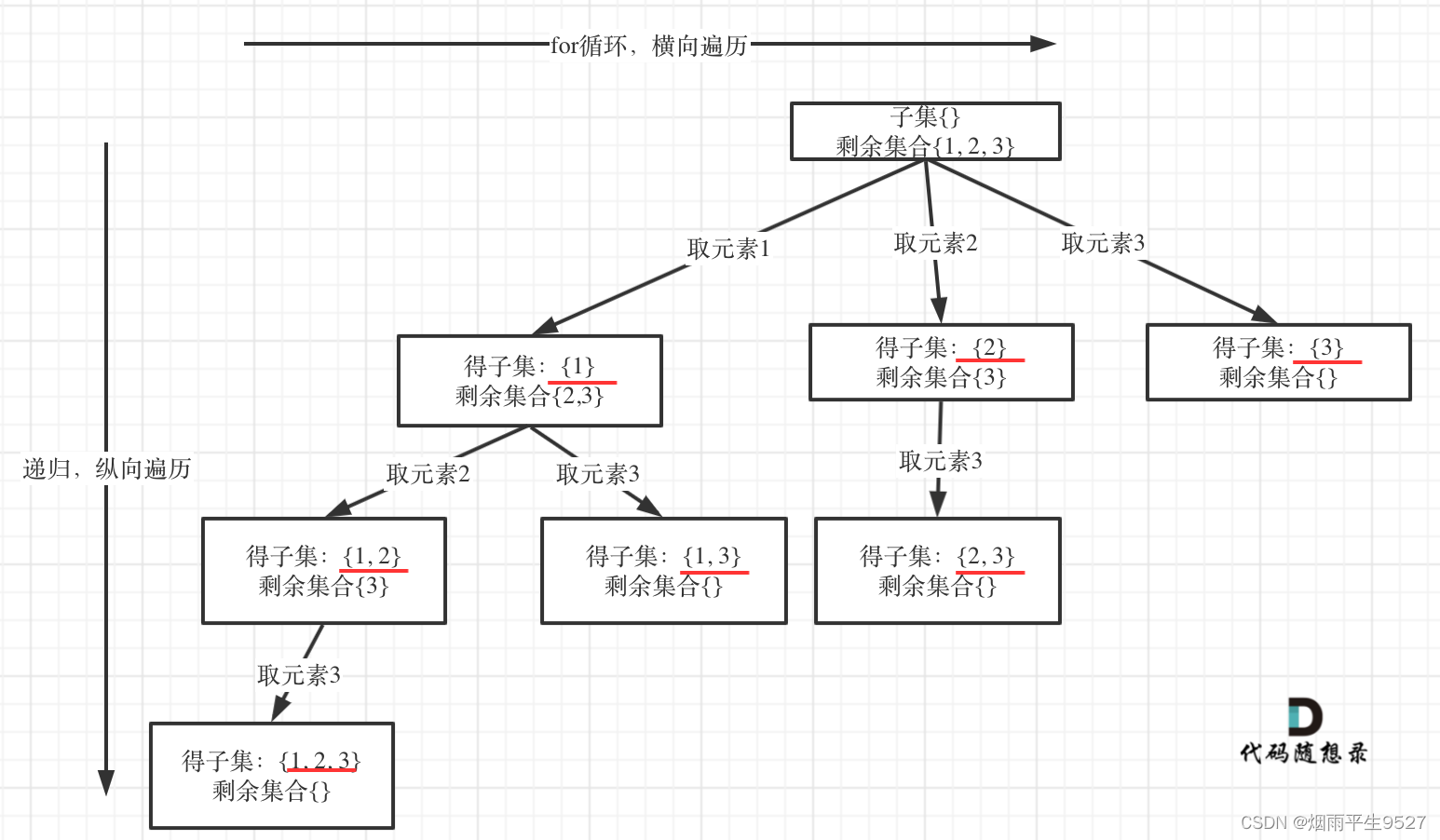
import java.util.ArrayList;
import java.util.List;class Solution {List<List<Integer>> result = new ArrayList<>(); // 存储所有的子集List<Integer> path = new ArrayList<>(); // 存储当前正在生成的子集public List<List<Integer>> subsets(int[] nums) {result.clear();path.clear();backtracking(nums, 0);return result;}private void backtracking(int[] nums, int startIndex) {result.add(new ArrayList<>(path)); // 加入当前生成的子集if (startIndex == nums.length) { // 终止条件return;}for (int i = startIndex; i < nums.length; i++) {path.add(nums[i]);backtracking(nums, i + 1); // 从i+1开始搜索,避免重复path.remove(path.size() - 1); // 回溯}}public static void main(String[] args) {Solution solution = new Solution();int[] nums = {1, 2, 3};List<List<Integer>> subsets = solution.subsets(nums);for (List<Integer> subset : subsets) {System.out.println(subset);}}
}
4.2子集2
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
- 输入: [1,2,2]
- 输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]
思路
集合里有重复元素了,而且求取的子集要去重。
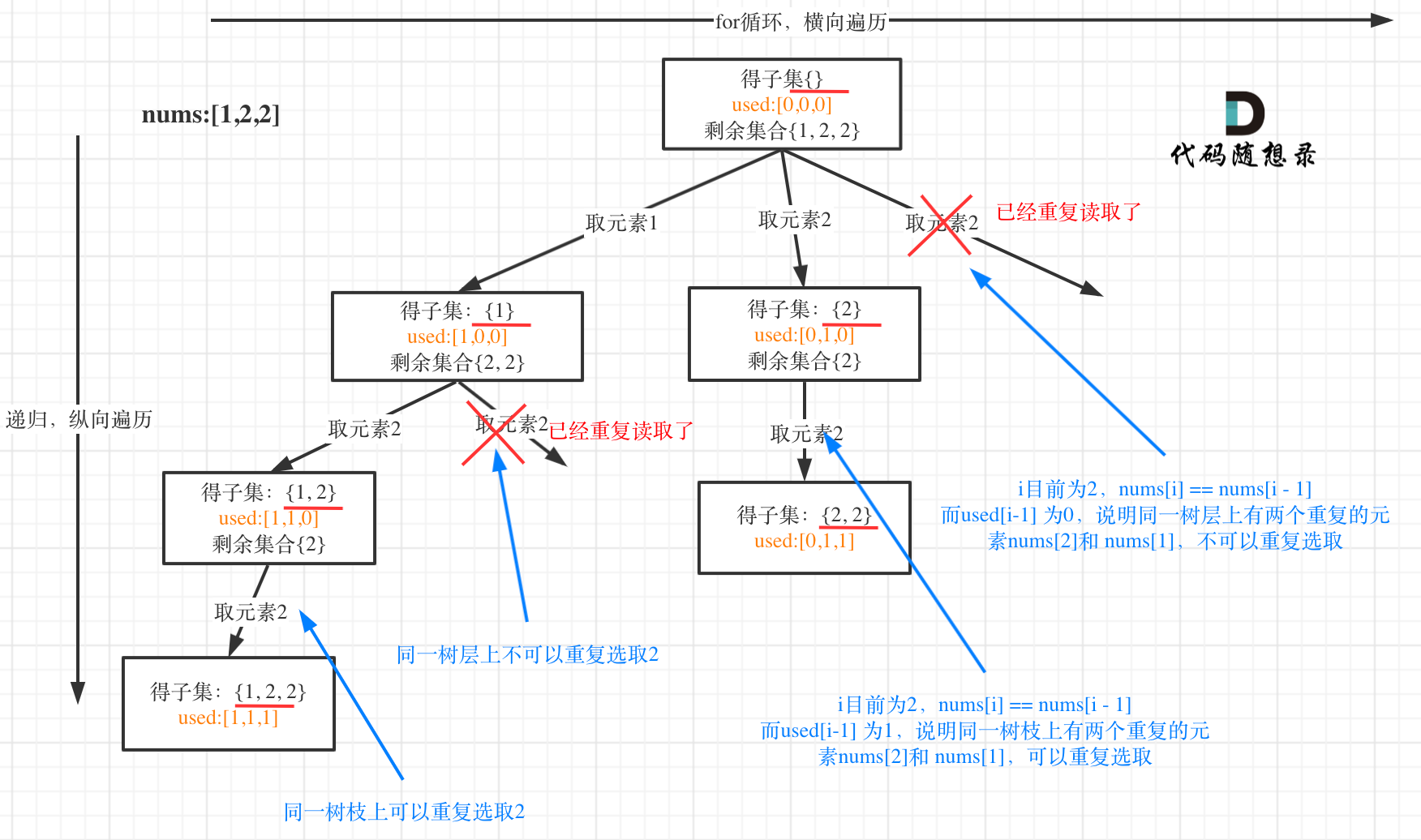
import java.util.*;class Solution {private List<List<Integer>> result;private List<Integer> path;private void backtracking(int[] nums, int startIndex) {result.add(new ArrayList<>(path)); // 收集子集for (int i = startIndex; i < nums.length; i++) {// 如果这个元素和上一个元素一样,并且上一个元素没有被选中,那么这个元素也不用选if (i > startIndex && nums[i] == nums[i - 1]) {continue;}path.add(nums[i]);backtracking(nums, i + 1);path.remove(path.size() - 1);}}public List<List<Integer>> subsetsWithDup(int[] nums) {result = new ArrayList<>();path = new ArrayList<>();Arrays.sort(nums); // 数组排序backtracking(nums, 0);return result;}public static void main(String[] args) {Solution solution = new Solution();int[] nums = {1, 2, 2};List<List<Integer>> subsets = solution.subsetsWithDup(nums);for (List<Integer> subset : subsets) {System.out.println(subset.toString());}}
}
4.3递增子序列
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
- 输入: [4, 6, 7, 7]
- 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
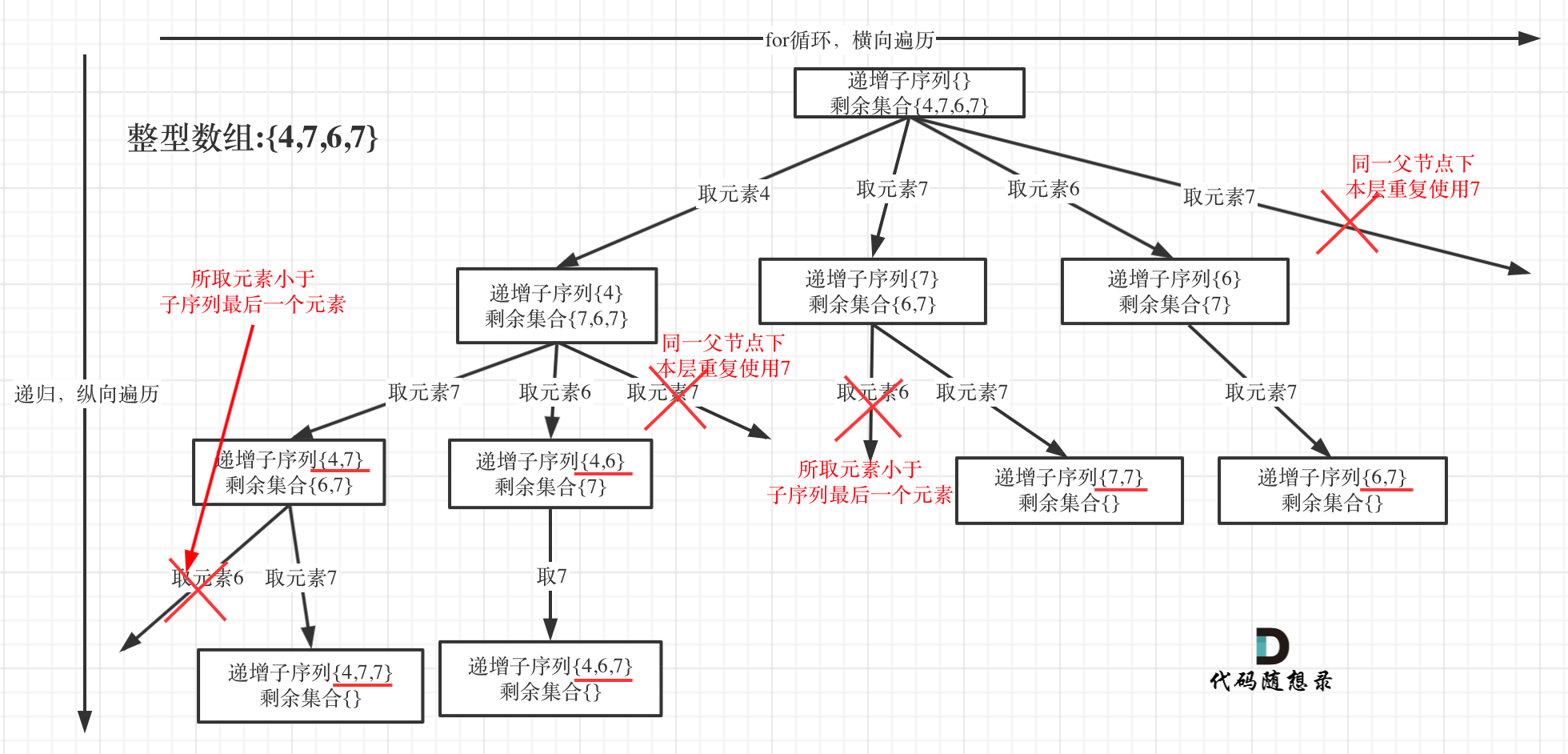
import java.util.*;class Solution {private List<List<Integer>> result = new ArrayList<>();private List<Integer> path = new ArrayList<>();private void backtracking(int[] nums, int startIndex) {if (path.size() > 1) {result.add(new ArrayList<>(path)); // 注意这里要new一个新的list// 注意这里不要加return,要取树上的节点}Set<Integer> set = new HashSet<>(); // 使用set对本层元素进行去重for (int i = startIndex; i < nums.length; i++) {if ((!path.isEmpty() && nums[i] < path.get(path.size() - 1))|| set.contains(nums[i])) {continue;}set.add(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了path.add(nums[i]);backtracking(nums, i + 1);path.remove(path.size() - 1);}}public List<List<Integer>> findSubsequences(int[] nums) {result.clear();path.clear();backtracking(nums, 0);return result;}public static void main(String[] args) {Solution solution = new Solution();int[] nums = {4, 6, 7, 7};List<List<Integer>> result = solution.findSubsequences(nums);System.out.println(result);}
}
五、排列问题
5.1全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
- 输入: [1,2,3]
- 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
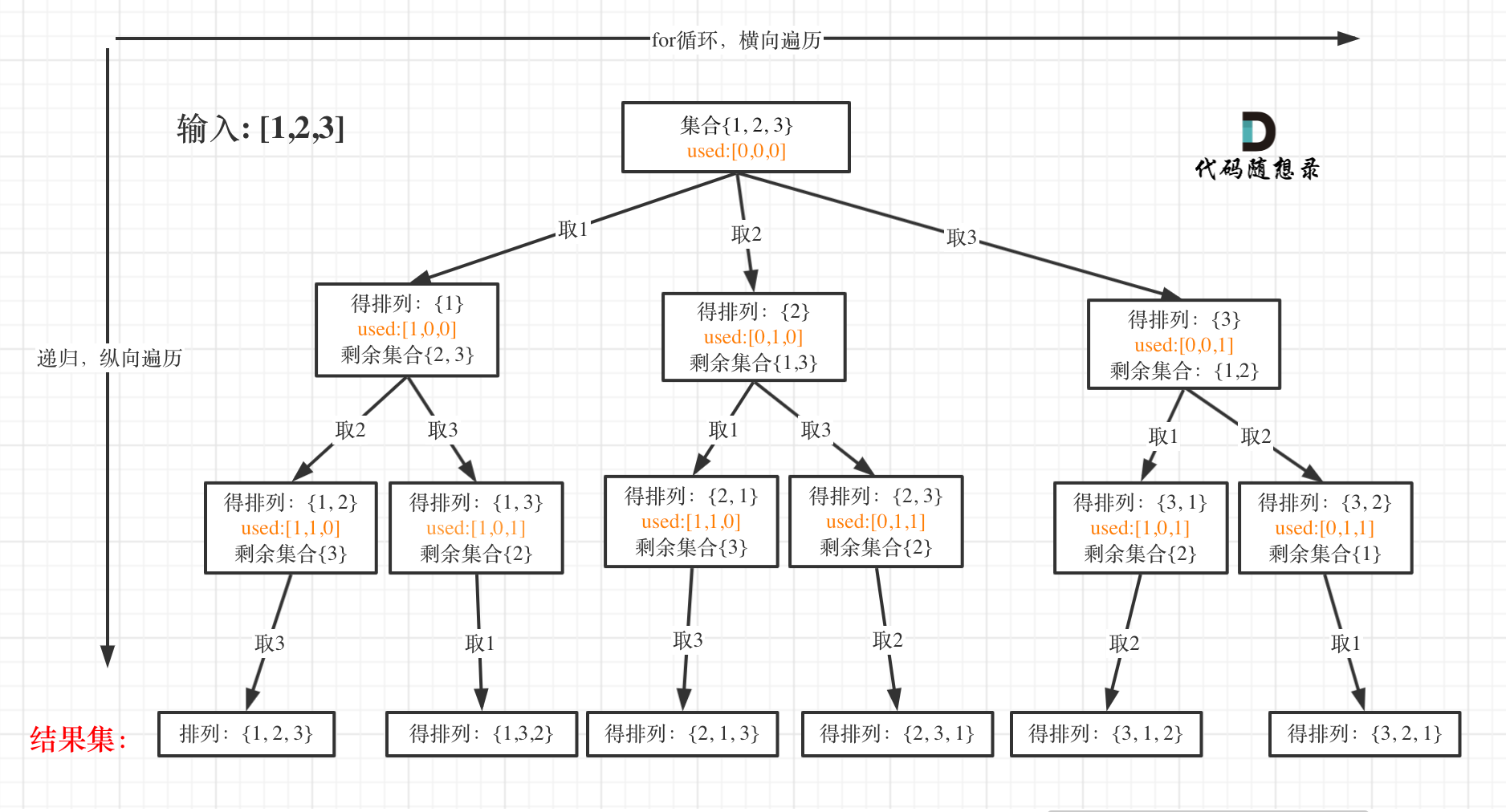
import java.util.*;class Solution {public List<List<Integer>> result = new ArrayList<>();public List<Integer> path = new ArrayList<>();// 回溯算法public void backtracking(List<Integer> nums, boolean[] used) {// 如果当前path中的数字数量等于nums中的数字数量,则已经找到一组答案if (path.size() == nums.size()) {result.add(new ArrayList<>(path));return;}// 枚举nums中所有的数字for (int i = 0; i < nums.size(); i++) {// 如果当前数字已经使用过,则跳过if (used[i]) {continue;}// 标记当前数字已经使用过used[i] = true;// 将当前数字加入到path中path.add(nums.get(i));// 继续递归查找backtracking(nums, used);// 回溯path.remove(path.size() - 1);used[i] = false;}}public List<List<Integer>> permute(List<Integer> nums) {result.clear();path.clear();boolean[] used = new boolean[nums.size()];backtracking(nums, used);return result;}public static void main(String[] args) {Solution solution = new Solution();List<Integer> nums = new ArrayList<>(Arrays.asList(1, 2, 3));List<List<Integer>> result = solution.permute(nums);System.out.println(result);}
}
asList是Java中的一个方法,它可以将数组转换为List。返回的List是由指定数组支持的固定大小的列表。 该方法可以作为基于数组和基于集合的API之间的桥梁
5.2全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
- 输入:nums = [1,1,2]
- 输出: [[1,1,2], [1,2,1], [2,1,1]]
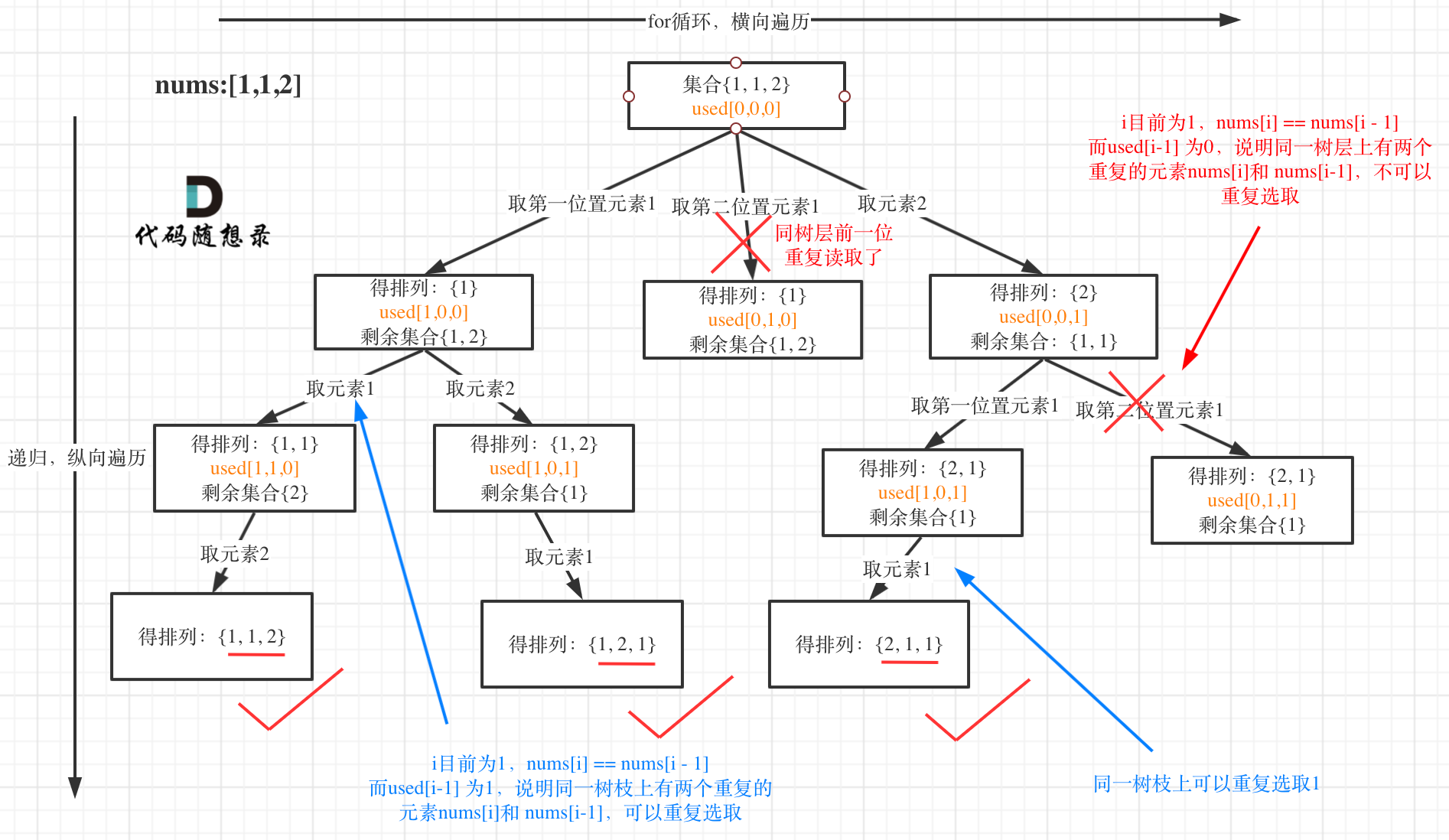
import java.util.*;class Solution {private List<List<Integer>> result = new ArrayList<>();private List<Integer> path = new ArrayList<>();private void backtracking(int[] nums, boolean[] used) {// 如果当前组合中的数字数量等于数组的长度,说明找到了一组,加入结果集中if (path.size() == nums.length) {result.add(new ArrayList<>(path)); // 注意需要新建一个ArrayList,否则结果会受到后续操作的影响return;}for (int i = 0; i < nums.length; i++) {// 如果当前数字已经被使用过,跳过if (used[i]) {continue;}// 如果当前数字和前一个数字相同,并且前一个数字没有被使用过,则跳过if (i > 0 && nums[i] == nums[i-1] && !used[i-1]) {continue;}// 将当前数字加入组合中path.add(nums[i]);used[i] = true; // 标记当前数字已经被使用过// 继续搜索backtracking(nums, used);// 回溯,将当前数字从组合中删除,并标记为未使用过path.remove(path.size() - 1);used[i] = false;}}public List<List<Integer>> permuteUnique(int[] nums) {result.clear(); // 清空结果集path.clear(); // 清空当前组合Arrays.sort(nums); // 对数组进行排序,方便判断重复数字boolean[] used = new boolean[nums.length]; // 标记每个数字是否被使用过backtracking(nums, used); // 开始搜索return result;}public static void main(String[] args) {Solution solution = new Solution();int[] nums = {1, 1, 2};List<List<Integer>> result = solution.permuteUnique(nums);System.out.println(result);}
}六、棋盘问题
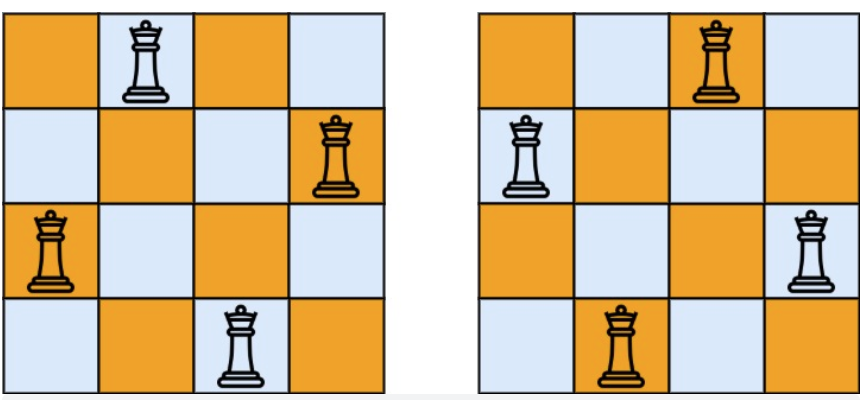
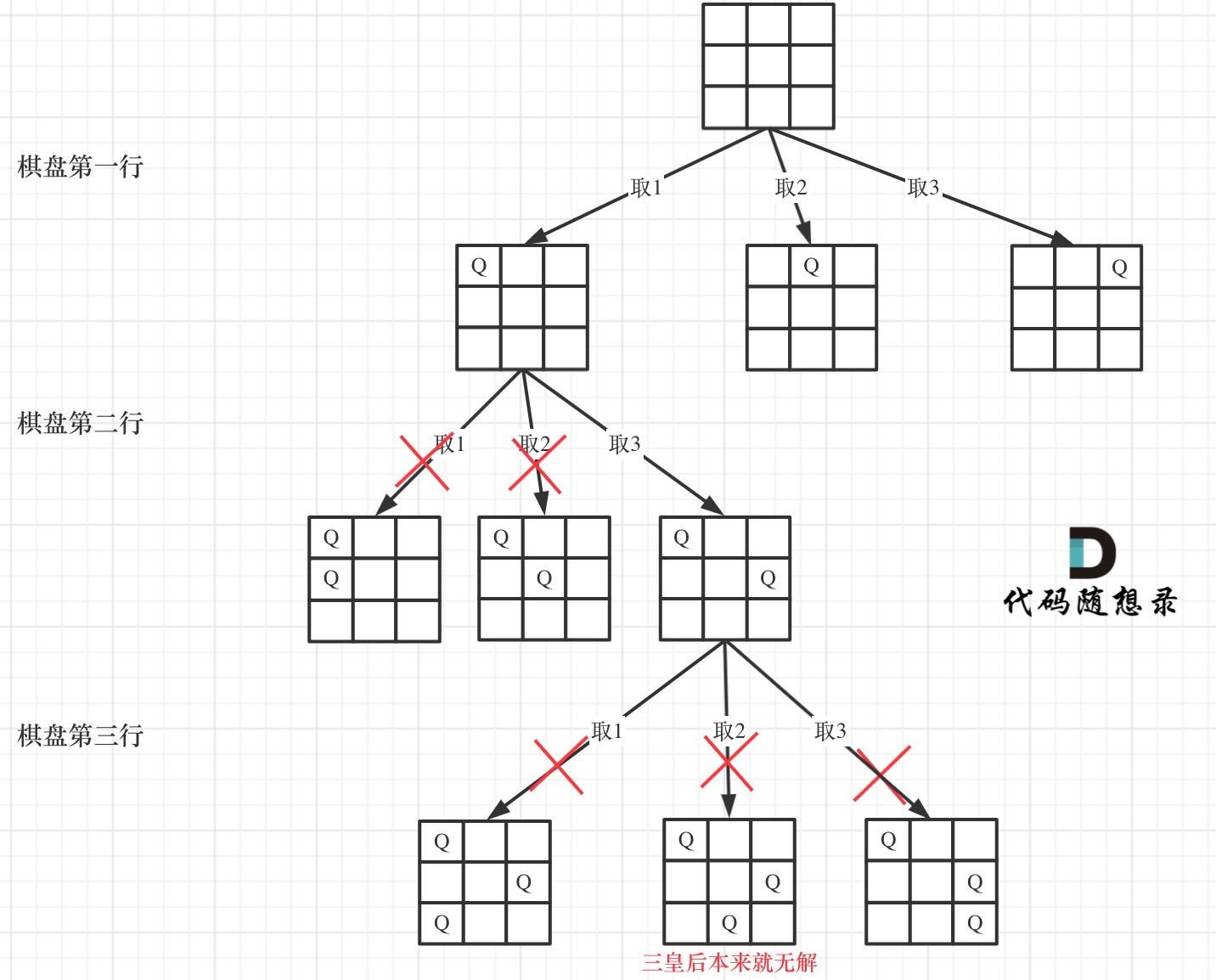
6.1N皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
- 输入:n = 4
- 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
- 解释:如上图所示,4 皇后问题存在两个不同的解法。
提示
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
import java.util.ArrayList;
import java.util.List;class Solution {private List<List<String>> result = new ArrayList<>();// n 为输入的棋盘大小// row 是当前递归到棋盘的第几行了private void backtracking(int n, int row, char[][] chessboard) {if (row == n) {result.add(charToStringList(chessboard));return;}for (int col = 0; col < n; col++) {if (isValid(row, col, chessboard, n)) { // 验证合法就可以放chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard);chessboard[row][col] = '.'; // 回溯,撤销皇后}}}private boolean isValid(int row, int col, char[][] chessboard, int n) {// 检查列for (int i = 0; i < row; i++) { // 这是一个剪枝if (chessboard[i][col] == 'Q') {return false;}}// 检查 45度角是否有皇后for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q') {return false;}}// 检查 135度角是否有皇后for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (chessboard[i][j] == 'Q') {return false;}}return true;}private List<String> charToStringList(char[][] chessboard) {List<String> board = new ArrayList<>();for (char[] row : chessboard) {board.add(new String(row));}return board;}public List<List<String>> solveNQueens(int n) {result.clear();char[][] chessboard = new char[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {chessboard[i][j] = '.';}}backtracking(n, 0, chessboard);return result;}public static void main(String[] args) {Solution solution = new Solution();int n = 4;List<List<String>> result = solution.solveNQueens(n);for (List<String> board : result) {for (String row : board) {System.out.println(row);}System.out.println();}}
}6.2解数独
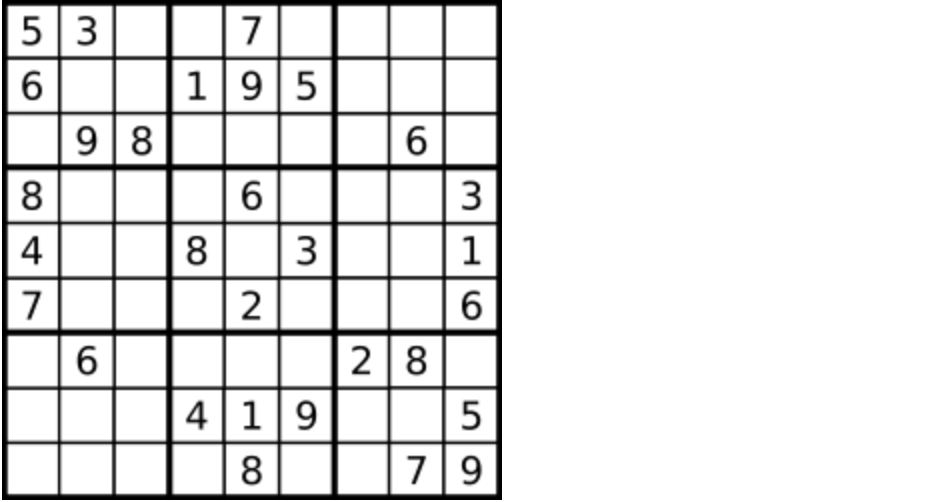
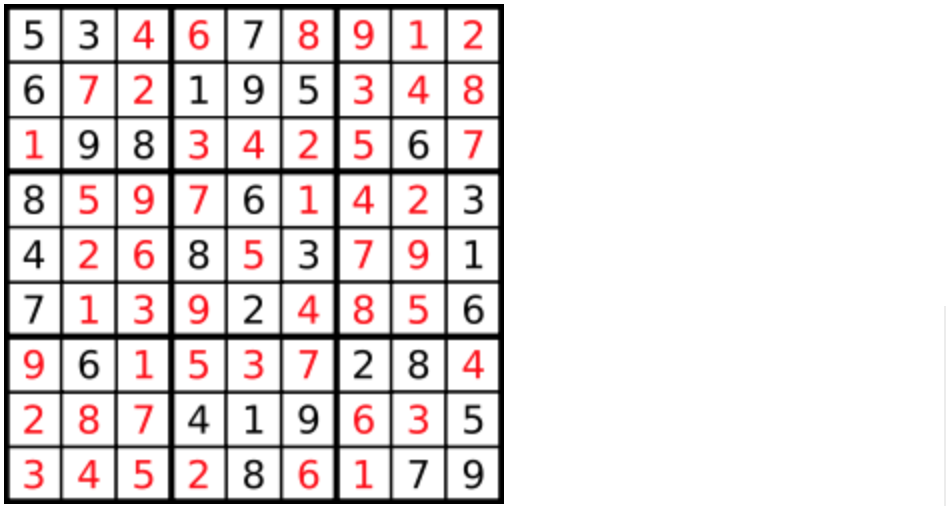
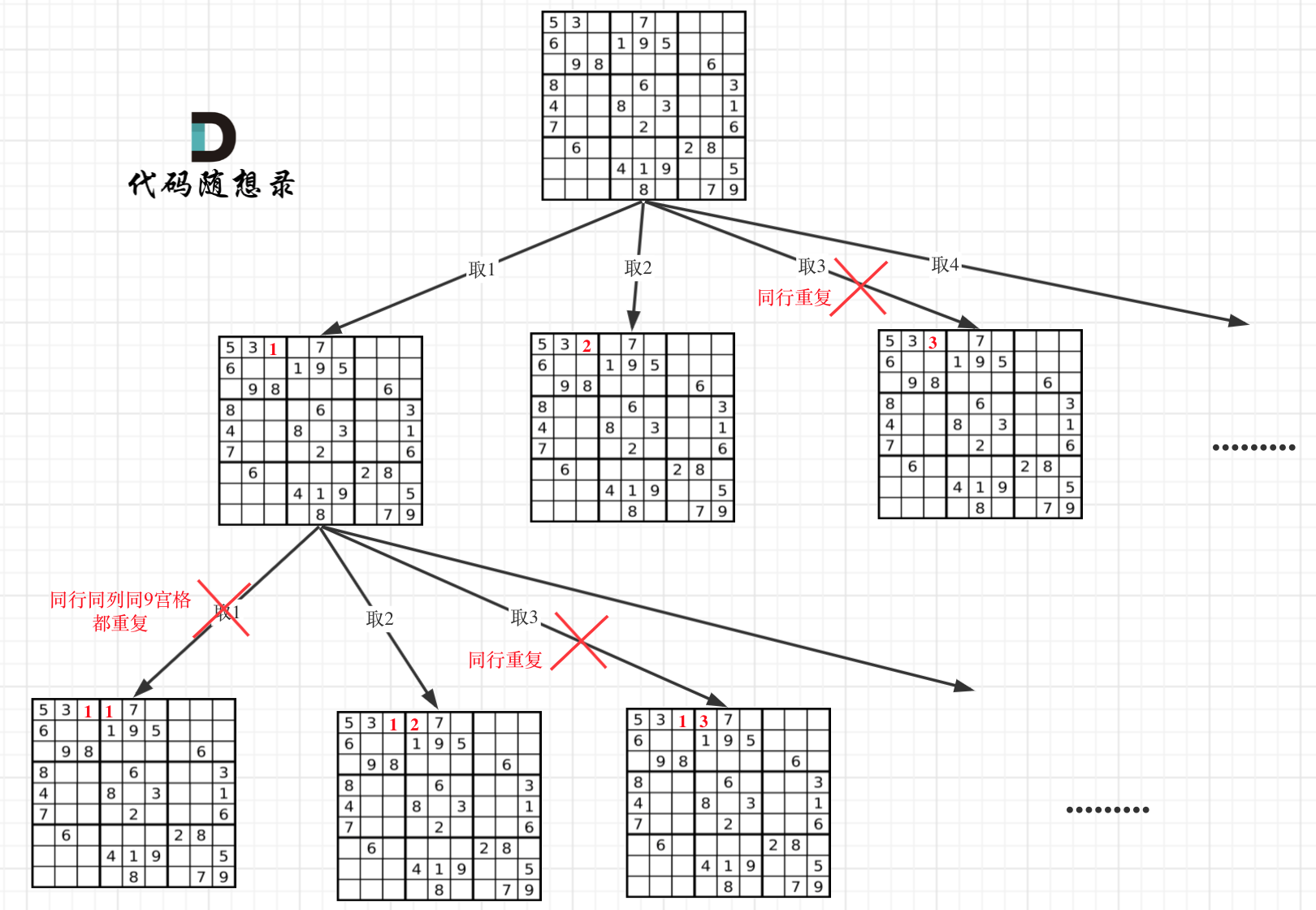
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 '.' 表示。
一个数独。
答案被标成红色。
提示:
- 给定的数独序列只包含数字 1-9 和字符 '.' 。
- 你可以假设给定的数独只有唯一解。
- 给定数独永远是 9x9 形式的。
import java.util.*;class Solution {private boolean backtracking(char[][] board) {for (int i = 0; i < board.length; i++) { // 遍历行for (int j = 0; j < board[0].length; j++) { // 遍历列if (board[i][j] == '.') {for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适if (isValid(i, j, k, board)) {board[i][j] = k; // 放置kif (backtracking(board)) {return true; // 如果找到合适一组立刻返回}board[i][j] = '.'; // 回溯,撤销k}}return false; // 9个数都试完了,都不行,那么就返回false}}}return true; // 遍历完没有返回false,说明找到了合适棋盘位置了}private boolean isValid(int row, int col, char val, char[][] board) {for (int i = 0; i < 9; i++) { // 判断行里是否重复if (board[row][i] == val) {return false;}}for (int j = 0; j < 9; j++) { // 判断列里是否重复if (board[j][col] == val) {return false;}}int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val) {return false;}}}return true;}public void solveSudoku(char[][] board) {backtracking(board);}public static void main(String[] args) {Solution sol = new Solution();char[][] board = new char[][]{{'5','3','.','.','7','.','.','.','.'},{'6','.','.','1','9','5','.','.','.'},{'.','9','8','.','.','.','.','6','.'},{'8','.','.','.','6','.','.','.','3'},{'4','.','.','8','.','3','.','.','1'},{'7','.','.','.','2','.','.','.','6'},{'.','6','.','.','.','.','2','8','.'},{'.','.','.','4','1','9','.','.','5'},{'.','.','.','.','8','.','.','7','9'}};sol.solveSudoku(board);for (int i = 0; i < 9; i++) {System.out.println(Arrays.toString(board[i]));}}
}七、课内实验
7.1 0-1背包(子集问题)
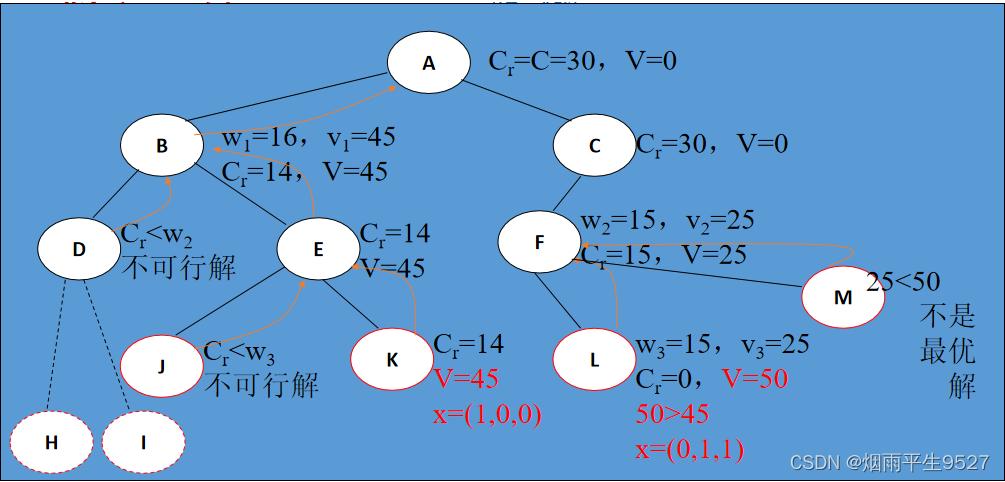
有n个物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?
注:与普通背包问题不同,0-1背包问题中,物品以整体的形式出现,只能选择整体放入背包或整体不放入背包。
c语言代码
#include <stdio.h>
#include <stdlib.h>
#define N 100
int n, c, maxValue = 0; // 物品数量,背包容量,最大价值
int w[N], v[N]; // 物品重量,物品价值
void backtrack(int i, int res, int value) {if (i == n) { // 所有物品都被考虑过了if (value > maxValue) maxValue = value; // 更新最大价值return;}if (res >= w[i]) backtrack(i + 1, res - w[i], value + v[i]); // 考虑第i个物品放入背包backtrack(i + 1, res, value); // 不考虑第i个物品放入背包
}
int main() {scanf("%d%d", &n, &c);for (int i = 0; i < n; i++) scanf("%d%d", &w[i], &v[i]);backtrack(0, c, 0);printf("%d\\n", maxValue);return 0;
}
JAVA
import java.util.Scanner;
public class Main {static int n, c, maxValue = 0; // 物品数量,背包容量,最大价值static int[] w = new int[100], v = new int[100]; // 物品重量,物品价值public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();c = sc.nextInt();for (int i = 0; i < n; i++) {w[i] = sc.nextInt();v[i] = sc.nextInt();}backtrack(0, c, 0);System.out.println(maxValue);}public static void backtrack(int i, int res, int value) {if (i == n) { // 所有物品都被考虑过了if (value > maxValue) maxValue = value; // 更新最大价值return;}if (res >= w[i]) backtrack(i + 1, res - w[i], value + v[i]); // 考虑第i个物品放入背包backtrack(i + 1, res, value); // 不考虑第i个物品放入背包}
}7.2旅行售货员问题
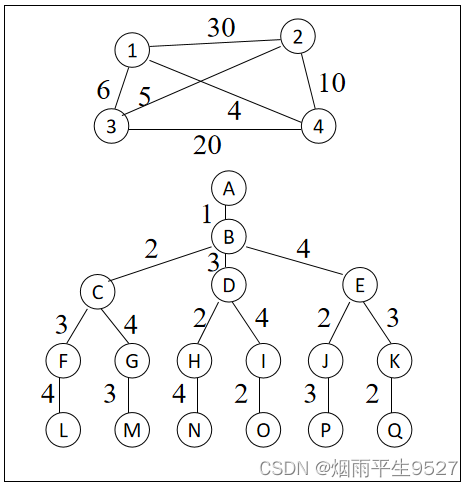
问题描述:某售货员要到若干城市去推销商品,一直各城市之间的路程,他要选定一条从驻地出发,经过每个城市一遍,最后回到住地的路线,使总的路程最短。 该问题是一个NP完全问题, 有(n-1)!条可选路线 最优解(1,3,2,4,1),最优值25
#include <stdio.h>
#include <stdbool.h>
#define MAXN 100 // 最大城市数int n; // 城市数
int graph[MAXN][MAXN]; // 图的邻接矩阵
int path[MAXN],bestPath[MAXN]; // 保存当前路径
bool visited[MAXN]; // 标记城市是否访问过
int minDist = 0x7fffffff; // 保存最短路径的长度void backtracking(int cur, int dist) {if (cur == n) { // 所有城市都已经走过了if (dist + graph[path[n - 1]][0] < minDist) {minDist = dist + graph[path[n - 1]][0]; // 更新最短路径for(int i = 0;i < n;i++){bestPath[i] = path[i];}}return;}for (int i = 1; i < n; i++) { // 枚举下一个城市if (!visited[i]) { // 如果这个城市还没有访问过path[cur] = i; // 选择这个城市visited[i] = true; // 标记这个城市已经访问过backtracking(cur + 1, dist + graph[path[cur - 1]][i]); // 递归到下一层visited[i] = false; // 回溯,撤销选择}}
}int main() {scanf("%d", &n); // 输入城市数for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {scanf("%d", &graph[i][j]); // 输入邻接矩阵}}path[0] = 0; // 起点是城市0visited[0] = true; // 标记起点已经访问过backtracking(1, 0); // 从第2个城市开始递归printf("%d\\n", minDist); // 输出最短路径长度for(int i = 0;i < n;i++){printf("%d ",bestPath[i]+1);}return 0;
}
7.3装载问题(组合问题)
给定n个集装箱要装上一艘载重量为c的轮船,其中集装箱i的重量为wi。集装箱装载问题要求确定在不超过轮船载重量的前提下,将尽可能多的集装箱装上轮船。
由于集装箱问题是从n个集装箱里选择一部分集装箱,假设解向量为X(x1, x2, …, xn),其中xi∈{0, 1}, xi =1表示集装箱i装上轮船, xi =0表示集装箱i不装上轮船。
输入
每组测试数据:第1行有2个整数c和n。C是轮船的载重量(0<c<30000),n是集装箱的个数(n≤20)。第2行有n个整数w1, w2, …, wn,分别表示n个集装箱的重量。
输出
对每个测试例,输出两行:第1行是装载到轮船的最大载重量,第2行是集装箱的编号。
输入样例
3 34
21 10 5
输出样例
1 2
31

#include <stdio.h>
#define MAX_N 20int n; // 货物数量
int c; // 车的载重量
int w[MAX_N],x[MAX_N]; // 每个货物的重量
int best[MAX_N]; // 最优解
int cw; // 当前载重量
int bestw; // 最优载重量
int r; // 剩余物品重量和// 搜索装载方案
void backtrack(int i)
{// 搜索到叶子节点if (i > n) {// 如果找到更优解,则更新最优解if (cw > bestw) {bestw = cw;for (int j = 1; j <= n; j++) {best[j] = x[j];}}return;}// 搜索左子树r -= w[i];if (cw + w[i] <= c) {x[i] = 1;cw += w[i];backtrack(i + 1);cw -= w[i];}r += w[i];// 搜索右子树if (cw + r > bestw) {x[i] = 0;backtrack(i + 1);}
}int main()
{//printf("请输入货物数量和车的载重量(用空格分隔):\\n");scanf("%d%d", &n, &c);//printf("请输入每个货物的重量:\\n");for (int i = 1; i <= n; i++) {scanf("%d", &w[i]);r += w[i];}backtrack(1);printf("最优装载方案为:\\n");for (int i = 1; i <= n; i++) {if (best[i]) {printf("%d ", i);}}printf("\\n最优载重量为:%d\\n", bestw);return 0;
}
7.4图的着色问题(组合问题)
给定图G=(V,E)和m重颜色,若这个图不是m可着色,给出否定回答,若这个图是m可着色的,找出所有不同的着色法。
#include <stdio.h>
#include <stdlib.h>#define MAXN 100int n, m; // 顶点数和着色数
int color[MAXN]; // 存储每个顶点的颜色
int graph[MAXN][MAXN]; // 存储无向图的邻接矩阵
int count = 0; // 记录着色方案数// 判断第i个顶点是否可以涂上color
int isOk(int i, int color[]) {for (int j = 1; j <= n; j++) {if (graph[i][j] == 1 && color[j] == color[i]) {// 如果i和j相邻且颜色相同,返回0return 0;}}return 1;
}// 递归求解m着色问题
void backtrack(int i) {if (i > n) {// 如果所有顶点都涂色了,输出方案count++;printf("方案%d: ", count);for (int j = 1; j <= n; j++) {printf("%d ", color[j]);}printf("\\n");} else {for (int j = 1; j <= m; j++) {color[i] = j; // 尝试给第i个顶点涂上第j种颜色if (isOk(i, color)) {// 如果第i个顶点可以涂上第j种颜色,继续涂色backtrack(i + 1);}color[i] = 0; // 回溯,撤销第i个顶点的颜色}}
}int main() {printf("请输入顶点数和着色数n和m:");scanf("%d%d", &n, &m);// 读入无向图的邻接矩阵printf("请输入无向图的邻接矩阵:\\n");for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {scanf("%d", &graph[i][j]);}}// 求解m着色问题printf("着色所有可能的解:\\n");backtrack(1);// 输出着色可能解的总数printf("着色可能解的总数为%d\\n", count);return 0;
}
请输入顶点数和着色数n和m:4 3
请输入无向图的邻接矩阵:
0 1 1 1
1 0 1 0
1 1 0 1
1 0 1 0
着色所有可能的解:
方案1: 1 2 3 2
方案2: 1 3 2 3
方案3: 2 1 3 1
方案4: 2 3 1 3
方案5: 3 1 2 1
方案6: 3 2 1 2
着色可能解的总数为67.5最大团问题
它是指在一个无向图中找到一个最大的完全子图,其中任意两个顶点之间都有边相连。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>#define MAX_N 100int n, m; // n: 图中节点数, m: 最大团中节点数
bool graph[MAX_N][MAX_N]; // 邻接矩阵表示图
bool visited[MAX_N]; // 标记节点是否在当前团中// 判断节点 v 是否可以加入当前团
bool is_clique(int v, bool selected[MAX_N]) {for (int i = 0; i < n; i++) {if (selected[i] && !graph[v][i]) {return false;}}return true;
}// 计算最大团
void max_clique(bool selected[MAX_N], int size, int index) {if (index == n) { // 所有节点都判断过了if (size > m) { // 更新最大团m = size;for (int i = 0; i < n; i++) {visited[i] = selected[i];}}return;}// 剪枝:如果还有未被选择的节点,且这些节点连向的节点数已经比最大团的大小小,则不可能成为最大团的一部分if (size + (n - index) < m) {return;}// 当前节点不在团中的情况selected[index] = false;max_clique(selected, size, index + 1);// 当前节点在团中的情况if (is_clique(index, selected)) {selected[index] = true;max_clique(selected, size + 1, index + 1);selected[index] = false;}
}int main() {printf("请输入图中节点数 n: ");scanf("%d", &n);printf("请输入邻接矩阵表示的图:\\n");for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {scanf("%d", &graph[i][j]);}}bool selected[MAX_N] = {false}; // 标记节点是否在当前团中max_clique(selected, 0, 0);printf("最大团包含的节点为:");for (int i = 0; i < n; i++) {if (visited[i]) {printf("%d ", i + 1); // 输出节点编号}}printf("\\n最大团大小为:%d\\n", m);return 0;
}
输入:
请输入图的顶点个数: 5
请输入邻接矩阵(0表示不连通,1表示连通):
0 1 1 0 0
1 0 1 1 1
1 1 0 1 0
0 1 1 0 1
0 1 0 1 0输出:
最大团大小为:3
最大团包含的顶点编号为:2 3 4