@代码随想录算法训练营第48天 | 动态规划 LeetCode198.打家劫舍，213.打家劫舍II，337.打家劫舍 III

198.打家劫舍

第一遍读题思考

dp[i]代表打劫到第i家的时候抢到的最多的钱数。
那么递推公式就跟dp[i-1] and dp[i-2]有关，如果抢i-1家的，那么dp[i]=dp[i-1]，如果抢i-2家的dp[i]=dp[i-2]+nums[i]，所以递推公式取最大值。
确定初始化的话可以从递推公式看出要初始化dp[0]和dp[1]两个，dp[0]=nums[0], dp[1] = max(nums[0], nums[1]).

代码随想录解法思路

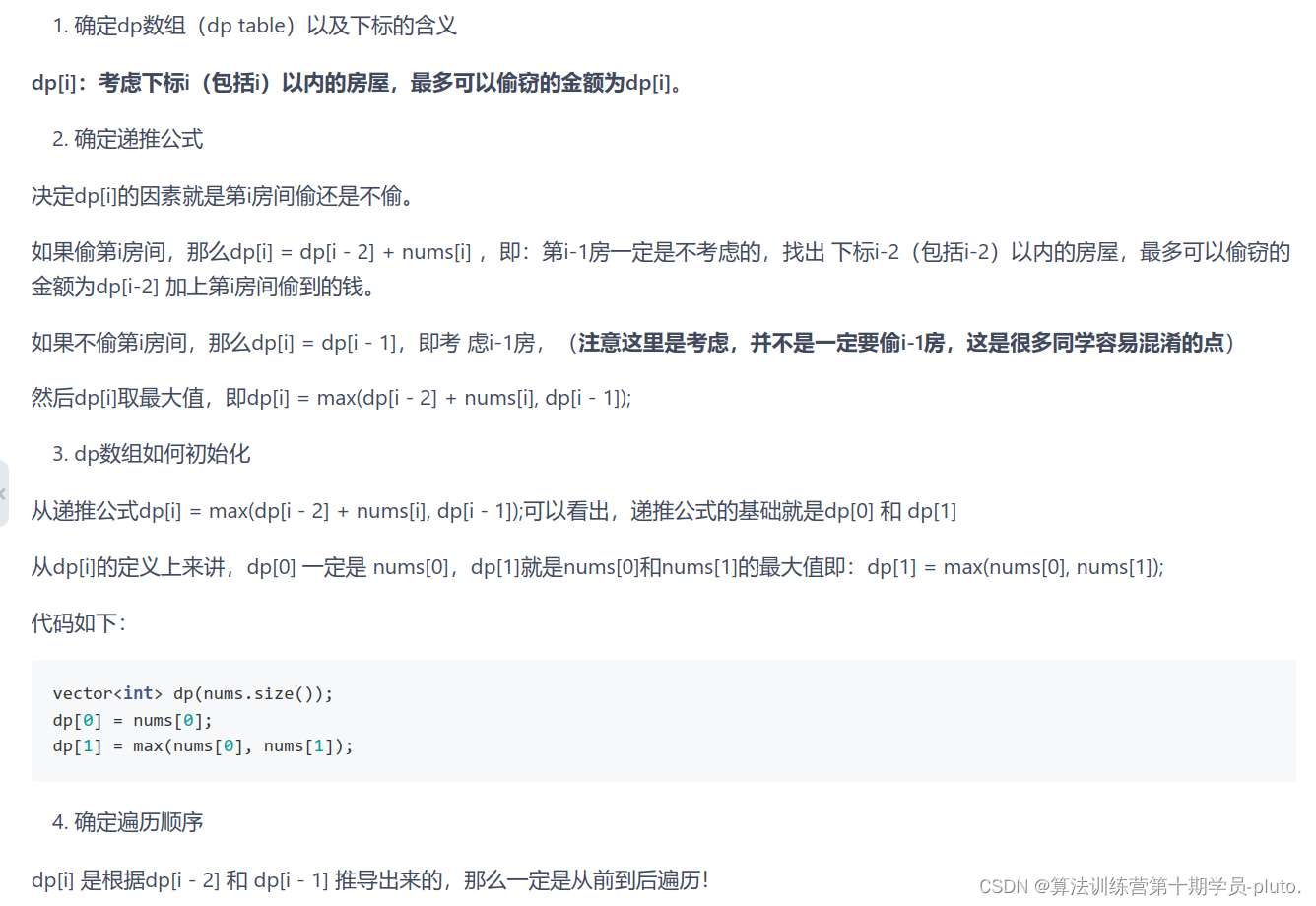
c++代码具体实现注意事项

class Solution {
public:int rob(vector<int>& nums) {vector<int> dp(nums.size(), 0);dp[0] = nums[0];if(nums.size()<2) return dp[nums.size()-1];dp[1] = max(nums[0], nums[1]);for(int i=2;i<nums.size();i++){dp[i] = max(dp[i-1], dp[i-2]+nums[i]);}return dp[nums.size()-1];}
};

213.打家劫舍II

第一遍读题思考

相比于第一版本的题目多了一个成环，也就是抢劫到最后一家的时候要考虑有没有第一家。

代码随想录解法思路

很巧妙的拆解成了两种情况，直接不考虑第一家或者最后一家，不然你遍历到最后一家的时候还要记录前面有没有抢劫第一家的。

c++代码具体实现注意事项

class Solution {
public:int rob(vector<int>& nums) {if(nums.size()==1) return nums[0];if(nums.size()==2) return max(nums[0], nums[1]);vector<int> nums1(nums.begin(),nums.end()-1);vector<int> nums2(nums.begin()+1, nums.end());int rob1 = robori(nums1);int rob2 = robori(nums2);return max(rob1, rob2);}int robori(vector<int>& nums) {vector<int> dp(nums.size(), 0);dp[0] = nums[0];if(nums.size()<2) return dp[nums.size()-1];dp[1] = max(nums[0], nums[1]);for(int i=2;i<nums.size();i++){dp[i] = max(dp[i-1], dp[i-2]+nums[i]);}return dp[nums.size()-1];}
};

337.打家劫舍 III

第一遍读题思考

偷二叉树的家，后续遍历？

代码随想录解法思路

确实遍历是后续遍历的思路，只不过在遍历到中间节点的处理方式很巧妙，分为是否rob当前节点两种情况

c++代码具体实现注意事项

/* Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> robtree(TreeNode* node){if(node==NULL) return vector<int>{0,0};vector<int> left = robtree(node->left);vector<int> right = robtree(node->right);int robcur = node->val + left[0] + right[0];int notrob = max(left[0], left[1]) + max(right[0], right[1]);return vector<int>{notrob, robcur};}int rob(TreeNode* root) {vector<int> dp = robtree(root);return max(dp[0], dp[1]);}
};