2023-04-19 算法面试中常见的递归和回溯问题

递归和回溯
0 递归与回溯的异同
参考文章
- 递归与回溯
- 递归与回溯的理解
- 回溯和递归区别
比较
| 递归 | 回溯 | |
|---|---|---|
| 定义 | 为了描述问题的某一状态,必须用到该状态的上一状态,而描述上一状态,又必须用到上一状态的上一状态……这种用自已来定义自己的方法,称为递归定义。形式如 f(n) = n*f(n-1), if n=0,f(n)=1. | 从问题的某一种可能出发, 搜索从这种情况出发所能达到的所有可能, 当这一条路走到” 尽头 “的时候, 再倒回出发点, 从另一个可能出发, 继续搜索. 这种不断” 回溯 “寻找解的方法, 称作” 回溯法 “。 |
| 不同 | 递归是一种算法结构,递归会出现在子程序中自己调用自己或间接地自己调用自己。最直接的递归应用就是计算连续数的阶乘,计算规律:n!=(n-1)!*n。 | 回溯是一种算法思想,可以用递归实现。通俗点讲回溯就是一种试探,类似于穷举,但回溯有“剪枝”功能,比如求和问题。给定7个数字,1 2 3 4 5 6 7,求和等于7的组合,从小到大搜索,选择1+2+3+4 =10>7,已经超过了7,之后的5 6 7就没必要在继续了,这就是一种搜索过程的优化。如果还有不清楚的可以看一下8皇后问题。 |
| 问题举例 | 玩转算法面试第7章_二叉树与递归 | 玩转算法面试第8章_递归与回溯 |
举例
用一个比较通俗的说法来解释递归和回溯:
我们在路上走着,前面是一个多岔路口,因为我们并不知道应该走哪条路,所以我们需要尝试。尝试的过程就是一个函数。
- 我们选择了一个方向,后来发现又有一个多岔路口,这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上,再做一次尝试,即在函数内部再调用一次函数,这就是递归的过程。
- 这样重复了若干次之后,发现这次选择的这条路走不通,这时候我们知道我们上一个路口选错了,所以我们要回到上一个路口重新选择其他路,这就是回溯的思想。
1~2 树形问题与回溯
17.电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例:输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

class Solution {// 每个按键(数组的下标)对应的可能的字符串,0和1不对应任何字符,所以这里为空String[] letterMap = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz" // 9};public List<String> letterCombinations(String digits) {// 存储最终结果的列表List<String> result = new ArrayList<>();if ("".equals(digits)){return result;}findCombinations(digits, 0, "", result);return result;}/* 寻找digits[index]匹配的字母,获得digits[0...index]对应的解 @param digits 原始数字字符串* @param index 要看digits的哪一个数字* @param s s保存了此时从digits[0...index-1]翻译得到的一个字母字符串* @param result 保存最终可能的字符串*/private void findCombinations(String digits, int index, String s, List<String> result) {// 所有数字都遍历完了,递归退出if (index == digits.length()) {result.add(s);return;}// 拿到index对应的数字字符char c = digits.charAt(index);// 获取当前数字字符可能对应的键盘上的字符串String lettersStr = letterMap[c - '0'];// 第当前数字对应的字符串进行遍历拼接for (int i = 0; i < lettersStr.length(); i++) {findCombinations(digits, index + 1, s + lettersStr.charAt(i), result);}}
}
93.复原IP地址
class Solution {private boolean validId(String ip) {if (ip.length() > 1 && ip.charAt(0) == '0') {return false;}if (ip.length() > 3 || Integer.parseInt(ip) > 255) {return false;}return true;}private String concatList(List<String> numList) {StringBuilder sb = new StringBuilder();for (String numStr : numList) {sb.append(numStr).append(".");}// 最后的一个.要去掉return sb.substring(0, sb.length() - 1);}// 把s分成四分,判断这四份组成的ip的合理性// 递归过程:不断取字符串的前几个字符,每出现一个合法的字符串就接着往下取private void findIp(String s, List<String> numList, List<String> result) {if (numList.size() == 4) {result.add(concatList(numList));// 当s字符串已经被分割成空时,分割完毕,退出本层递归即可return;}for (int i = 1; i <= s.length(); i++) {if (numList.size() == 3) {// 前面已经分成3份了,这里直接把剩下的作为IP即可i = s.length();}String tmp = s.substring(0, i);if (!validId(tmp)) {continue;}numList.add(tmp);// i往后的字符串findIp(s.substring(i), numList, result);// 退出上一层递归,就要从numList中删除最后一个numnumList.remove(numList.size() - 1);}}public List<String> restoreIpAddresses(String s) {List<String> result = new ArrayList<>();if ("".equals(s) || s.length() < 4 || s.length() > 12) {return result;}List<String> numList = new ArrayList<>();findIp(s, numList, result);return result;}
}
131.分割回文串
验证字符串是否用125.验证回文串的代码
class Solution {/* 参考LeetCode125.验证回文串*/public boolean isPalindrome(String s) {s = s.toLowerCase();int l = 0;int r = s.length() - 1;while (l < r) {// 只要还没相遇就接着往下走if (!Character.isLetterOrDigit(s.charAt(l))) {// 左边的字符不是字母或数字l++;continue;}if (!Character.isLetterOrDigit(s.charAt(r))) {// 右边的字符不是字母或数字r--;continue;}// 左右两边都是字母或数字,只要不相等就说明不是回文if (s.charAt(l) != s.charAt(r)) {return false;}// 相等地话,继续向中间靠拢l++;r--;}return true;}/* 获取本次循环中的回文串 @param s 原始字符串* @param palindromes 本次循环中的回文串* @param result 存储所有回文串列表的列表*/void getAllPalindromes(String s, List<String> palindromes, List<List<String>> result) {if ("".equals(s)) {// 当到头时,把回文串列表加入到result中并返回,列表是引用传值,所以必须new一个listresult.add(new ArrayList<>(palindromes));return;}for (int i = 1; i <= s.length(); i++) {String tmp = s.substring(0, i);if (!isPalindrome(tmp)) {// 不是回文串就直接退出本层递归continue;}palindromes.add(tmp);getAllPalindromes(s.substring(i), palindromes, result);// 退出本层递归,需要移除一个回文串palindromes.remove(palindromes.size() - 1);}}public List<List<String>> partition(String s) {List<List<String>> result = new ArrayList<>();List<String> palindromes = new ArrayList<>();getAllPalindromes(s, palindromes, result);return result;}
}
3 组合
用基于递归的回溯法解决组合问题
46.全排列
class Solution {private void calPermutations(List<Integer> numList, List<Integer> curList, List<List<Integer>> result) {if (numList.size() == 0) {result.add(new ArrayList<>(curList));return;}for (int i = 0; i < numList.size(); i++) {curList.add(numList.get(i));List<Integer> numListNext = new ArrayList<>(numList);numListNext.remove(i);calPermutations(numListNext, curList, result);// 递归退出就删除一个元素curList.remove(curList.size() - 1);}}public List<List<Integer>> permute(int[] nums) {List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();List<Integer> numList = new ArrayList<>();for (int num : nums) {numList.add(num);}calPermutations(numList, curList, result);return result;}
}
47.全排列II
只需要在上面46题的递归退出逻辑上加一句
!result.contains(curList)即可
class Solution {private void calPermutations(List<Integer> numList, List<Integer> curList, List<List<Integer>> result) {if (numList.size() == 0 && !result.contains(curList)) {result.add(new ArrayList<>(curList));return;}for (int i = 0; i < numList.size(); i++) {curList.add(numList.get(i));List<Integer> numListNext = new ArrayList<>(numList);numListNext.remove(i);calPermutations(numListNext, curList, result);// 递归退出就删除一个元素curList.remove(curList.size() - 1);}}public List<List<Integer>> permuteUnique(int[] nums) {List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();List<Integer> numList = new ArrayList<>();for (int num : nums) {numList.add(num);}calPermutations(numList, curList, result);return result;}
}
4~5 组合问题
利用递归回溯法解决组合问题.
77.组合
和46、47差不多,简单适配下即可,通过变化索引的方式去遍历子数组要比新建一个子数组效率高很多
class Solution {private void calCombinations(int[] nums, int start, List<Integer> curList, List<List<Integer>> result, int k) {if (curList.size() == k) {result.add(new ArrayList<>(curList));return;}for (int i = start; i < nums.length; i++) {curList.add(nums[i]);calCombinations(nums,i+1, curList, result, k);// 递归退出就删除一个元素curList.remove(curList.size() - 1);}}public List<List<Integer>> combine(int n, int k) {List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();int[] nums = new int[n];for (int i = 0; i < n; i++) {nums[i] = i+1;}calCombinations(nums, 0, curList, result, k);return result;}
}
39.组合总和
class Solution {private void calCombinations(int[] nums, List<Integer> curList, int start, int target, List<List<Integer>> result) {if (target < 0) {return;}if (target == 0) {result.add(new ArrayList<>(curList));return;}// 从start开始是为了能重复使用start位置的元素for (int i = start; i < nums.length; i++) {curList.add(nums[i]);// 下一层递归还是用这些元素,通过索引来遍历子数组而不要额外建立空间calCombinations(nums, curList, i, target - nums[i], result);// 递归退出就删除一个元素curList.remove(curList.size() - 1);}}public List<List<Integer>> combinationSum(int[] candidates, int target) {// 排序后输出结果比较统一Arrays.sort(candidates);List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();calCombinations(candidates, curList, 0, target, result);return result;}
}
40.组合总和 II
和39类似,就是把i换成i+1,然后再添加到result前判重一下即可
class Solution {private void calCombinations(int[] nums, List<Integer> curList, int start, int target, List<List<Integer>> result) {if (target < 0) {return;}if (target == 0) {if(!result.contains(curList)){result.add(new ArrayList<>(curList));}return;}// 从start开始是为了能重复使用start位置的元素for (int i = start; i < nums.length; i++) {curList.add(nums[i]);// 下一层递归还是用这些元素,通过索引来遍历子数组而不要额外建立空间calCombinations(nums, curList, i + 1, target - nums[i], result);// 递归退出就删除一个元素curList.remove(curList.size() - 1);}}public List<List<Integer>> combinationSum2(int[] candidates, int target) {// 排序后输出结果比较统一Arrays.sort(candidates);List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();calCombinations(candidates, curList, 0, target, result);return result;}
}
216.组合总和 III
和40题类似。执行用时 : 1 ms , 在所有 Java 提交中击败了 99.29% 的用户
class Solution {private void calCombinations(int[] nums, List<Integer> curList, int start, int target, List<List<Integer>> result, int k) {if (target < 0) {return;}if (target == 0) {if(curList.size() == k){result.add(new ArrayList<>(curList));}return;}// 从start开始是为了能重复使用start位置的元素for (int i = start; i < nums.length; i++) {curList.add(nums[i]);// 下一层递归还是用这些元素,通过索引来遍历子数组而不要额外建立空间calCombinations(nums, curList, i + 1, target - nums[i], result, k);// 递归退出就删除一个元素curList.remove(curList.size() - 1);}}public List<List<Integer>> combinationSum3(int k, int n) {List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();int[] nums = {1,2,3,4,5,6,7,8,9};calCombinations(nums, curList, 0, n, result, k);return result;}
}
78.子集
class Solution {private void calSubsets(int[] nums, int start, List<Integer> curList, List<List<Integer>> result){if(start == nums.length){return;}for(int i = start; i < nums.length; i++){curList.add(nums[i]);if(!result.contains(curList)){result.add(new ArrayList<>(curList));}calSubsets(nums, i + 1, curList, result);curList.remove(curList.size() - 1);}}public List<List<Integer>> subsets(int[] nums) {List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();result.add(new ArrayList<>());calSubsets(nums, 0, curList, result);return result;}
}
90.子集II
和上一个题相比就加了个
Arrays.sort(nums);
class Solution {private void calSubsets(int[] nums, int start, List<Integer> curList, List<List<Integer>> result){if(start == nums.length){return;}for(int i = start; i < nums.length; i++){curList.add(nums[i]);if(!result.contains(curList)){result.add(new ArrayList<>(curList));}calSubsets(nums, i + 1, curList, result);curList.remove(curList.size() - 1);}}public List<List<Integer>> subsetsWithDup(int[] nums) {Arrays.sort(nums);List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();result.add(new ArrayList<>());calSubsets(nums, 0, curList, result);return result;}
}
401.二进制手表
class Solution {private void getResult(int[] nums, int start, int k, List<Integer> curList, List<List<Integer>> result){if(curList.size() == k){result.add(new ArrayList(curList));return;}for(int i = start; i < nums.length; i++){curList.add(nums[i]);getResult(nums, i + 1, k, curList, result);curList.remove(curList.size() - 1);}}private List<String> trans(List<List<Integer>> result){List<String> list = new ArrayList<>();for(List<Integer> lightList : result){int[] flags = new int[10];for(int i = 0; i < 10; i++){if(lightList.contains(i)){flags[i] = 1;}else {flags[i] = 0;}}int hour = 8 * flags[0] + 4 * flags[1] + 2 * flags[2] + flags[3];int minute = 32 * flags[4] + 16 * flags[5] + 8 * flags[6] + 4 * flags[7] + 2 * flags[8] + flags[9];if(hour > 11 || minute > 59){continue;}if(minute < 10){list.add(hour + ":0" + minute);}else{list.add(hour + ":" + minute);} }Collections.sort(list);return list;}// 组合问题public List<String> readBinaryWatch(int num) {List<List<Integer>> result = new ArrayList<>();List<Integer> curList = new ArrayList<>();// 下标0~3的元素表示上面四个灯,下标4~9的元素表示下面6个灯int[] nums = {0,1,2,3,4,5,6,7,8,9};getResult(nums, 0, num, curList, result);return trans(result);}
}
6 二维平面的搜索
参考Part2BasicGraph/第06章_图论问题建模和floodfill,这里是floodfill的四连通分量问题,可以用DFS解决,在递归回退时记得要把相关状态重置下
79.单词搜索
class Solution {/* 当前点求上右下左四个点时用到的矢量差,dirs 是directions的意思*/private int[][] dirs = {{-1, 0},{0, 1},{1, 0},{0, -1}};/* 传进来的grid有多少行(Row)多少列(Col)*/private int R, C;/* 岛屿网格的情况*/private char[][] grid;private boolean[][] visited;/* 判断第x行第y列的点(x, y)是否在grid所在的范围内*/private boolean inArea(int x, int y) {return x >= 0 && x < R && y >= 0 && y < C;}/* 图的初始化 @param board 二维的图* @param word 要找的单词* @return*/public boolean exist(char[][] board, String word) {this.grid = board;if (grid == null) {return false;}R = grid.length;if (R == 0) {// 如果行数为0说明图为空,直接返回return false;}C = grid[0].length;if (C == 0) {// 如果列数为0说明图为空,直接返回return false;}visited = new boolean[R][C];for (int i = 0; i < R; i++) {for (int j = 0; j < C; j++) {// 点没有被访问而且字符等于word的第一个字符,才以这个点作为起点进行DFS遍历if (grid[i][j] == word.charAt(0)) {// 以(i,j)作为起点进行DFS,看看遍历结果能否组成提供的单词List<Character> cList = new ArrayList<>();cList.add(word.charAt(0));dfs(i, j, 1, word, cList);if (cList.size() == word.length()) {return true;}// 每次递归DFS遍历完,数组要重新初始化visited = new boolean[R][C];}}}return false;}private void dfs(int x, int y, int start, String word, List<Character> cList) {if (cList.size() == word.length()) {return;}visited[x][y] = true;// 遍历节点(x, y)所有的邻接点,判断是陆地的for (int d = 0; d < dirs.length; d++) {int nextX = x + dirs[d][0];int nextY = y + dirs[d][1];// 点(next_x, next_y)必须在grid区域内 + 没被访问过 + 是陆地(点(x, y)是陆地)if (inArea(nextX, nextY) && !visited[nextX][nextY] && grid[nextX][nextY] == word.charAt(start)) {cList.add(grid[nextX][nextY]);dfs(nextX, nextY, start + 1, word, cList);if (cList.size() == word.length()) {break;}// 状态重置:列表和访问数组cList.remove(cList.size() - 1);visited[nextX][nextY] = false;}}}/* char[][] board = {{'A', 'B', 'C', 'E'}, {'S', 'F', 'C', 'S'}, {'A', 'D', 'E', 'E'}};* String word = "ABCCED";* <p>* char[][] board = {{'C', 'A', 'A'}, {'A', 'A', 'A'}, {'B', 'C', 'D'}};* String word = "AAB";* <p>* char[][] board = {{'A','B','C','E'},{'S','F','E','S'},{'A','D','E','E'}};* String word = "ABCEFSADEESE";*/public static void main(String[] args) {char[][] board = {{'C', 'A', 'A'}, {'A', 'A', 'A'}, {'B', 'C', 'D'}};String word = "AAB";System.out.println(new Solution().exist(board, word));}
}
7 floodfill(实际就是DFS)
二维图的搜索实际就是DFS
200.岛屿数量
实际就是DFS求连通分量的个数
public class Solution {/* 当前点求上右下左四个点时用到的矢量差,dirs 是directions的意思*/private int[][] dirs = {{-1, 0},{0, 1},{1, 0},{0, -1}};/* 传进来的grid有多少行(Row)多少列(Col)*/private int R, C;/* 岛屿网格的情况*/private char[][] grid;private boolean[][] visited;/* 连通分量的个数*/private int cCount = 0;/* 判断第x行第y列的点(x, y)是否在grid所在的范围内*/private boolean inArea(int x, int y) {return x >= 0 && x < R && y >= 0 && y < C;}public int numIslands(char[][] grid) {this.grid = grid;if (grid == null) {return 0;}R = grid.length;if (R == 0) {// 如果行数为0说明图为空,直接返回return 0;}C = grid[0].length;if (C == 0) {// 如果列数为0说明图为空,直接返回return 0;}visited = new boolean[R][C];for (int i = 0; i < R; i++) {for (int j = 0; j < C; j++) {// 点没有被访问而且字符等于word的第一个字符,才以这个点作为起点进行DFS遍历if (grid[i][j] == '1' && !visited[i][j]) {dfs(i, j);cCount++;}}}return cCount;}private void dfs(int x, int y) {visited[x][y] = true;// 遍历节点(x, y)所有的邻接点,判断是陆地的for (int d = 0; d < dirs.length; d++) {int nextX = x + dirs[d][0];int nextY = y + dirs[d][1];// 点(next_x, next_y)必须在grid区域内 + 没被访问过 + 是陆地(点(x, y)是陆地)if (inArea(nextX, nextY) && !visited[nextX][nextY] && grid[nextX][nextY] == '1') {dfs(nextX, nextY);}}}
}
139.被围绕的区域
class Solution {public boolean wordBreak(String s, List<String> wordDict) {boolean[] visited = new boolean[s.length() + 1];return dfs(s, 0, wordDict, visited);}private boolean dfs(String s, int start, List<String> wordDict, boolean[] visited) {visited[start] = true;for (int i = start; i < s.length(); i++) {// 防止递归回退的时候再次经过这个字符if (visited[i + 1]) {continue;}String substr = s.substring(start, i + 1);if (wordDict.contains(substr)) {if (i + 1 == s.length() || dfs(s, i + 1, wordDict, visited)) {return true;}}}return false;}/* 输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true* <p>* 输入:"aaaaaaa" 输出:["aaaa","aaa"]*/public static void main(String[] args) {String s = "aaaaaaa";String[] words = {"aaaa", "aaa"};List<String> wordDict = new ArrayList<>(Arrays.asList(words));System.out.println(new Solution().wordBreak(s, wordDict));}
}
417.太平洋大西洋水流问题
遍历每个点,DFS找到既能到达太平洋又能到达大西洋的点加入到结果中即可
class Solution {/* 当前点求上右下左四个点时用到的矢量差,dirs 是directions的意思*/private int[][] dirs = {{-1, 0},{0, 1},{1, 0},{0, -1}};/* 传进来的grid有多少行(Row)多少列(Col)*/private int R, C;/* 岛屿网格的情况*/private int[][] grid;private boolean[][] visited;/* 判断第x行第y列的点(x, y)是否在grid所在的范围内*/private boolean inArea(int x, int y) {return x >= 0 && x < R && y >= 0 && y < C;}public List<List<Integer>> pacificAtlantic(int[][] matrix) {List<List<Integer>> result = new ArrayList<>();this.grid = matrix;if (grid == null) {return result;}R = grid.length;if (R == 0) {// 如果行数为0说明图为空,直接返回return result;}C = grid[0].length;if (C == 0) {// 如果列数为0说明图为空,直接返回return result;}visited = new boolean[R][C];for (int i = 0; i < R; i++) {for (int j = 0; j < C; j++) {// 点没有被访问而且字符等于word的第一个字符,才以这个点作为起点进行DFS遍历boolean pacific = dfs(i, j, true);visited = new boolean[R][C];boolean atlantic = dfs(i, j, false);visited = new boolean[R][C];if (pacific && atlantic) {List<Integer> list = new ArrayList<>();list.add(i);list.add(j);result.add(list);}}}return result;}/* dfs遍历看起点是否能到到 @param x 行* @param y 列* @param pacific true代表检查能否到达太平洋(),false代表检查能否到到大西洋* @return 是否能到达太平洋或大西洋*/private boolean dfs(int x, int y, boolean pacific) {if (pacific) {// 检查能否到达太平洋if (x == 0 || y == 0) {return true;}} else {// 检查大西洋if (x == R - 1 || y == C - 1) {return true;}}visited[x][y] = true;for (int d = 0; d < dirs.length; d++) {int nextX = x + dirs[d][0];int nextY = y + dirs[d][1];// 点(next_x, next_y)必须在grid区域内 + 没被访问过 + 往地处流 + 能到达边界if (inArea(nextX, nextY) && !visited[nextX][nextY] && grid[nextX][nextY] <= grid[x][y] && dfs(nextX, nextY, pacific)) {return true;}}// 到最后都没能到达边界,则说明无法到到,退出即可return false;}public static void main(String[] args) {int[][] matrix = {{1, 2, 2, 3, 5},{3, 2, 3, 4, 4},{2, 4, 5, 3, 1},{6, 7, 1, 4, 5},{5, 1, 1, 2, 4}};System.out.println(new Solution().pacificAtlantic(matrix)); }
}
8 递归回溯法是人工智能的基础
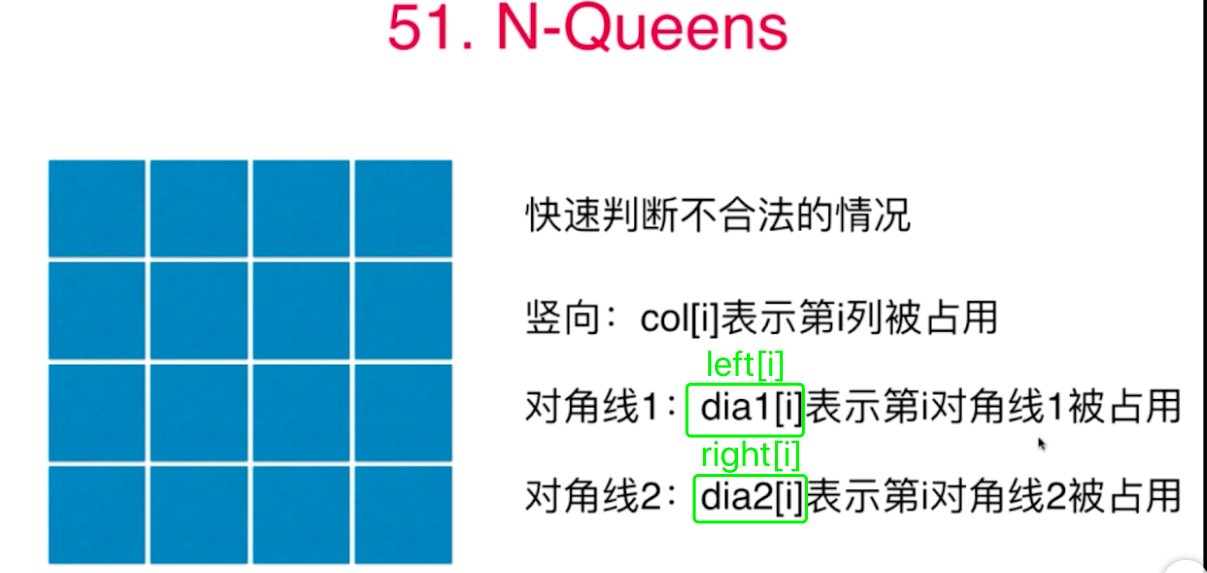
51.N皇后问题
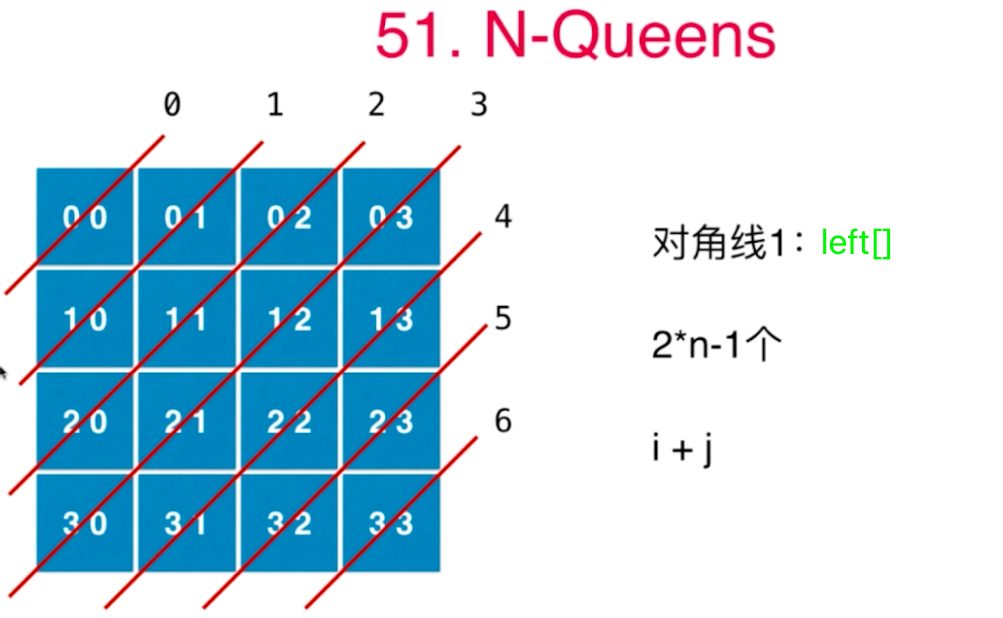
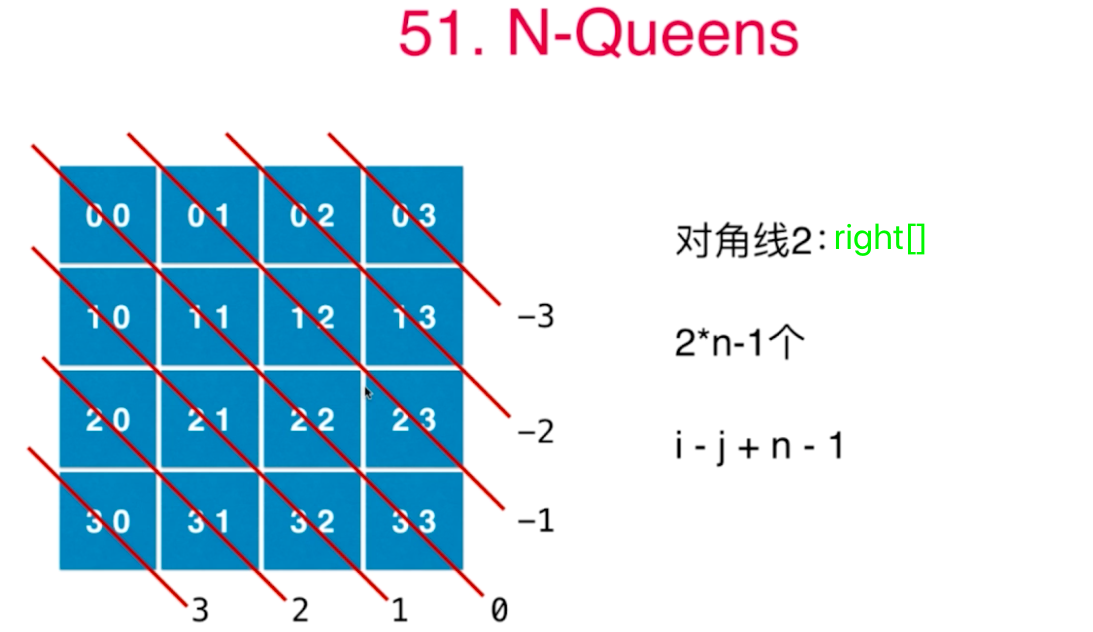
图中的i是下面的r,
class Solution {boolean[] col = null;boolean[] left = null;boolean[] right = null;List<List<String>> ret = new ArrayList<>();public List<List<String>> solveNQueens(int n) {// col[i]表示第i列被占用col = new boolean[n];// 左倾对角线left = new boolean[2 * n - 1];// 右倾对角线right = new boolean[2 * n - 1];// 二维平面char[][] board = new char[n][n];// 回溯法求解问题backTrack(board, 0, n);return ret;}// i代表行,j代表列void backTrack(char[][] board, int i, int n) {if (i >= n) {// 找到能一个能摆放皇后的位置,加入到结果列表中List<String> list = new ArrayList<>();for (int j = 0; j < n; j++) {list.add(new String(board[j]));}ret.add(list);return;}// 初始化棋盘啥都不放Arrays.fill(board[i], '.');for (int j = 0; j < n; j++) {if (!col[j] && !left[i + j] && !right[i - j + n - 1]) {// 一、尝试在当前位置摆放皇后// 摆放皇后board[i][j] = 'Q';// 列占用col[j] = true;// 左倾对角线的规律left[i + j] = true;// 右倾对角线的规律right[i - j + n - 1] = true;// 二、递归求解其合法性backTrack(board, i + 1, n);// 三、递归回退过程中需要恢复初始的状态// 拿走皇后board[i][j] = '.';// 列占用解除col[j] = false;// 左对角线占用解除left[i + j] = false;// 右对角线占用解除right[i - j + n - 1] = false;}}}
}
类似问题还有52和37
52.N皇后II
把51返回的ret改成
ret.size()即可
class Solution {boolean[] col = null;boolean[] left = null;boolean[] right = null;List<List<String>> ret = new ArrayList<>();public int totalNQueens(int n) {// col[i]表示第i列被占用col = new boolean[n];// 左倾对角线left = new boolean[2 * n - 1];// 右倾对角线right = new boolean[2 * n - 1];// 二维平面char[][] board = new char[n][n];// 回溯法求解问题backTrack(board, 0, n);// 和51题唯一不同的地方return ret.size();}// i代表行,j代表列void backTrack(char[][] board, int i, int n) {if (i >= n) {// 找到能一个能摆放皇后的位置,加入到结果列表中List<String> list = new ArrayList<>();for (int j = 0; j < n; j++) {list.add(new String(board[j]));}ret.add(list);return;}// 初始化棋盘啥都不放Arrays.fill(board[i], '.');for (int j = 0; j < n; j++) {if (!col[j] && !left[i + j] && !right[i - j + n - 1]) {// 一、尝试在当前位置摆放皇后// 摆放皇后board[i][j] = 'Q';// 列占用col[j] = true;// 左倾对角线的规律left[i + j] = true;// 右倾对角线的规律right[i - j + n - 1] = true;// 二、递归求解其合法性backTrack(board, i + 1, n);// 三、递归回退过程中需要恢复初始的状态// 拿走皇后board[i][j] = '.';// 列占用解除col[j] = false;// 左对角线占用解除left[i + j] = false;// 右对角线占用解除right[i - j + n - 1] = false;}}}
}
37.解数独
class Solution {final int N = 9;int[] row = new int [N], col = new int [N];//ones数组表示0~2^9 - 1的整数中二进制表示中1的个数:如ones[7] = 3 ones[8] = 1//map数组表示2的整数次幂中二进制1所在位置(从0开始) 如 map[1] = 0,map[2] = 1, map[4] = 2int[] ones = new int[1 << N], map = new int[1 << N];int[][] cell = new int[3][3]; public void solveSudoku(char[][] board) {init();int cnt = fill_state(board);dfs(cnt, board);}void init(){for(int i = 0; i < N; i++) row[i] = col[i] = (1 << N) - 1; for(int i = 0; i < 3; i++)for(int j = 0; j < 3; j++)cell[i][j] = (1 << N) - 1;//以上2个循环把数组的数初始化为二进制表示9个1,即一开始所以格子都可填for(int i = 0; i < N; i++) map[1 << i] = i;//统计0~2^9 - 1的整数中二进制表示中1的个数for(int i = 0; i < 1 << N; i++){int n = 0;for(int j = i; j != 0; j ^= lowBit(j)) n++;ones[i] = n;}}int fill_state(char[][] board){int cnt = 0; //统计board数组空格('.')的个数for(int i = 0; i < N; i++){for(int j = 0; j < N; j++){if(board[i][j] != '.'){int t = board[i][j] - '1';//数独中 i,j位置为数组下标,修改row col cell数组中状态change_state(i, j, t); }else cnt++;}}return cnt;}boolean dfs(int cnt, char[][] board){if(cnt == 0) return true;int min = 10, x = 0, y = 0;//剪枝,即找出当前所以空格可填数字个数最少的位置 记为x yfor(int i = 0; i < N; i++){for(int j = 0; j < N; j++){if(board[i][j] == '.'){int k = ones[get(i, j)];if(k < min){min = k;x = i;y = j;}}}}//遍历当前 x y所有可选数字for(int i = get(x, y); i != 0; i ^= lowBit(i)){int t = map[lowBit(i)];change_state(x, y, t);board[x][y] = (char)('1' + t);if(dfs(cnt - 1, board)) return true;//恢复现场change_state(x, y, t);board[x][y] = '.';}return false;}void change_state(int x, int y, int t){row[x] ^= 1 << t;col[y] ^= 1 << t;cell[x / 3][y / 3] ^= 1 << t;}//对维护数组x行,y列的3个集合(行、列、九宫格)进行&运算//就可以获得可选数字的集合(因为我们用1标识可填数字)int get(int x, int y){return row[x] & col[y] & cell[x / 3][y / 3];}int lowBit(int x){return -x & x;}
}