3.8 并查集

并查集

题目链接

用途

维护集合

1. 将两个集合合并
2. 询问两个元素是否在一个集合当中

实现思路

1. 用树的形式维护集合
2. 每个集合用一棵树表示，树根的编号就是整个集合的编号，每个节点存储他的父节点，p[x]表示节点x的父节点
3. 判断树根的方法:p[x]=x
4. 求某个元素x的集合编号:
   while（p[x]!=x）x=p[x];
   直到最后的x就是树根
5. 合并两个集合： p[x]是x的集合编号(其实就是x)，p[y]是y的集合编号（x，y分别为各集合的根节点），p[x]=y，那就是把x这个集合合并到y那个集合

按照这个思路，很好实现代码：
但是还需要优化地更加快速

#include<iostream>using namespace std;const int N=1e5+10;int p[N];//根节点集合 
int n,m;void merge(int a, int b){//将编号为a和b的两个数所在集合合并 //我们这里将a合并到b中while(p[a]!=a)	a=p[a];//查找根节点//现在的a就是根节点while(p[b]!=b)	b=p[b];//现在的b也是根节点//然后将a合并到b中p[a]=b;}void query(int a,int b){//查询a,b是否在同一个集合中while(p[a]!=a)	a=p[a];while(p[b]!=b)	b=p[b];if(a==b)cout<<"Yes"<<endl;elsecout<<"No"<<endl; }int main(){cin>>n>>m;	for(int i=1;i<=n;i++){p[i]=i;//刚开始每个数都在一个独立的集合中 } while(m--){char c;int a,b;cin>>c>>a>>b;if(c=='M'){merge(a,b);	}else{query(a,b);}}return 0;
} 

优化思路

路径压缩

如果能实现下图的转化，那我们在查找某个节点归属的时候，不就是O(1)的复杂度了吗

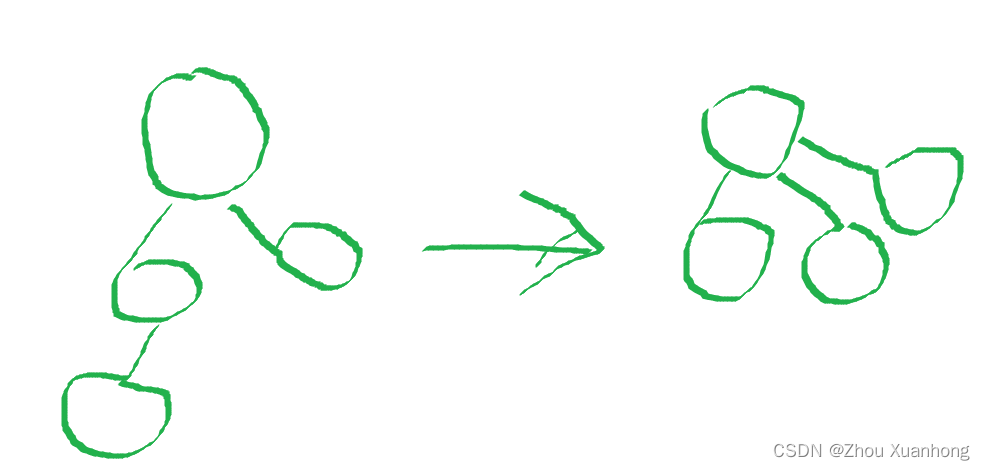
利用find(x)

int find(int x){//找x的根节点并返回if(p[x]!=x)	p[x]=find(p[x]);return p[x]; 
}

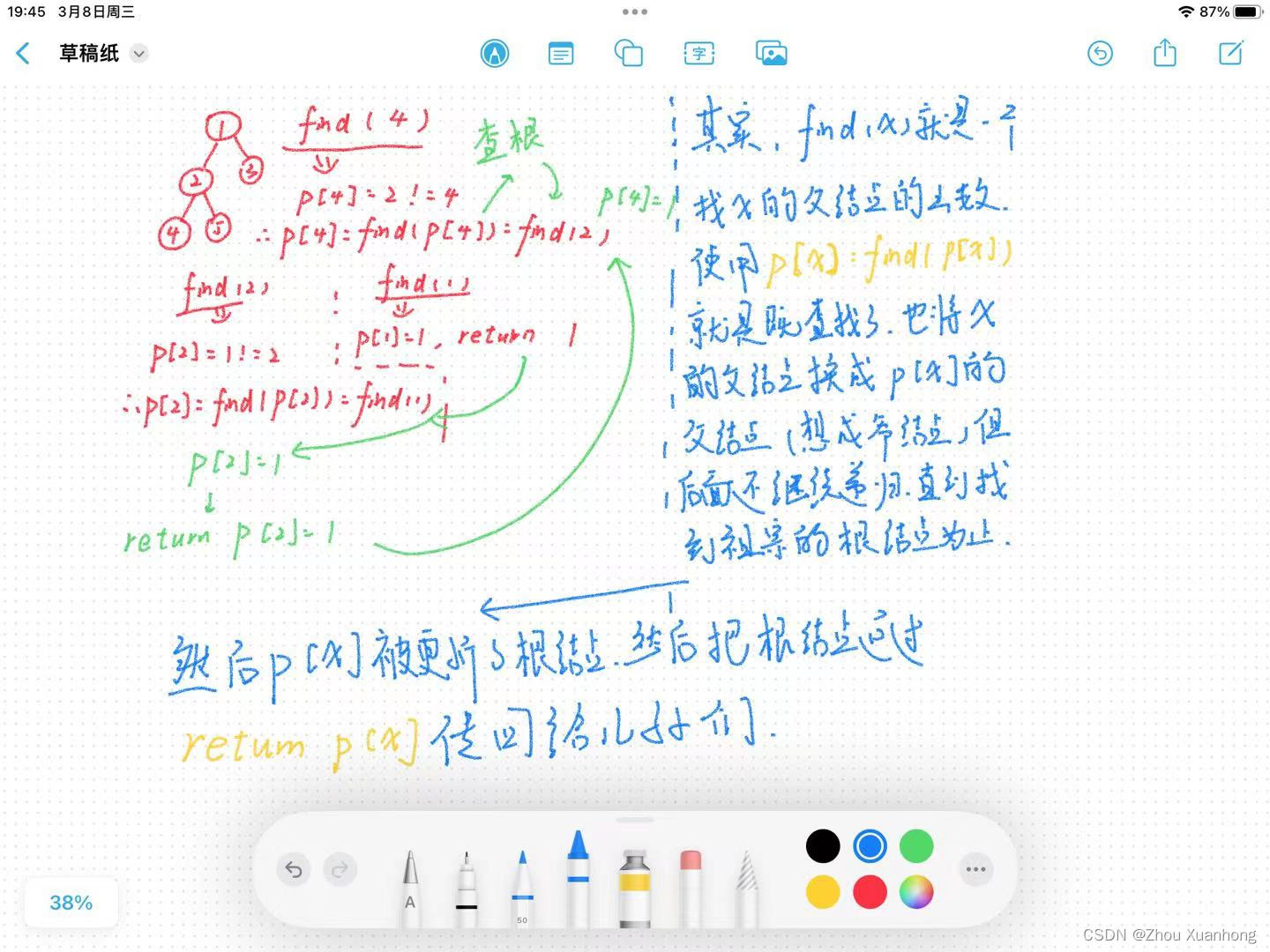
一定要注意写的是IF不是WHILE！！
如果是while，那么如果不是根节点，会永远find，陷入死循环。
递归本身就已经开始寻找了

#include<iostream>using namespace std;const int N=1e5+10;int p[N];//根节点集合 
int n,m;int find(int x){//找x的根节点并返回if(p[x]!=x)	p[x]=find(p[x]);return p[x]; 
}int main(){cin>>n>>m;	for(int i=1;i<=n;i++){p[i]=i;//刚开始每个数都在一个独立的集合中 } while(m--){char c;int a,b;cin>>c>>a>>b;if(c=='M'){//我们让a进入b的集合p[find(a)]=find(b);	}else{if(find(a)==find(b))cout<<"Yes"<<endl;elsecout<<"No"<<endl;}}return 0;
}