算法套路十——回溯法之子集型回溯

算法实例一：LeetCode17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

首先介绍何为回溯法，如下图所示：

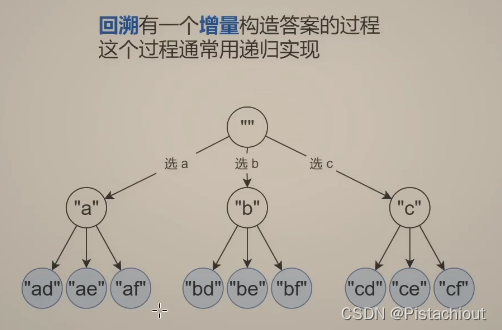
通俗的理解就是通过回溯来遍历所有情况，使用一个数组记录每种情况，且在递归完成后将该数组的内容回溯到，如图中如果目前记录了"ad"的情况，在这种情况枚举完成后，将数组中的“d“删除使数组中元素重新为“a”即是一种回溯，这样可以继续往数组中添加“e”；
当“a”的所有情况枚举完后，将数组中的“a”也删除回溯到数组为空，枚举第一个元素为“b”的情况。这样不断回溯，不断记录，就会枚举完所有的情况。

因此对与本题我们采用回溯法，用path记录当前枚举的情况，ans记录答案。

• 当前问题：前i-1位固定，枚举大于等于 i 位的所有字母组合
• 当前操作：i是否是n，若是则将path记录的情况加入ans中。若不是则枚举第i位所有可能字母，并将枚举的字母加入path，并递归子问题，且在子问题枚举完成后，需要进行回溯——将当前枚举的第i位字母从path删除，并判断第i位是否所有情况都枚举完，若不是则继续枚举当前情况，若是则结束当前问题，返回上层递归函数。
• 子问题：枚举大于等于i+1的字母组合情况

MAPPING = "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"
class Solution:def letterCombinations(self, digits: str) -> List[str]:n=len(digits)if n == 0:return []ans=[]path=[]def dfs(i:int)->None:if i==n:ans.append("".join(path))returnfor c in MAPPING[int(digits[i])]:path.append(c)dfs(i + 1)path.pop()dfs(0)return ans    

算法实例二：LeetCode78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

子集型问题分两种思路，一种是从输入的思路来考虑，如本题考虑当前元素是选还是不选，第二种是从答案的思路来考虑，如考虑选哪个元素

思路一：输入的思路（判断数组每个位置选或不选，直到数组最后一个元素）

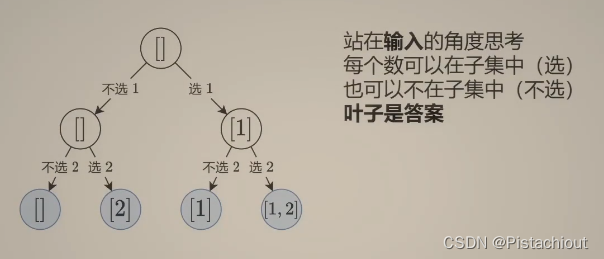
采用回溯法，用path记录当前数字选择的情况，ans记录答案。

• 当前问题：数组前i-1个元素是否选择固定，枚举数组从第i个元素开始的所有元素是否选择
• 当前操作：i是否为n，若是则将当前path加入ans中。若不是则需要枚举子集选择第i位元素或不选第i位元素，若不选第i位元素，则直接递归子问题；若选择第i位元素，则需要先将当前元素加入path中，并递归子问题，在递归完成后，进行回溯，将第i位元素从path中删除
• 子问题：数组前i-1个元素是否选择固定，枚举数组从第i+1个元素开始的所有元素是否选择

class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:ans=[]path=[]n=len(nums)def dfs(i:int)->None:if i==n:ans.append(path.copy())# 固定答案return#不选 nums[i]dfs(i + 1)# 选 nums[i]path.append(nums[i])dfs(i + 1)path.pop() #恢复现场dfs(0)return ans    

思路二：答案的思路（枚举数组所有的选择情况，每次枚举都是答案）

采用回溯法，用path记录当前枚举的情况，ans记录答案。

• 当前问题：枚举数组从第i位到最后的所有选择情况
• 当前操作：每次枚举的path都是答案，故将当前枚举的path加入ans中，并判断是否枚举到最后一个元素，若是则返回；若不是则枚举j>=i，将数组第 j 位元素加入path中，并递归子问题，递归完成后，进行回溯，将数组第j位元素从path删除
• 子问题：枚举数组从第 j+1 位到最后的所有选择情况

class Solution:def subsets(self, nums: List[int]) -> List[List[int]]:ans=[]path=[]n=len(nums)def dfs(i:int)->None:ans.append(path.copy())# 固定答案if i==n:returnfor j in range(i, n):  # 枚举选择的数字path.append(nums[j])dfs(j + 1)/#修改的值在当前dfs(j+1)内加入ans中，如本题即先选1path.pop() #恢复现场，恢复现场后的值将在下一次循环j的dfs(j+1)内加入ans中，即在下一次dfs时没有选择1，选择了2dfs(0)return ans   

总结：

虽然有两种思路，但可以看到仅仅在dfs递归函数中有代码修改，且一般退出递归的条件是一样的，只是在ans更新与何时递归有所不同

算法练习一：LeetCode784. 字母大小写全排列

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

思路一：输入的思路（判断字符串s每个字符是否转变大小写）

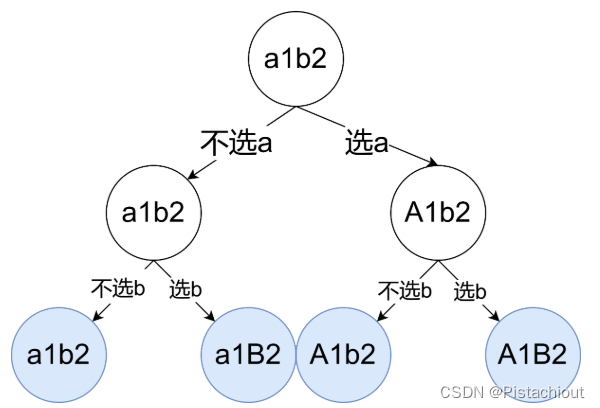
采用回溯法，用cur记录当前转变大小写的情况，ans记录答案。

• 当前问题：判断字符串i之后的每个字符是否转变大小写
• 当前操作：i是否小于n，若是则判断是否为数字，若是则i++，知道当前i不是数字或者直到 i=n，若i=n则将cur加入ans中，否则当前i位置为字符，则分为转变大小写与不转变大小写，并分别递归子问题
• 子问题：判断字符串i+1之后的每个字符是否转变大小写

func letterCasePermutation(s string) []string {n:=len(s)ans:=[]string{}cur:=[]byte(s)var dfs func(i int)dfs=func(i int){for i<n&&cur[i]>='0'&&cur[i]<='9'{i++}if i==n{ans=append(ans,string(cur))return}//不转变dfs(i+1)//转变cur[i] ^= 32//异或 32 可进行字母大小写转换dfs(i+1)cur[i] ^= 32}dfs(0)return ans
}

思路二：答案的思路（枚举选择哪个字母进行转变，每次枚举都是答案）

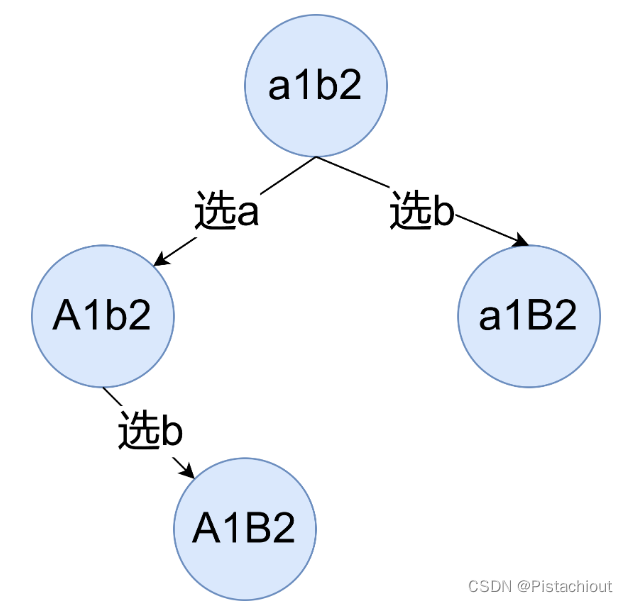
采用回溯法，用cur记录当前枚举的情况，ans记录答案。

• 当前问题：枚举字符串i位后的每个字符的转变情况
• 当前操作：首先将记录的cur字符串计入ans中，之后枚举j从i到字符最后，判断第j位是否是字符，若不是则继续循环，若是则进行转变、递归、回溯
• 子问题：枚举字符串第j+1位之后的分割情况

func letterCasePermutation(s string) []string {n:=len(s)ans:=[]string{}cur:=[]byte(s)var dfs func(i int)dfs=func(i int){ans=append(ans,string(cur))//每次枚举都是答案for j:=i;j<n;j++{if cur[j]>='0'&&cur[j]<='9'{continue    }cur[j] ^= 32dfs(j+1)cur[j] ^= 32}}dfs(0)return ans
}

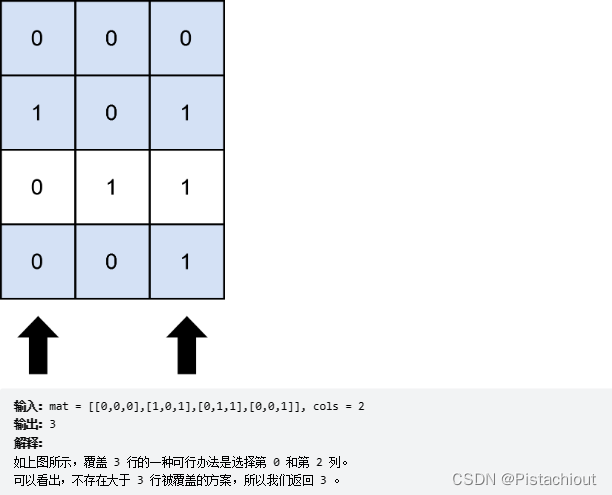
算法练习二：LeetCode2397. 被列覆盖的最多行数

给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ，表示你需要选出的列数。
如果一行中，所有的 1 都被你选中的列所覆盖，那么我们称这一行 被覆盖 了。
请你返回在选择 cols 列的情况下，被覆盖 的行数 最大 为多少。

思路一：输入的思路（判断矩阵每列选或不选，直到矩阵最后一列或者剩余可选列数为0）

采用回溯法，用selectCols来记录当前选择的列数，用lines函数来计算当前列数选择情况下的覆盖行数，maxAns记录答案。

• 当前问题：矩阵前i-1个列是否选择固定，枚举矩阵第i列之后的每个列是否选择
• 当前操作：首先判断剩余可选列数是否为0，若是的话则判断maxAns是否需要更新，若不是则判断i==n，若等于则结束函数；之后分别谈论是否选择该列，若不选择则直接递归子函数，若选择则修改selectCols，并令numSelect–，之后递归子函数，递归完成后进行回溯
• 子问题：矩阵前i个列是否选择固定，枚举矩阵第i+1列之后的每个列是否选择

func maximumRows(matrix [][]int, numSelect int) int {maxAns:=-1n:=len(matrix[0])selectCols:=[13]int{}var dfs func(i int)dfs=func(i int){if numSelect==0{maxAns=max(maxAns,lines(matrix,selectCols))return}else if i==n{return}//不选该列dfs(i+1)//选该列selectCols[i]=1numSelect--dfs(i+1)selectCols[i]=0numSelect++}dfs(0)return maxAns
}
func lines(matrix [][]int,selectCols [13]int) int{ans:=0m:=len(matrix)n:=len(matrix[0])for i:=0;i<m;i++{j:=0for ;j<n;j++{if matrix[i][j]==1{if selectCols[j]==1{continue}break}}if j==n{ans++}}return ans
}
func max(a,b int) int{if a>b{return a};return b}

思路二：答案的思路（枚举选择哪个列，需要满足矩阵最后一列或者剩余可选列数为0的要求）

采用回溯法，用selectCols来记录当前选择的列数，用lines函数来计算当前列数选择情况下的覆盖行数，maxAns记录答案。

• 当前问题：枚举矩阵从第i位之后每列的选择情况
• 当前操作：首先判断剩余可选列数是否为0，若是的话则判断maxAns是否需要更新，若不是则判断i==n，若等于则结束函数；之后枚举j从i到n，并对每个j列进行选择并更新selectCols，递归，回溯
• 子问题：枚举字符串第j+1位之后每列的选择情况

func maximumRows(matrix [][]int, numSelect int) int {maxAns:=-1n:=len(matrix[0])selectCols:=[13]int{}var dfs func(i int)dfs=func(i int){if numSelect==0{maxAns=max(maxAns,lines(matrix,selectCols))return}else if i==n{return}for j:=i;j<n;j++{selectCols[j]=1numSelect--dfs(j+1)selectCols[j]=0numSelect++} }dfs(0)return maxAns
}
func lines(matrix [][]int,selectCols [13]int) int{ans:=0m:=len(matrix)n:=len(matrix[0])for i:=0;i<m;i++{j:=0for ;j<n;j++{if matrix[i][j]==1{if selectCols[j]==1{continue}break}}if j==n{ans++}}return ans
}
func max(a,b int) int{if a>b{return a};return b}

算法练习三：LeetCode1601. 最多可达成的换楼请求数目

我们有 n 栋楼，编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。
给你一个数组 requests ，其中 requests[i] = [fromi, toi] ，表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。
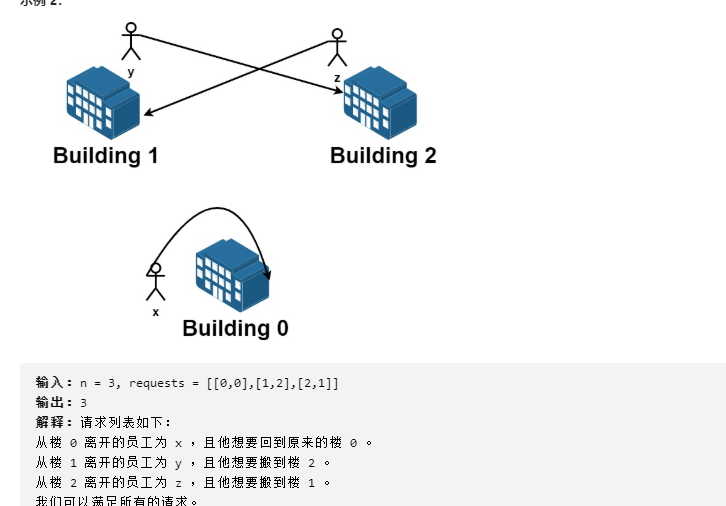
一开始 所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ，一个员工要离开楼 1 ，一个员工要离开楼 2 ，如果该请求列表可行，应该要有两个员工搬入楼 0 ，一个员工搬入楼 1 ，一个员工搬入楼 2 。
请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。1 <= n <= 20,，1 <= requests.length <= 16 ，requests[i].length == 2 ，0 <= fromi, toi < n

思路一：输入的思路（判断每个换房请求选或不选，直到请求最后一列）

采用回溯法，用m记录reques的长度，selects来记录当前选择的换楼请求，用isSatisfy函数来判断当前请求选择情况下是否符合要求，maxAns记录答案。

• 当前问题：矩阵前i-1个请求是否选择固定，枚举矩阵第i列之后的每个请求是否选择
• 当前操作：判断i是否等于m，若是则判断当前选择是否符合条件，若符合则更新maxAns，否则分情况选择当前请求i与不选择当前请求
• 子问题：矩阵前i个请求是否选择固定，枚举矩阵第i+1列之后的每个请求是否选择

func maximumRequests(n int, requests [][]int) int {m:=len(requests)selects:=make([][]int,0)maxAns:=-1var dfs func(int) dfs=func(i int) {if i==m{if isSatisfy(selects){maxAns=max(maxAns,len(selects))    }return}//不选dfs(i+1)//选selects=append(selects,append([]int{},requests[i]...))dfs(i+1)selects=selects[:len(selects)-1]}dfs(0)return maxAns
}
func max(a,b int)int{if(a>b){return a};return b}
func isSatisfy(selects [][]int) bool {cntFrom:=[21]int{}cntTo:=[21]int{}for _,request:=range selects{cntFrom[request[0]]++cntTo[request[1]]++}for i:=0;i<21;i++{if cntFrom[i]!=cntTo[i]{return false}}return true
}

思路二：答案的思路（枚举选换房请求的所有情况，每次枚举都判断是否更新maxAns）

采用回溯法，用m记录reques的长度，selects来记录当前选择的换楼请求，用isSatisfy函数来判断当前请求选择情况下是否符合要求，maxAns记录答案。

• 当前问题：枚举从j到m的换房请求情况
• 当前操作：判断是否符合要求，并判断是否需要更新maxAns；之后判断i==m，若等于则结束递归；否则枚举j从i到m，并记录，递归，回溯
• 子问题：枚举从j+1到m的换房请求情况

func maximumRequests(n int, requests [][]int) int {m:=len(requests)selects:=make([][]int,0)maxAns:=-1var dfs func(int) dfs=func(i int) {if isSatisfy(selects){maxAns=max(maxAns,len(selects))    }if i==m{return}for j:=i;j<m;j++{selects=append(selects,append([]int{},requests[j]...))dfs(j+1)selects=selects[:len(selects)-1]}}dfs(0)return maxAns
}
func max(a,b int)int{if(a>b){return a};return b}
func isSatisfy(selects [][]int) bool {cntFrom:=[21]int{}cntTo:=[21]int{}for _,request:=range selects{cntFrom[request[0]]++cntTo[request[1]]++}for i:=0;i<21;i++{if cntFrom[i]!=cntTo[i]{return false}}return true
}

算法进阶一：LeetCode131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。回文串 是正着读和反着读都一样的字符串。

思路一：输入的思路（判断字符串每个位置是否分割，直到字符串最后一个元素）

采用回溯法，用path记录当前分割情况，ans记录答案。

• 当前问题：判断字符串i之后的每个位置是否进行分割，且使用start记录上一次分割后的开始字符，方便判断是否回文
• 当前操作：i是否为n，若是则将当前path加入ans中。首先判断i是否是最后一位字符，若是则必须进行分割。
  若不是，则分别考虑是否分割，若不分割，则直接调用下一个子问题；若分割，则利用start记录的上一个分割后的开始字符判断当目前字符是否为回文数，若不是则直接跳过，若是则将分割字符加入path中，并调用子问题，且令start为下一位字符i+1，递归完成后恢复现场
• 子问题：判断字符串i+1之后的位置否进行分割，且使用start记录上一个分割的位置，方便判断是否回文

func partition(s string) (ans [][]string) {path:=[]string{}n:=len(s)var  dfs func( int,int )dfs=func(i ,start int ){    if i==n{ans=append(ans,append([]string{},path...))return}// 不选 i 和 i+1 之间的逗号（i=n-1 时已到字符串末尾，必须进行分割）if i < n-1 {dfs(i+1,start)}// 选 i 和 i+1 之间的逗号if isPalindrome(s,start,i){path=append(path,s[start:i+1])dfs(i+1,i+1)path = path[:len(path)-1] // 恢复现场}}dfs(0,0)return 
}
func isPalindrome(s string, left, right int) bool {for left < right {if s[left] != s[right] {return false}left++right--}return true
}

思路二：答案的思路（枚举字符串下一个位置在哪分割，枚举到字符串最后一个元素）

采用回溯法，用path记录当前枚举的情况，ans记录答案。

• 当前问题：枚举字符串第i位之后的分割情况
• 当前操作：注意此题需分割到最后一个位置这样才能确实是否是分割串都是回文串，而不是每个节点都是答案，即i是否为n，若是则将当前path加入ans中。之后循环枚举j从i到n-1为分割结束位置，并判断s[i:j+1]是否为回文串，若是则path记录，递归j+1，回溯
• 子问题：枚举字符串第j+1位之后的分割情况

func partition(s string) (ans [][]string) {path:=[]string{}n:=len(s)var  dfs func( int)dfs=func(i int){    if i==n{ans=append(ans,append([]string{},path...))return}for j:=i;j<n;j++{// 枚举子串的结束位置if isPalindrome(s,i,j){path=append(path,s[i:j+1])dfs(j+1)path=path[:len(path)-1]}}}dfs(0)return 
}
func isPalindrome(s string, left, right int) bool {for left < right {if s[left] != s[right] {return false}left++right--}return true
}