• 二叉树很简单的，试试呗~

文章目录

• Java数据结构 & 二叉树基本知识 & 二叉树遍历
• • 1. 树的基本定义
  • 2. 树的基本概念
  • • 2.1 例子
    • 2.2 树的代码表示：
  • 3. 二叉树
  • • 3.1 特殊节点
    • 3.2 特殊的二叉树
    • 3.3 二叉树的性质
    • • 3.3.1 证明第三点
      • 3.3.2 证明第四点
  • 4. 二叉树遍历
  • • 4.1 定义类二叉树MyBinaryTree
    • 4.2 示例二叉树暴力创建
    • 4.3 三种遍历方式（递归法）
    • • 4.3.1 前序遍历
      • 4.3.2 中序遍历
      • 4.3.3 后序遍历

Java数据结构 & 二叉树基本知识 & 二叉树遍历

1. 树的基本定义

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。

把它叫做树是因为它看 起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点

如下，就是一棵树：

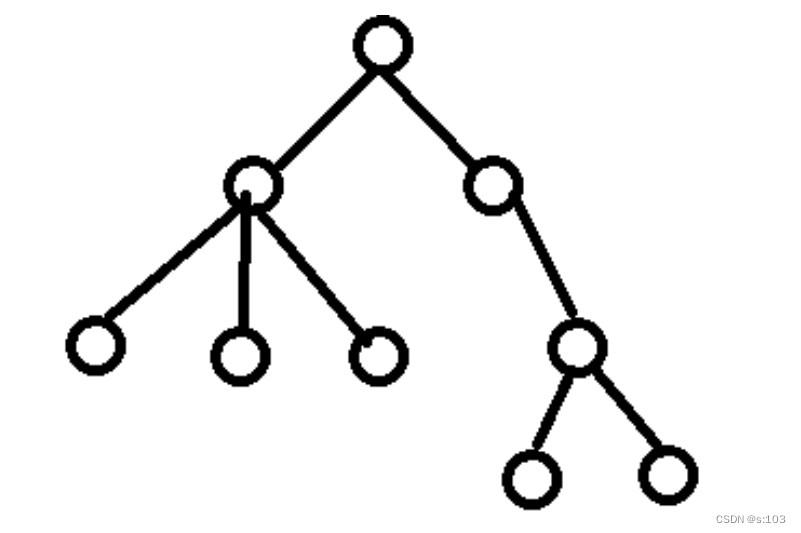
有一个特殊的结点，称为根结点，根结点没有前驱结点 除根结点外，

其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm，其中每一个集合Ti (1 <= i <= m) 又是一棵与树类似的子树。

每棵子树的根结点有且只有一个前驱，可以有0个或多个后继

一颗有N个节点的树有N-1条边

树是递归定义的：

• 根节点分叉后的子树也是树
• 空树也是树，只有根节点也是树

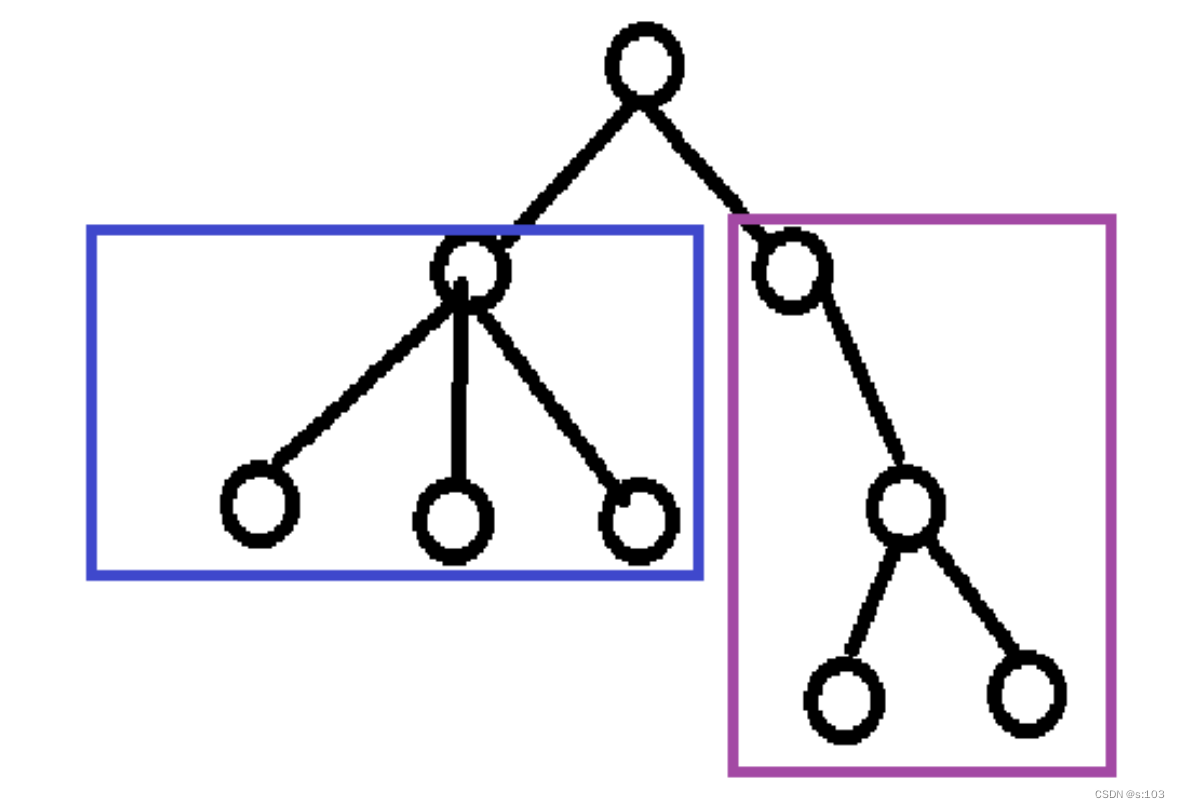
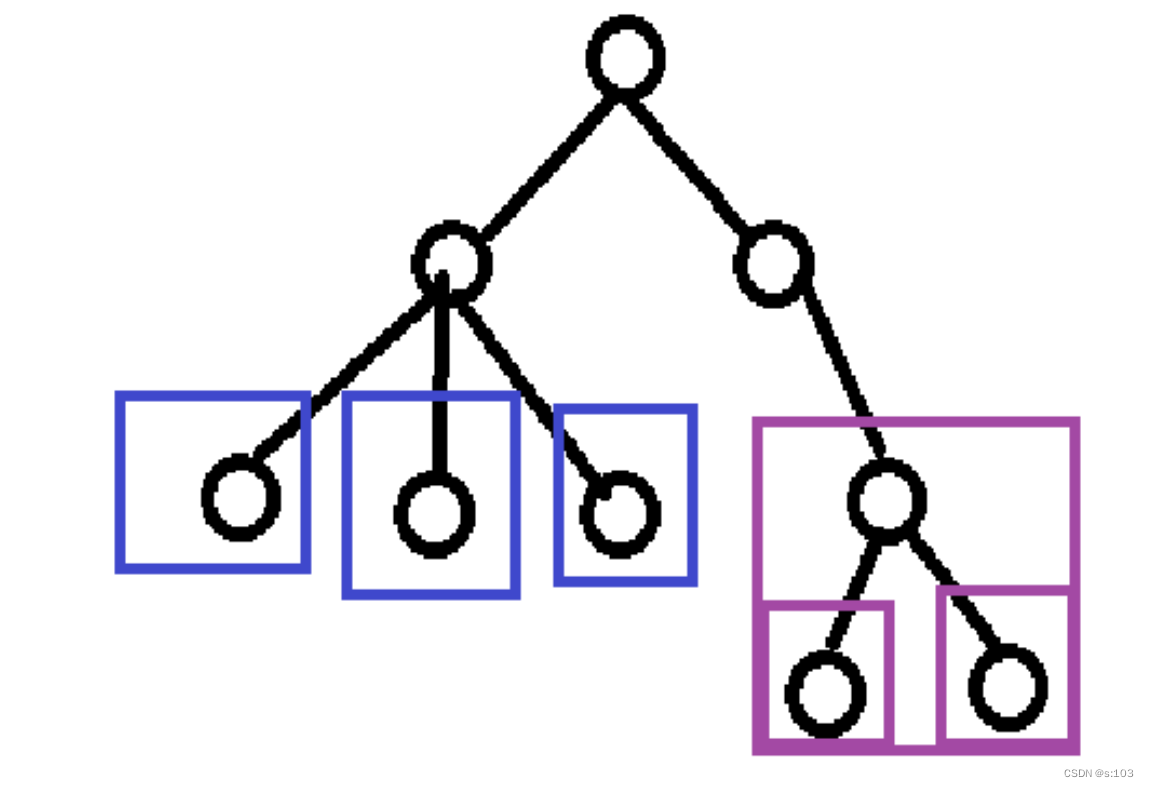
注意： 树形结构中，子树之间不能有交集，否则就不是树形结构

这也代表了一个节点做多有一个前驱~

2. 树的基本概念

1. 结点的度：一个结点含有子树的个数称为该结点的度； 一棵树中，所有结点度的最大值称为树的度；
2. 树的度：度为0的结点称为叶结点；
3. 叶子结点或终端结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；
4. 双亲结点或父结点： 孩子节点一个结点含有的子树的根结点称为该结点的子结点；
5. 孩子结点或子结点：一棵树中，没有双亲结点的结点；
6. 根结点：从根开始定义起，根为第1层，根的子结点为第2层，以此类推
7. 树的高度或深度：树中结点的最大层次；
8. 以下概念只需了解，在看书时只要知道是什么意思即可：
   1. 具有相同父结点的结点互称为兄弟结点；
   2. 双亲在同一层的结点互为堂兄弟；
9. 非终端结点或分支结点：度不为0的结点；
10. 结点的祖先：从根到该结点所经分支上的所有结点；
11. 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。
12. 森林：由m（m>=0）棵互不相交的树组成的集合称为森林

• N叉树就是度为N的树~
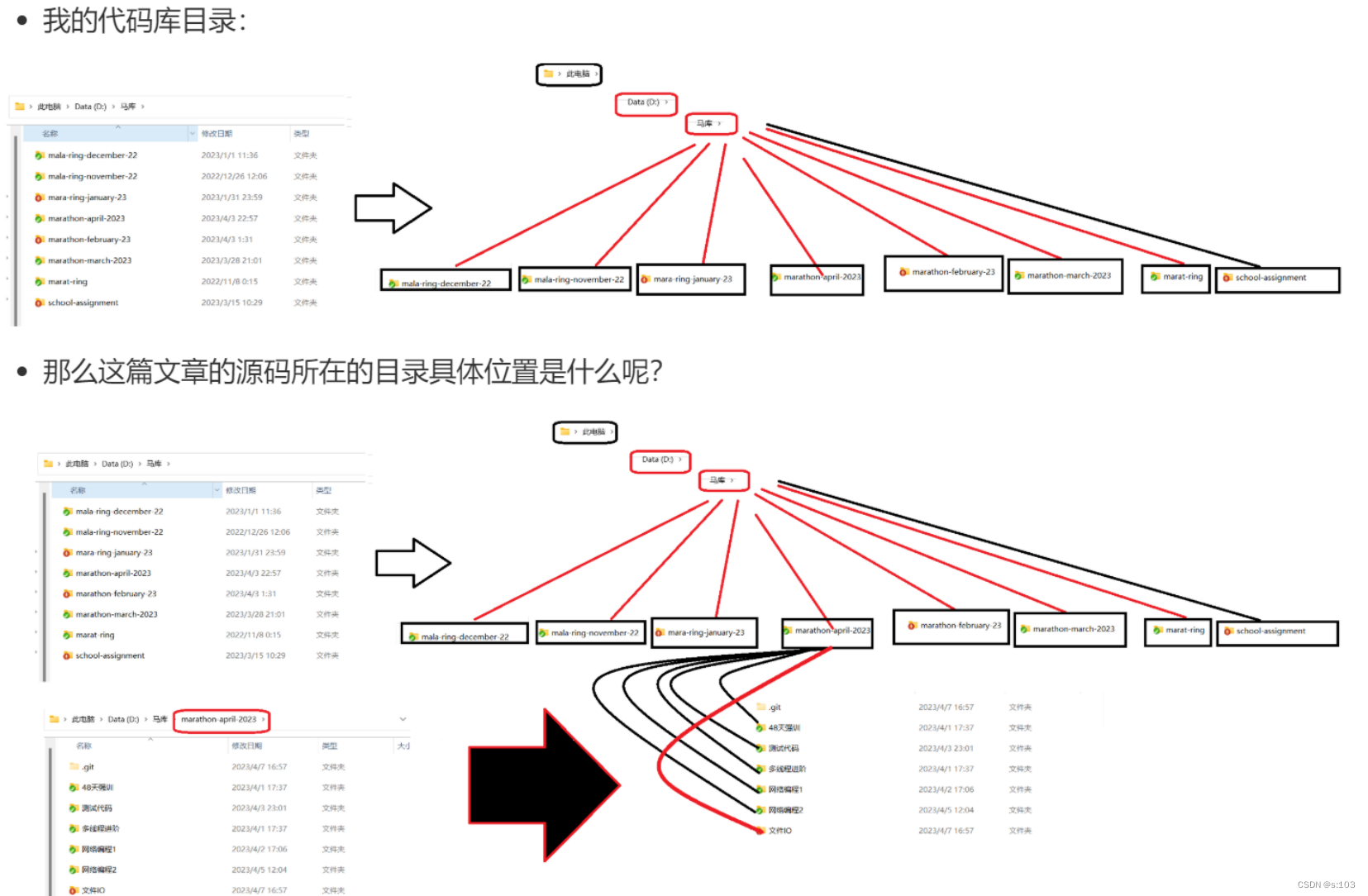
  • 文件系统就是N叉树~

2.1 例子

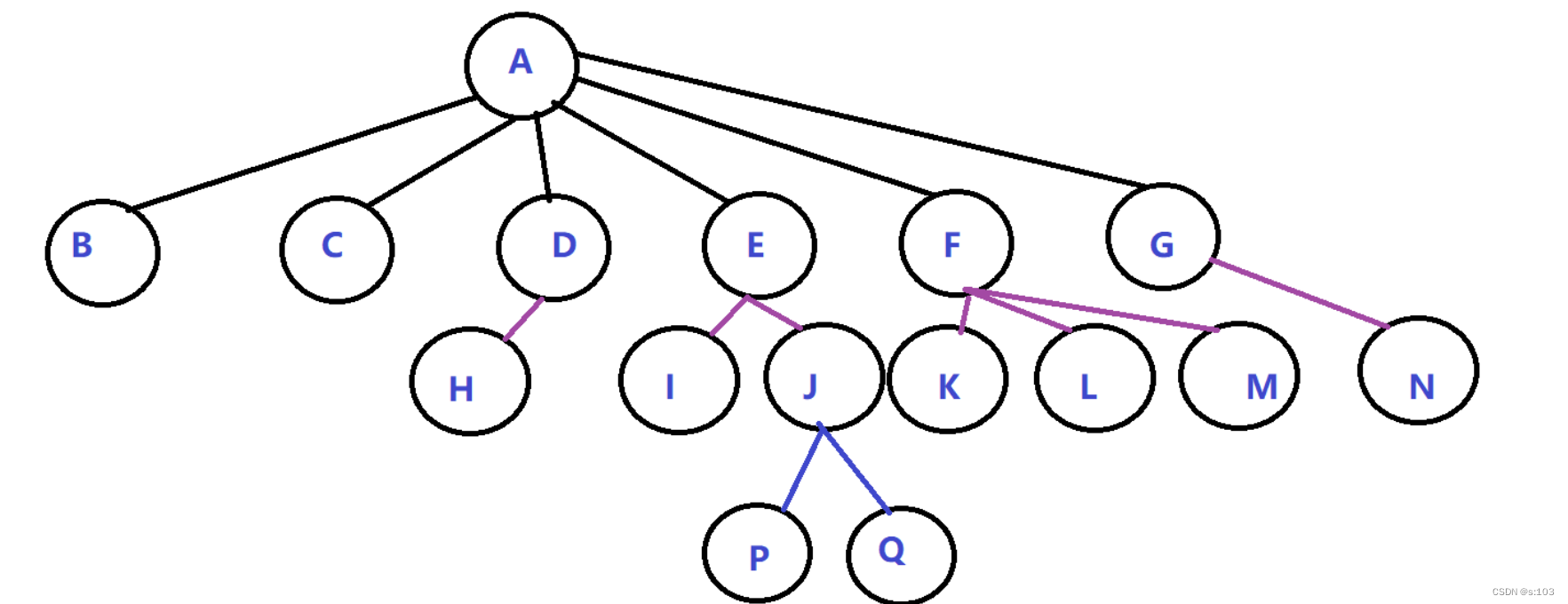
1. A节点的度为6，这也是这棵树最大的度，所以这棵树是六叉树
2. 叶子节点有 B C H I P Q K L M N
3. A 是 B C D E F G 的父节点
4. B C D E F G 是 A 的孩子节点
5. A是根节点
6. 树高/树深为4，即最大层级4
7. B C D E F G 之间互称兄弟节点
8. H I之间就可以互称堂兄弟节点
9. A E J … 就是分支节点
10. A是所有节点的祖先
11. 所有节点都是A的子孙

2.2 树的代码表示：

1. 双亲表示法
2. 孩子表示法
3. 孩子双亲表示法
4. 孩子兄弟表示法
5. 等等…

重点掌握的是 孩子兄弟表示法，后续高阶数据结构会讲解更复杂的树的表达：“引入代表双亲节点的前驱”

• 对于数组表示二叉树的堆结构，是顺序存储的，通过下标可以得到孩子和双亲~
  • 甚至你可以存下来

class Node {int value;//树节点存储的值Node ChildNode1;//第一个孩子Node ChildNode2;//第二个孩子Node ChildNode3;//第三个孩子......Node ChildNodeN;//第N个孩子
}//N取树的度

3. 二叉树

• 二叉树最大分支为2
• 以下所讲的都是链式存储的二叉树

孩子兄弟表示法去表示的二叉树，这是最普遍的树了

• 后续会更新高阶数据结构的高阶树：AVL树，红黑树，B/B+树…

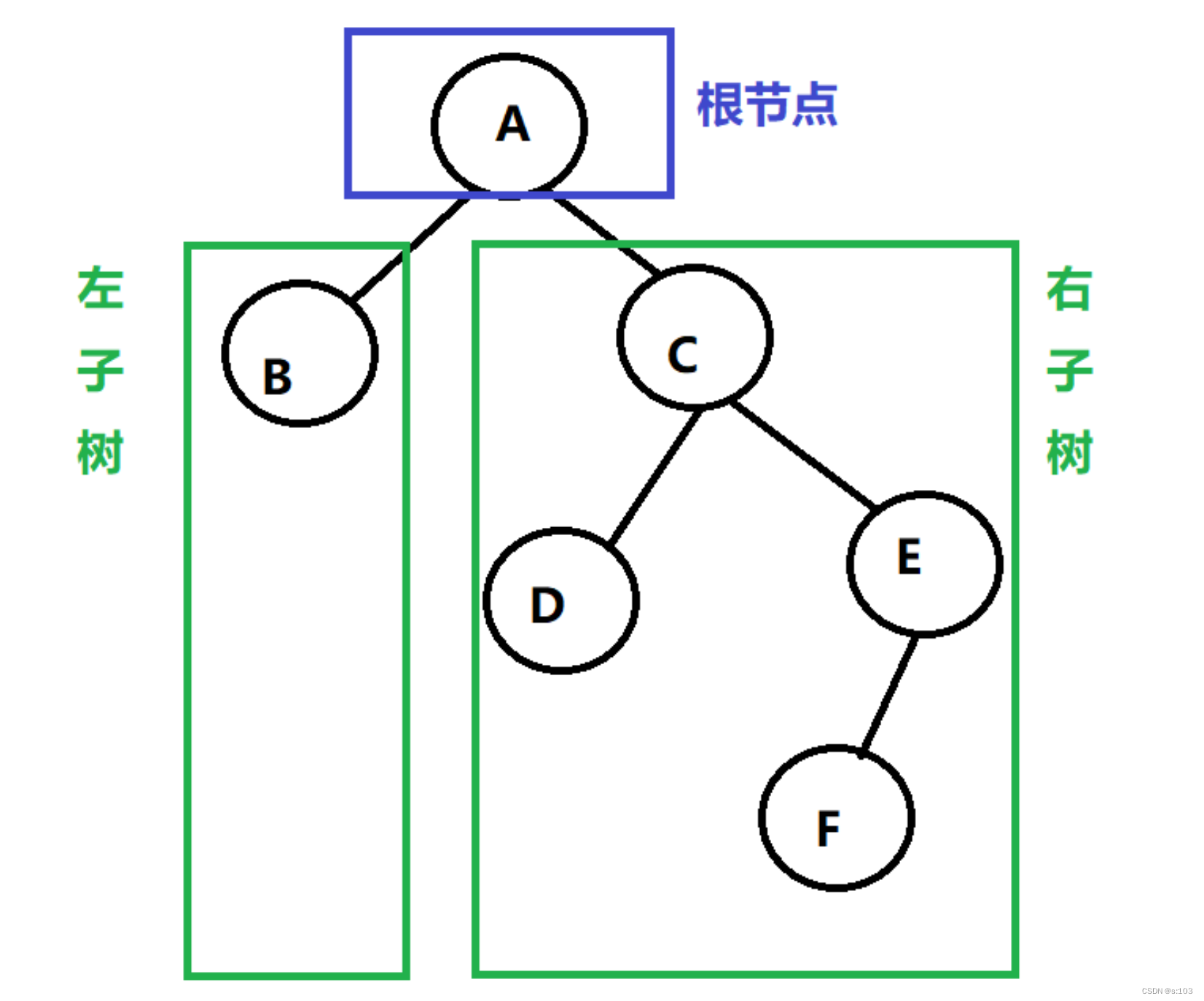
3.1 特殊节点

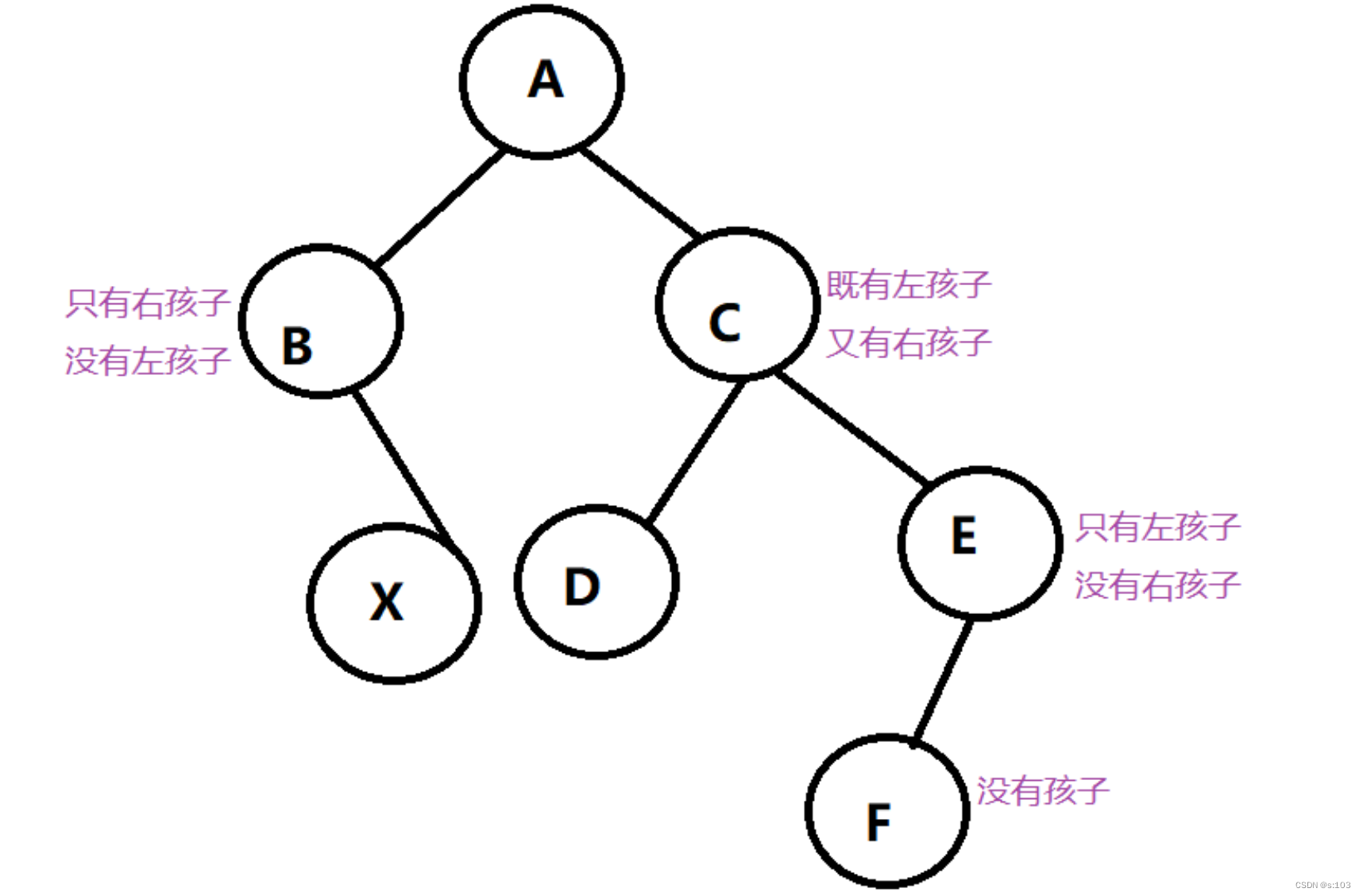
3.2 特殊的二叉树

1. 满二叉树： 每层的节点数都达到最大，这样的二叉树就是满二叉树

• 显然，二叉树的第N层的节点数最大为 2^N-1
  

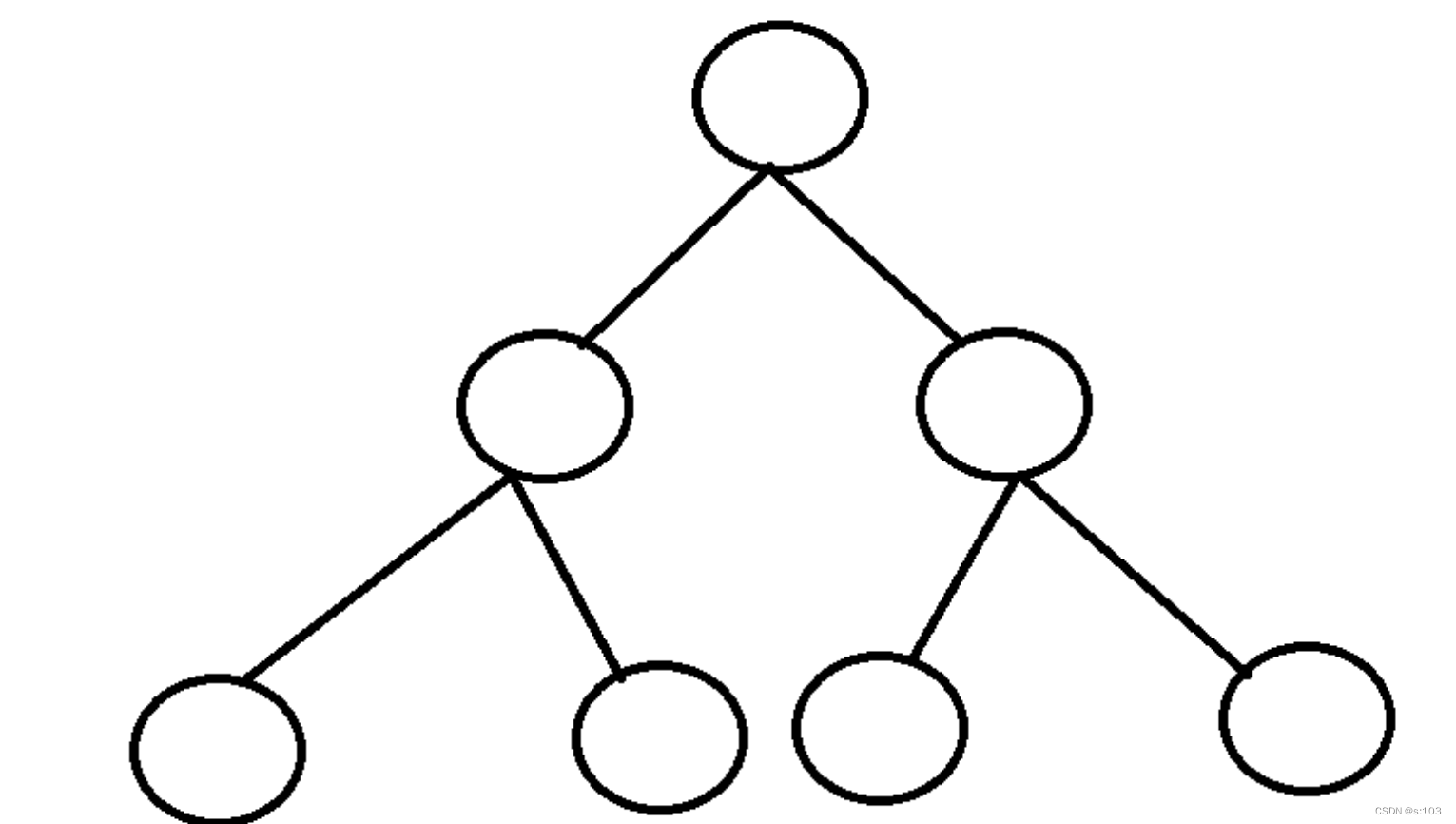
2. 完全二叉树：给每个节点编个号，从上到下，从左到右依次排序（根节点序号为0）

   • 且，每个节点都满足：
   1. 是父亲节点编号的（2 * i + 1 或者 2 * i + 2），【i代表父亲节点的编号】
   2. 是孩子节点编号的（(i - 1) / 2），【i代表孩子节点的编号】
   • 没有父亲节点或者孩子节点的忽略判断

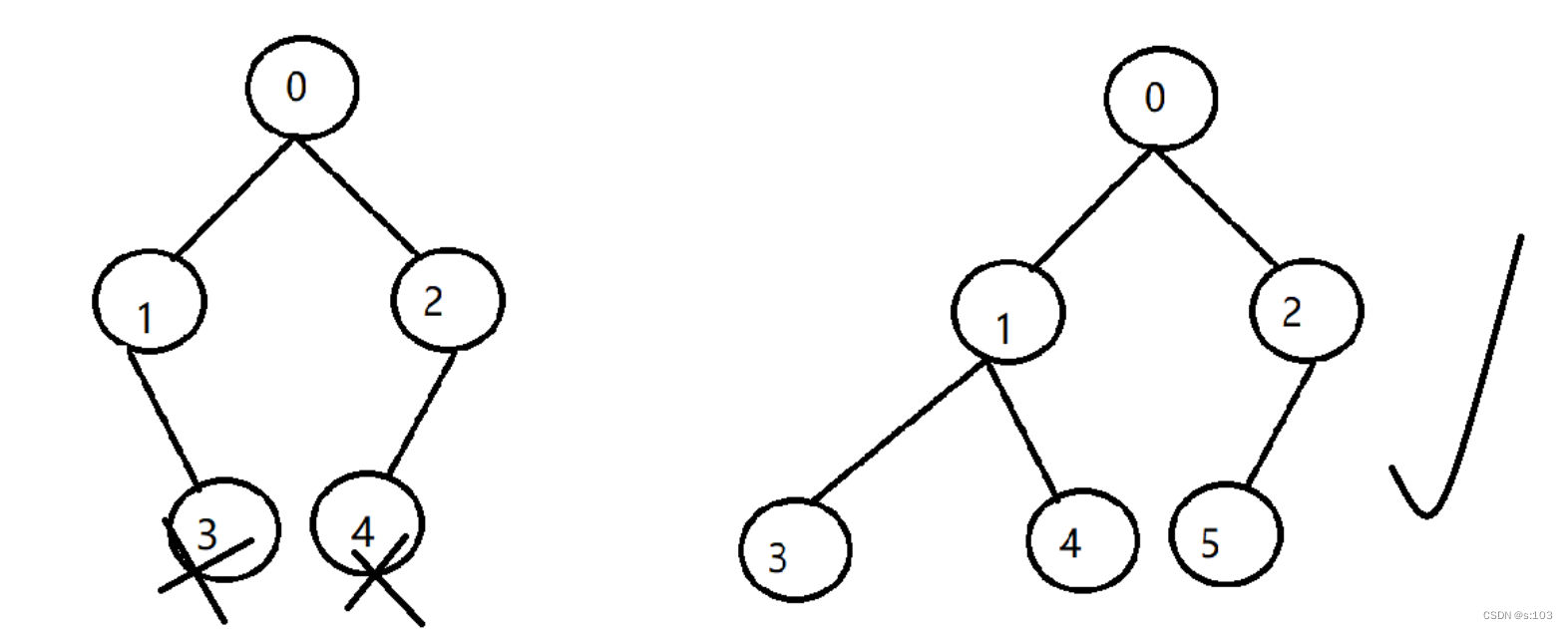
• 根据满二叉树，每一行第几个节点，都应该有确立的编号，完全二叉树应该一一对应上~

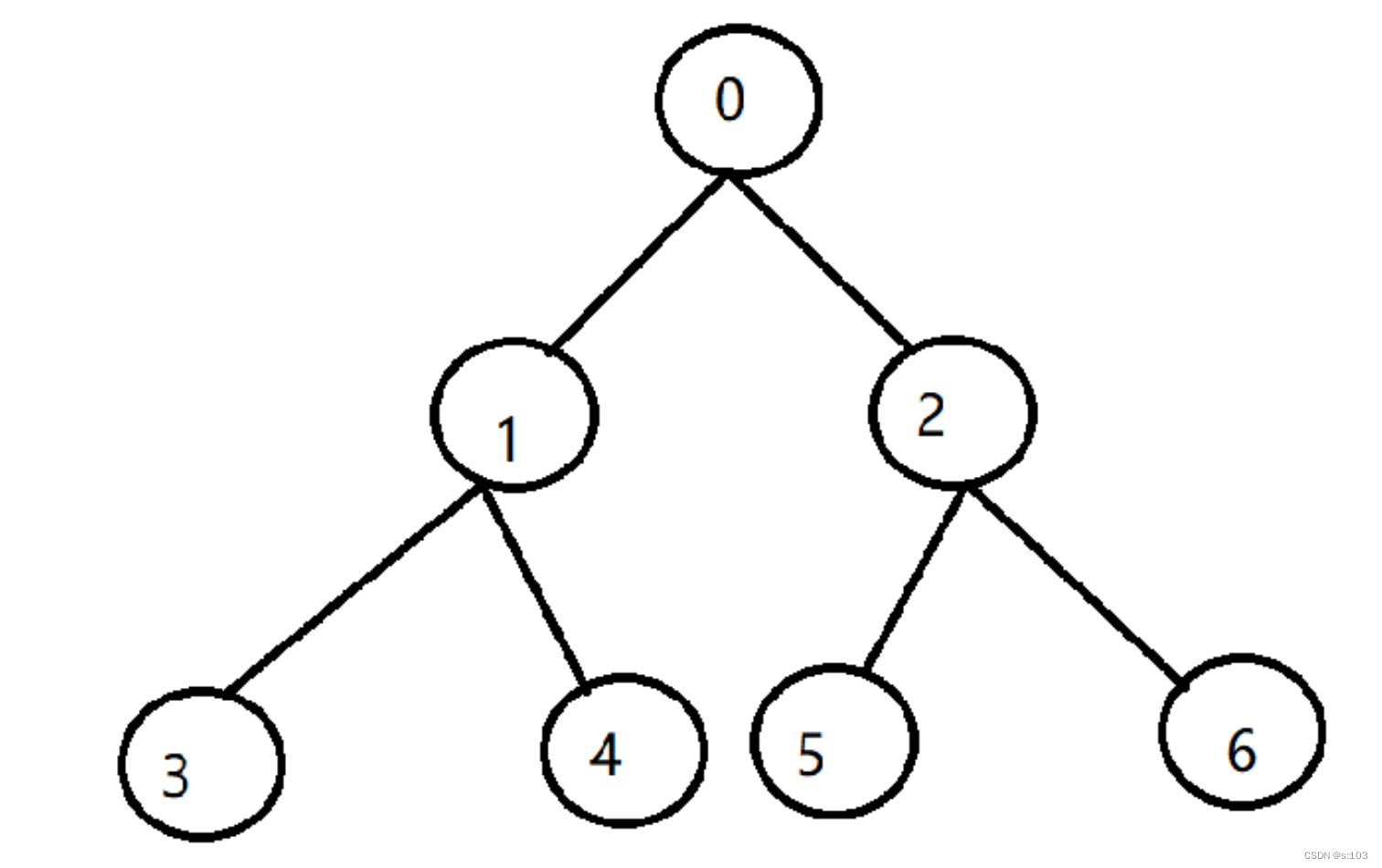
满二叉树就是特殊的完全二叉树

• 满二叉树从最后按顺序去掉，就是完全二叉树。

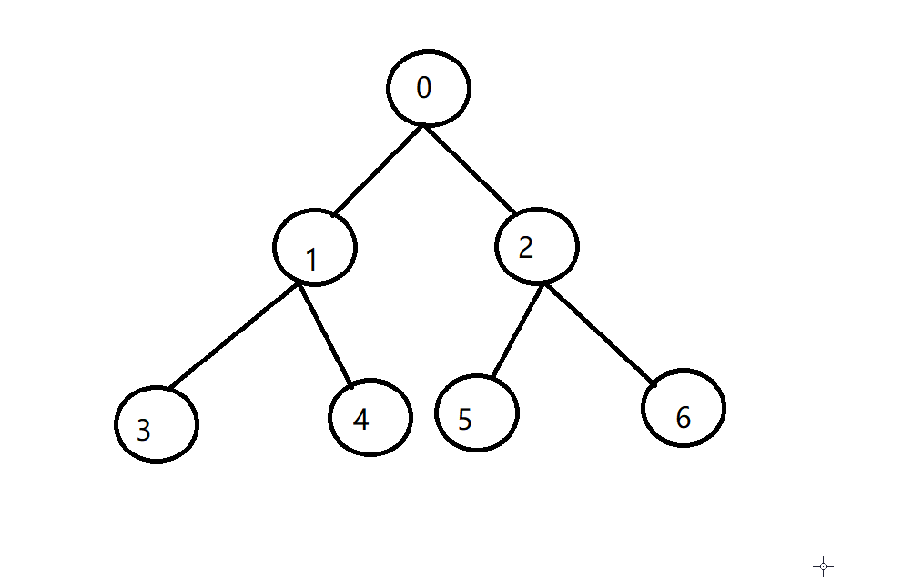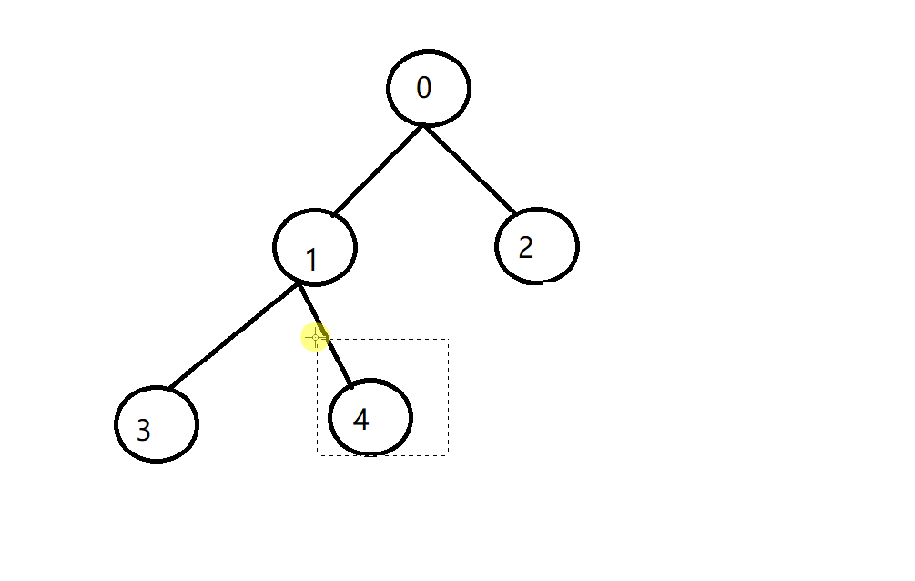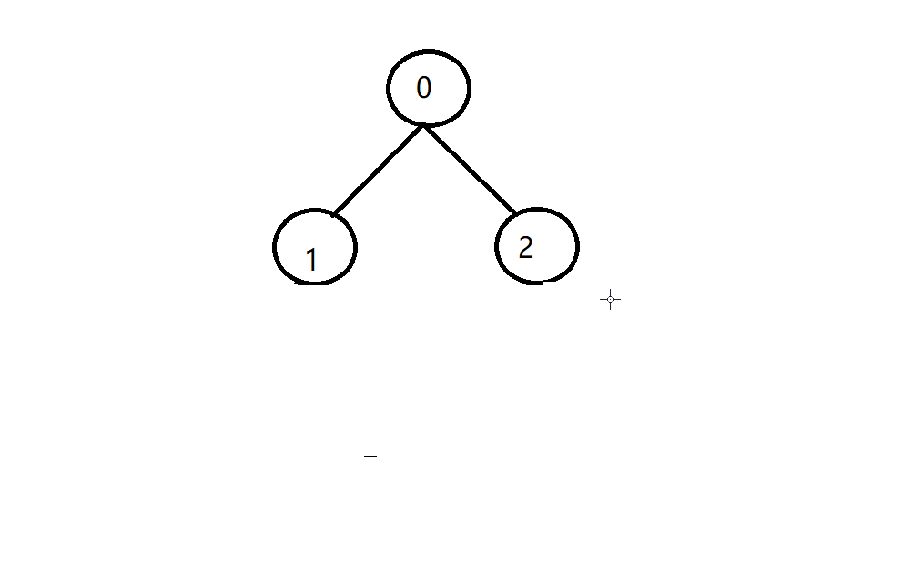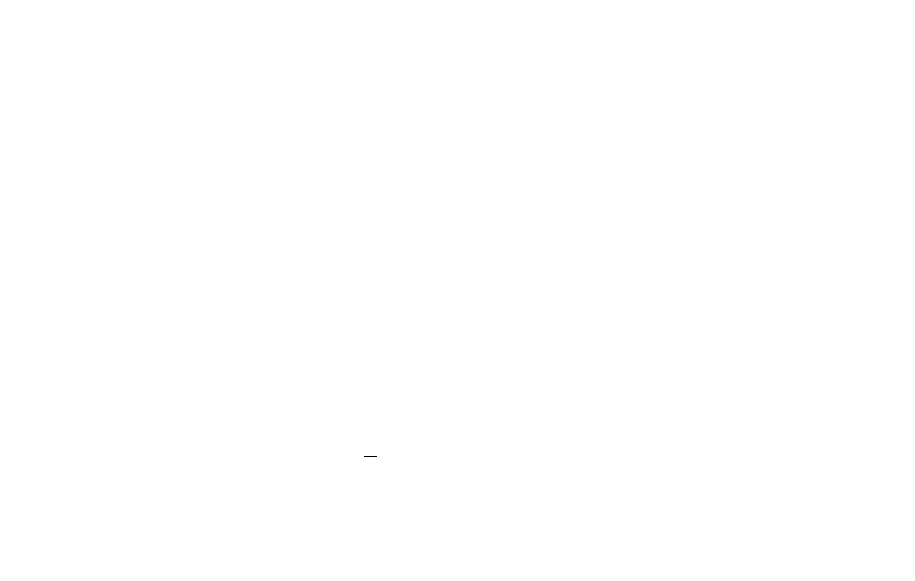
3. 空树与只有根节点的树

3.3 二叉树的性质

1. 根节点的层数为1，非空二叉树的第i层最多有2^i-1个节点

   • i为0即空树，0个节点

2. 只有根节点的二叉树深度为1，而深度为K的二叉树的最大节点数为2^k - 1个

   • k为0即空树，0个节点

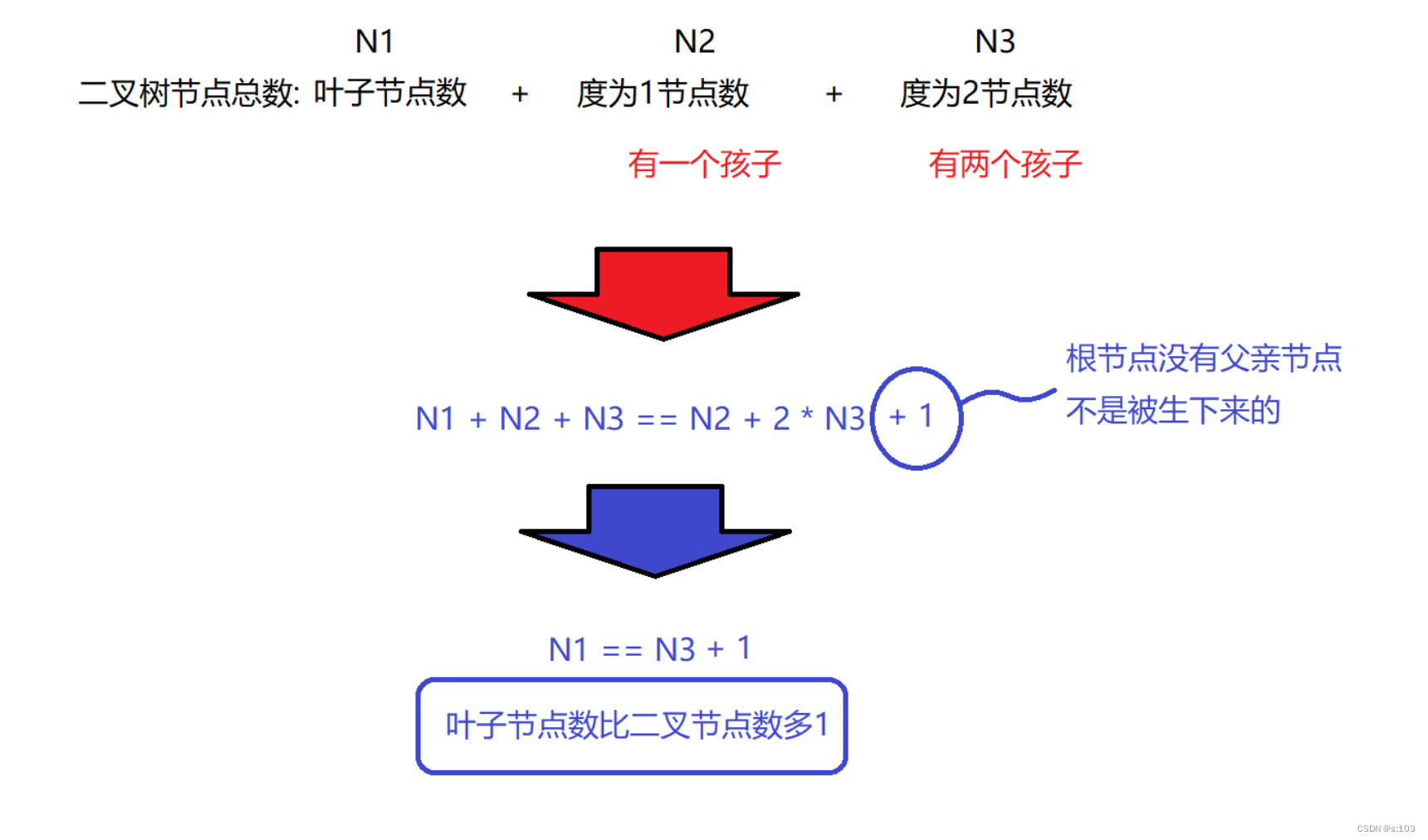
3. 任何一颗二叉树，度为2的节点比叶子节点少一个

4. 具有n个节点的完全二叉树的深度 k = log₂(n + 1)（向上取整）

5. 具有n个节点的完全二叉树，根节点 0 开始编号（从上到下，从左到右）

   • 父亲节点编号的（2 * i + 1 或者 2 * i + 2），【i代表父亲节点的编号】
     • 2 * i + 1 为左孩子序号
     • 2 * i + 2 为右孩子序号
   • 孩子节点编号的（(i - 1) / 2），【i代表孩子节点的编号】
   • 跟节点从1开始，有所不同

3.3.1 证明第三点

3.3.2 证明第四点

设深度为k，跟此完全二叉树深度一样的二叉树的完全二叉树都满足：

1. n <= 2^k - 1
2. n > 2^k-1 - 1

所以 k - 1 < log₂(n + 1) <= k

log₂(n + 1)向上取整后就是k

• 3.1 ==> 4,

• 3.9 ==> 4

• 满二叉树刚好取到k

4. 二叉树遍历

4.1 定义类二叉树MyBinaryTree

• TreeNode类型的根节点对象

public class MyBinaryTree {static class TreeNode{char val;TreeNode left;TreeNode right;public TreeNode(char val) {this.val = val;}TreeNode() {}}TreeNode root;
}

• 内部类TreeNode（树的节点）：

1. 节点存储值value
2. 左子树：left
3. 右子树：right
4. 构造方法~

static class TreeNode{char val;TreeNode left;TreeNode right;public TreeNode(char val) {this.val = val;}TreeNode() {}
}

4.2 示例二叉树暴力创建

public void create(){this.root = new TreeNode('a');this.root.left = new TreeNode('b');this.root.left.left = new TreeNode('d');this.root.left.left.left = new TreeNode('h');this.root.left.right = new TreeNode('e');this.root.right = new TreeNode('c');this.root.right.left = new TreeNode('f');this.root.right.right = new TreeNode('g');
}

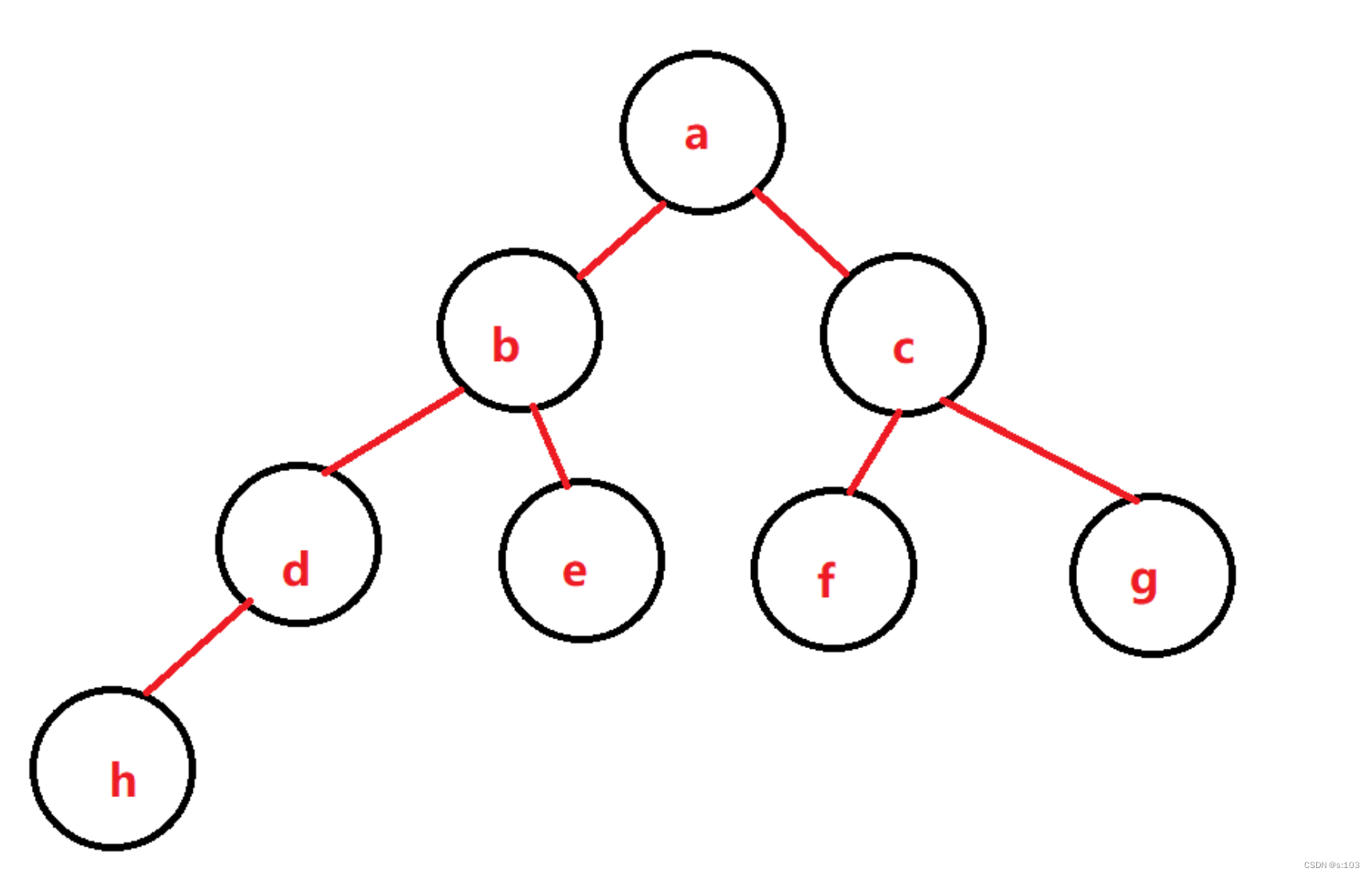
4.3 三种遍历方式（递归法）

4.3.1 前序遍历

//遍历利用了左右都为二叉树的原理！
void preOrder(TreeNode root) {if(root == null) {return;}else {System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}
}

• 递归的核心就是

  1. 宏观整体化思想
  2. 细节处理递归出口

  假设我们这个方法已经设计出来了，那么这个方法也可以遍历左子树和右子树

  • 如果根节点为null不遍历~

前序遍历：先打印根节点，再打印左子树，再打印右子树

那么就有：

• 调用左右子树打印之前，打印根节点数值就OK啦~

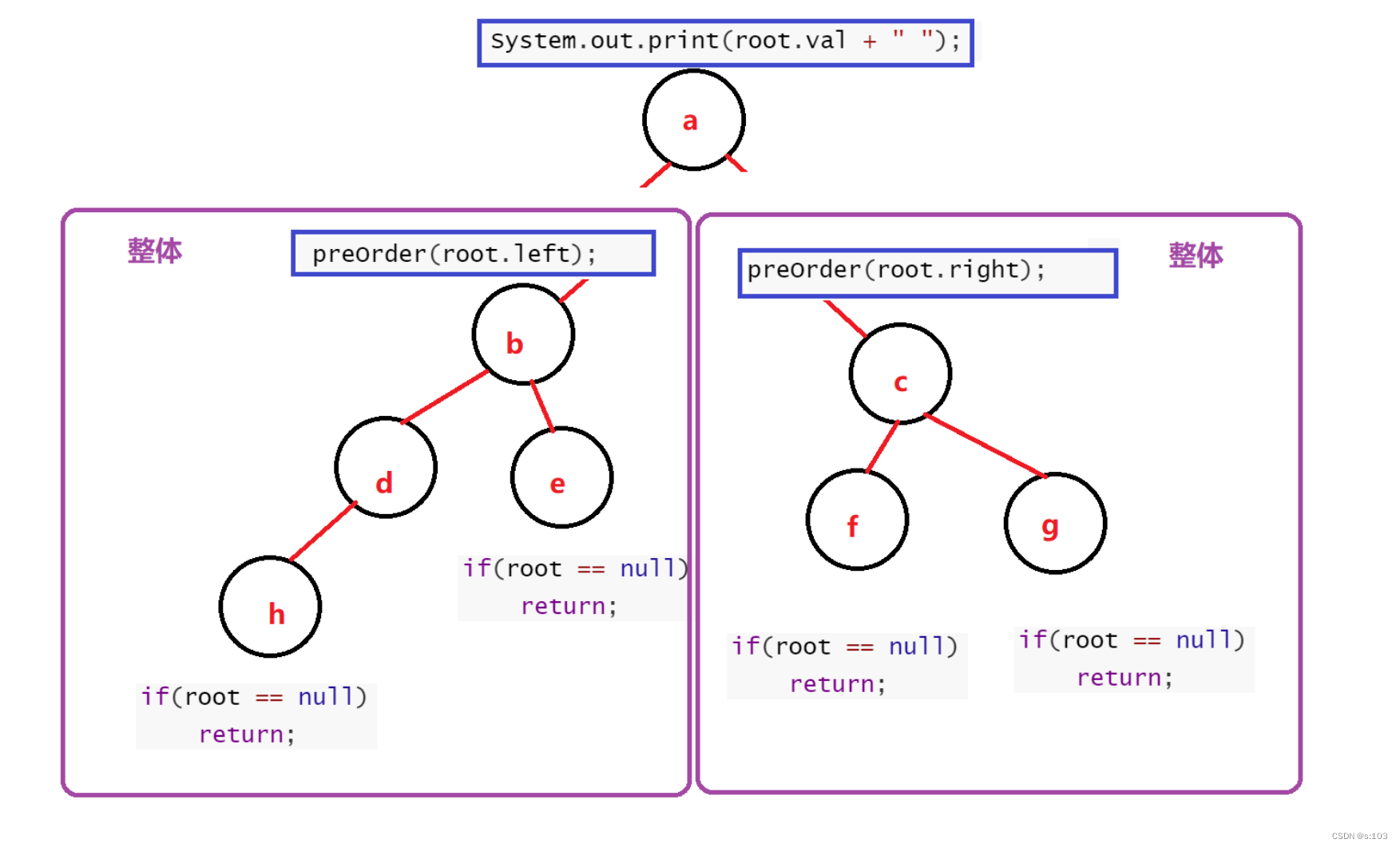
细节分析：

1. 一路到底（最左下端）

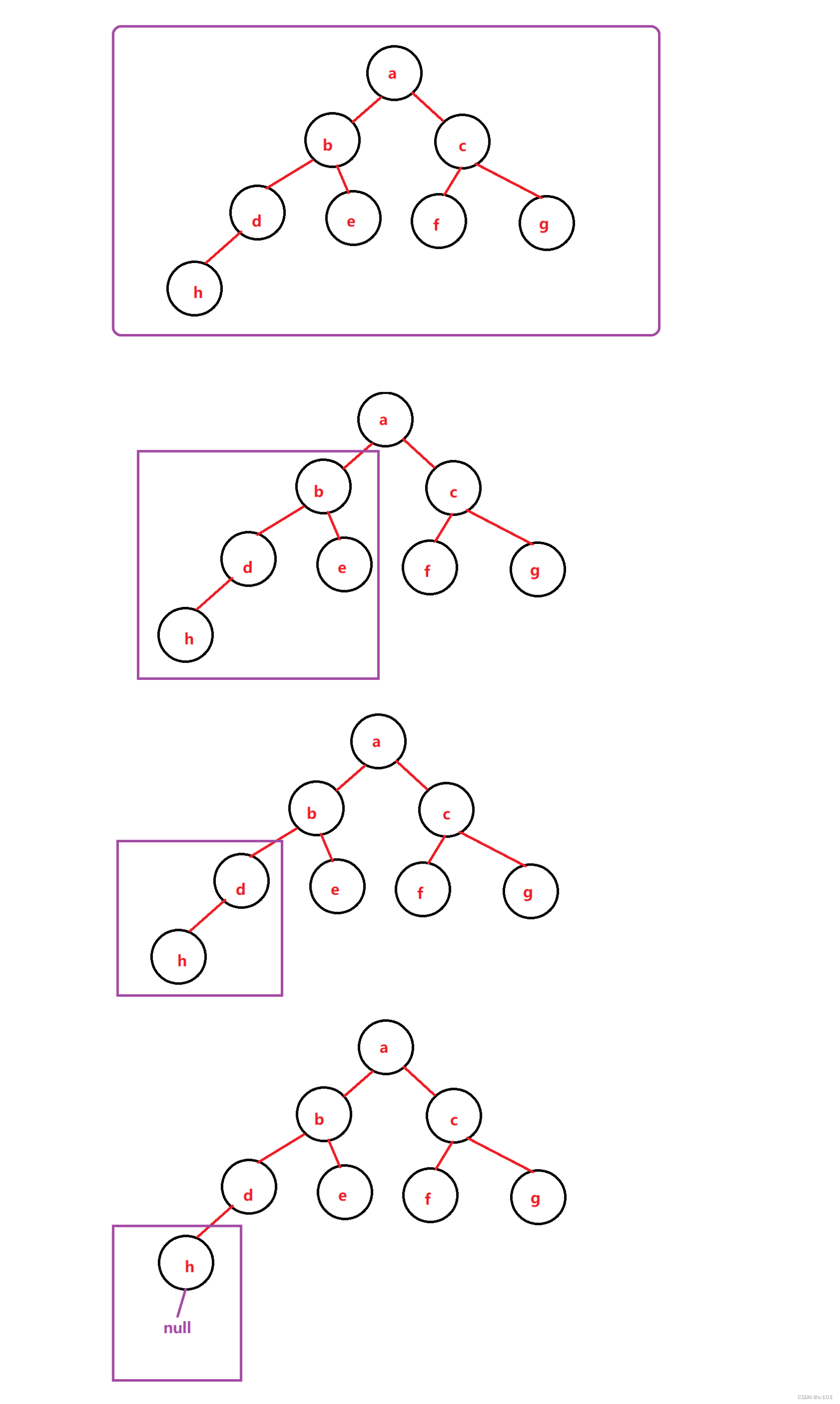
2. 回溯到上一个节点，走右分支，以此类推

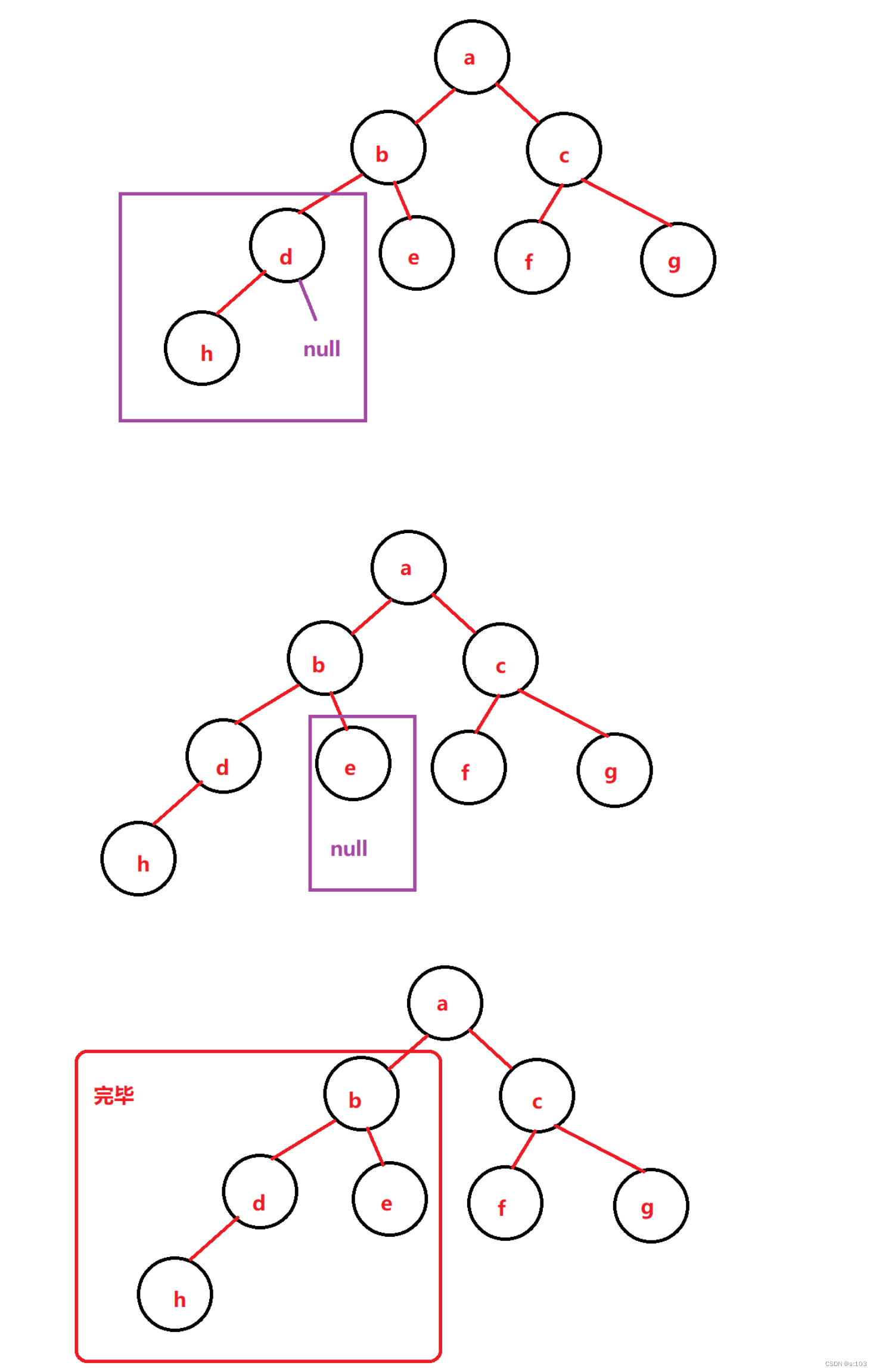
3. 回到最初的方法，走右大子树

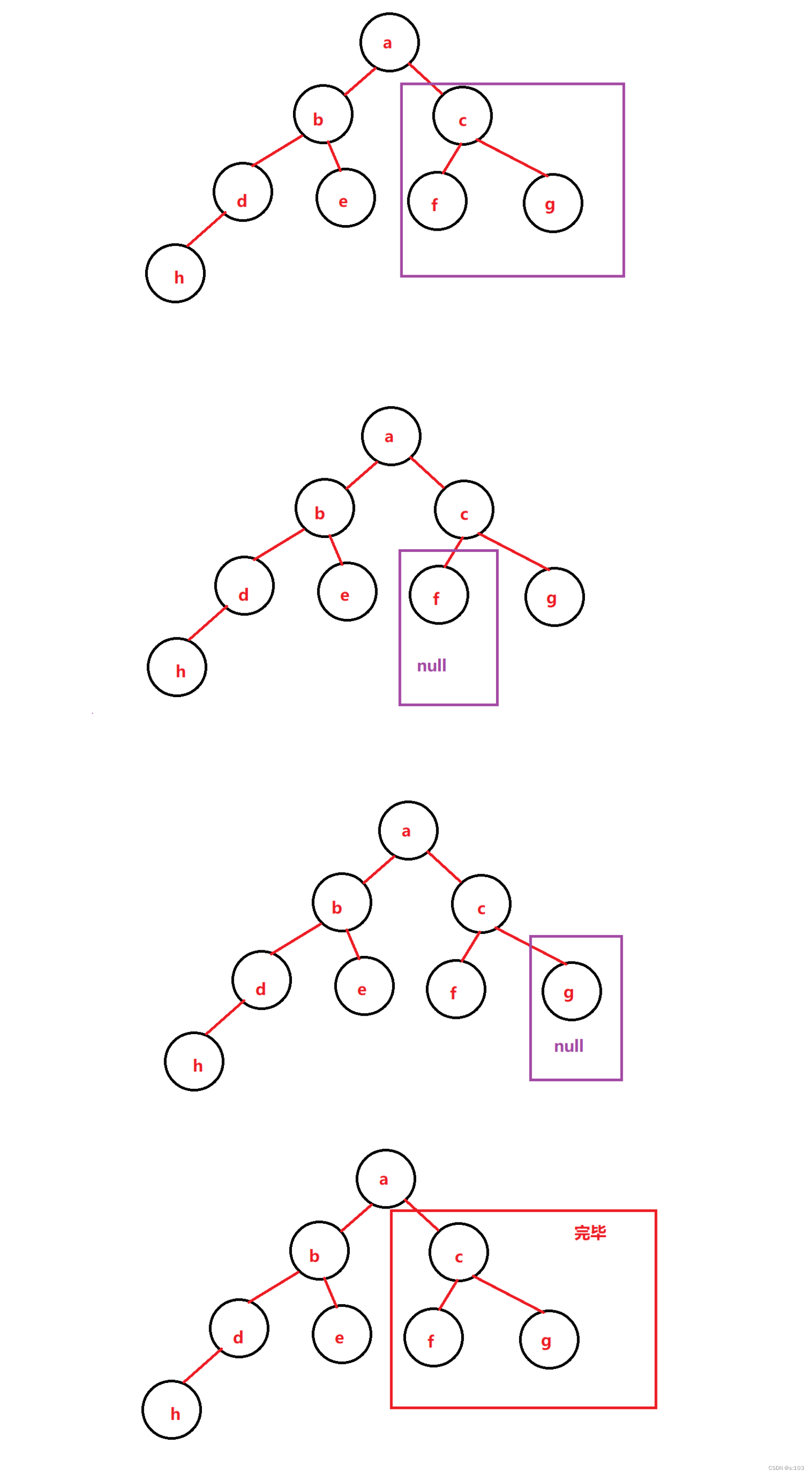
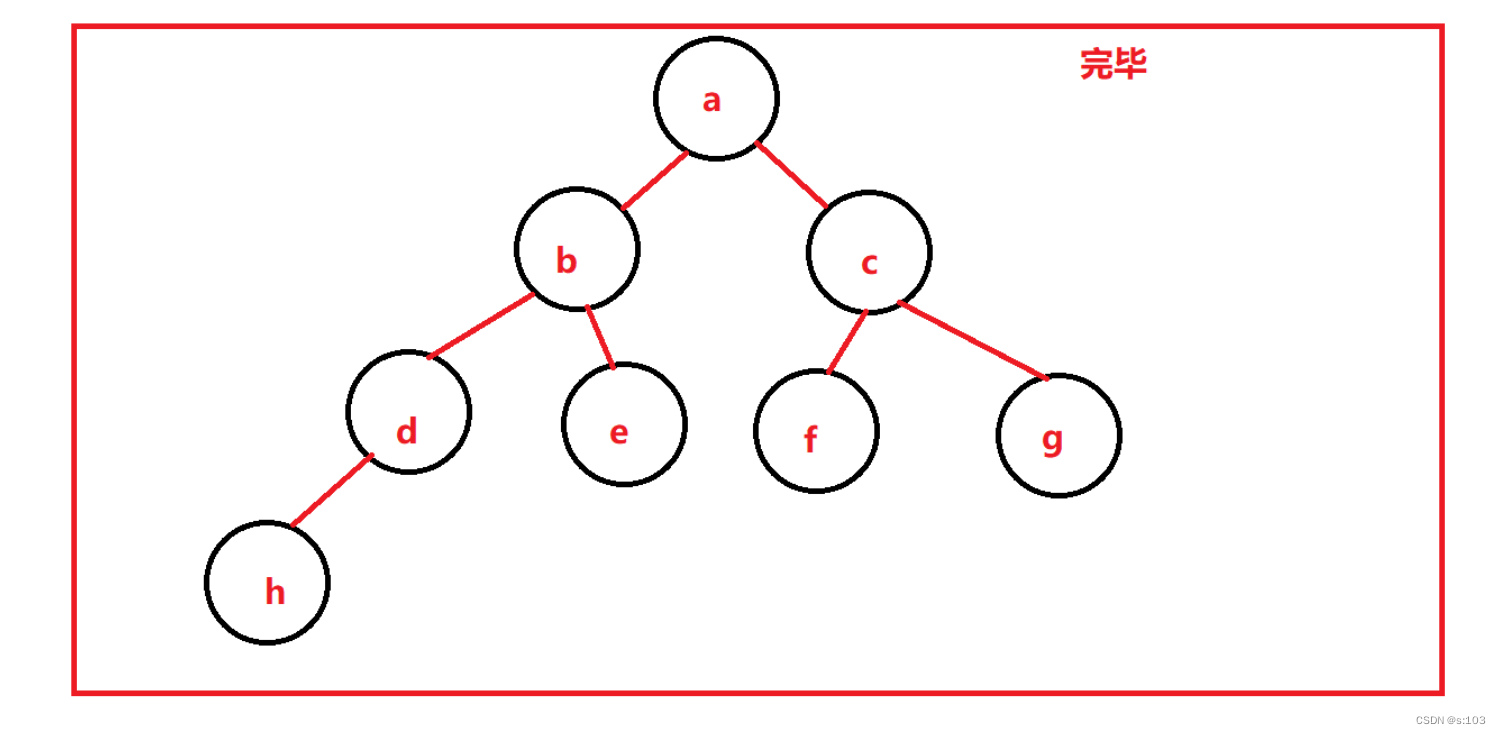
4. 回归初始方法，遍历完毕

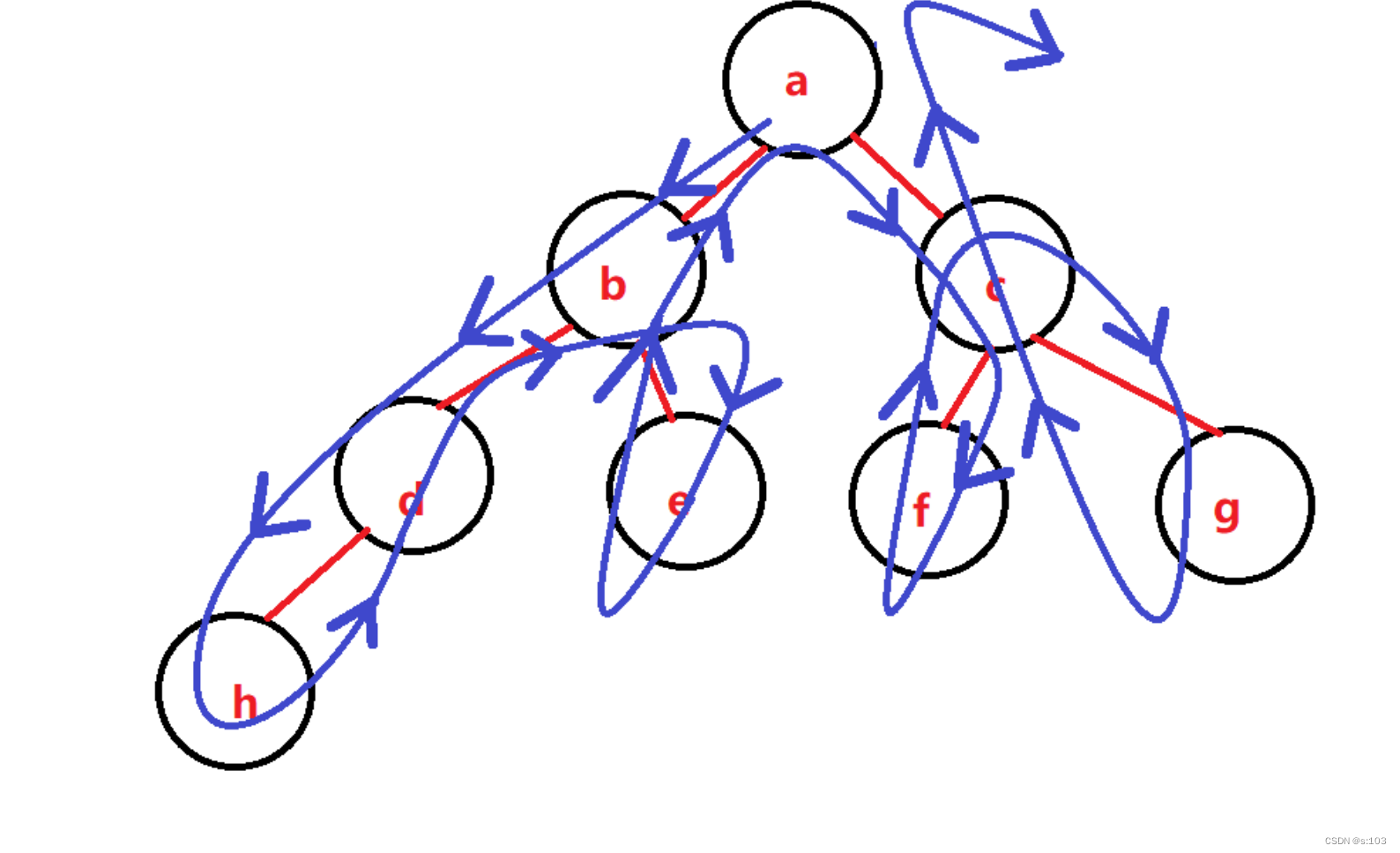
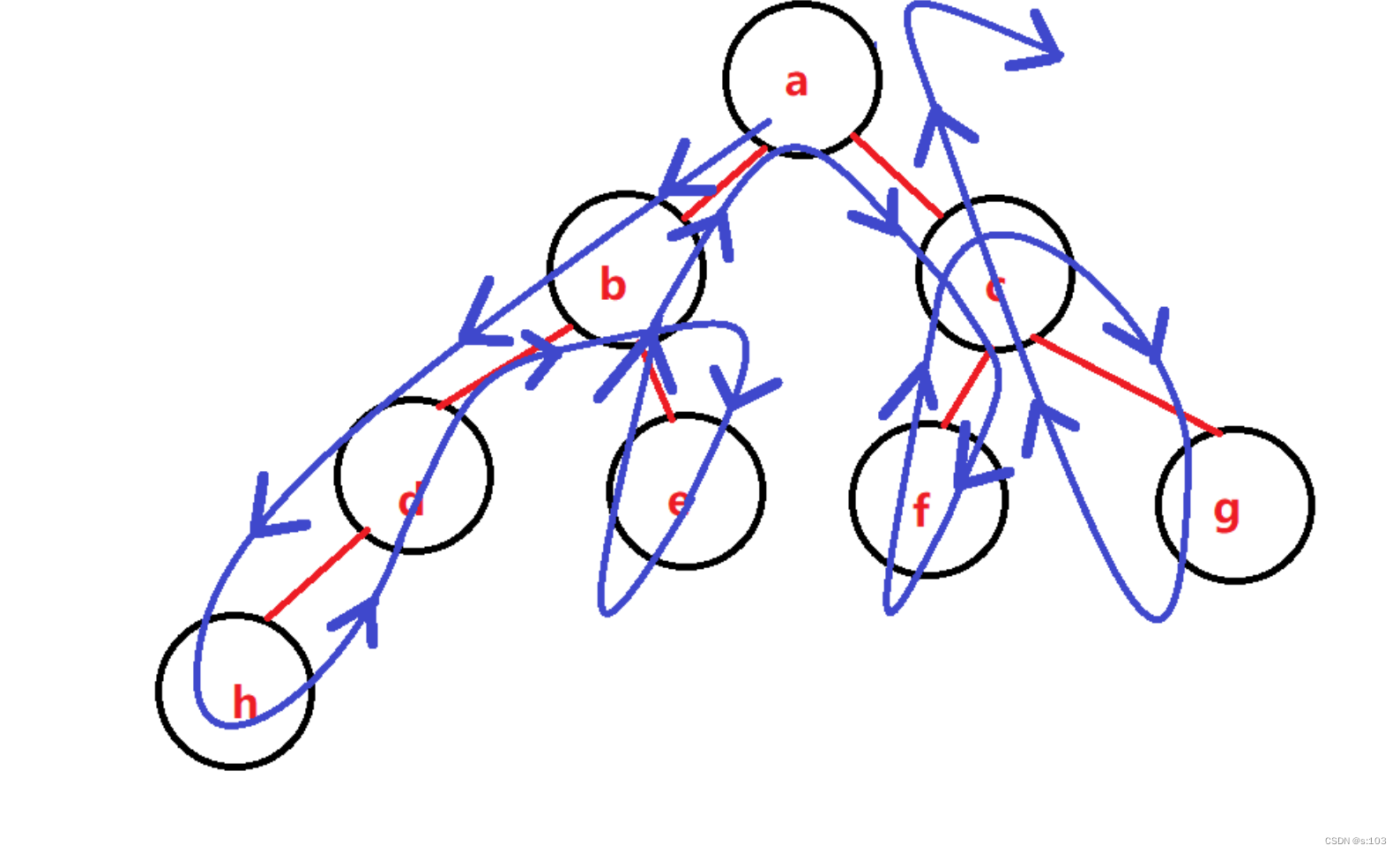
二叉树遍历路线：

• 特别重要！一般都是这样走的！

4.3.2 中序遍历

void inOrder(TreeNode root) {if(root == null) {return;}else {inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}
}

中序遍历：先打印左子树，再打印根节点，再打印右子树

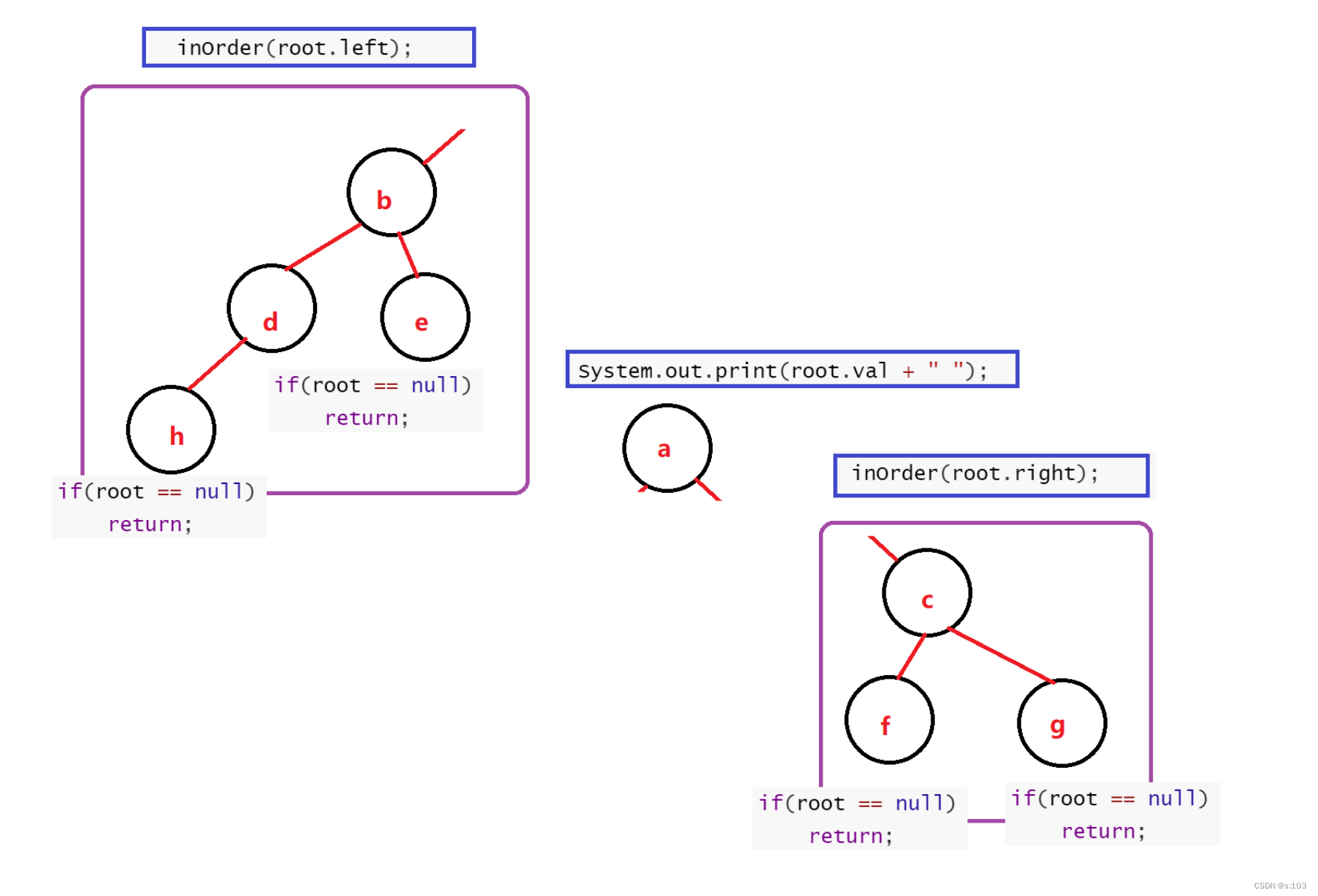
• 线路是一样的：

4.3.3 后序遍历

void postOrder(TreeNode root) {if(root == null) {return;}else {postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}
}

后序遍历，先打印左子树，再打印右子树，再打印根节点

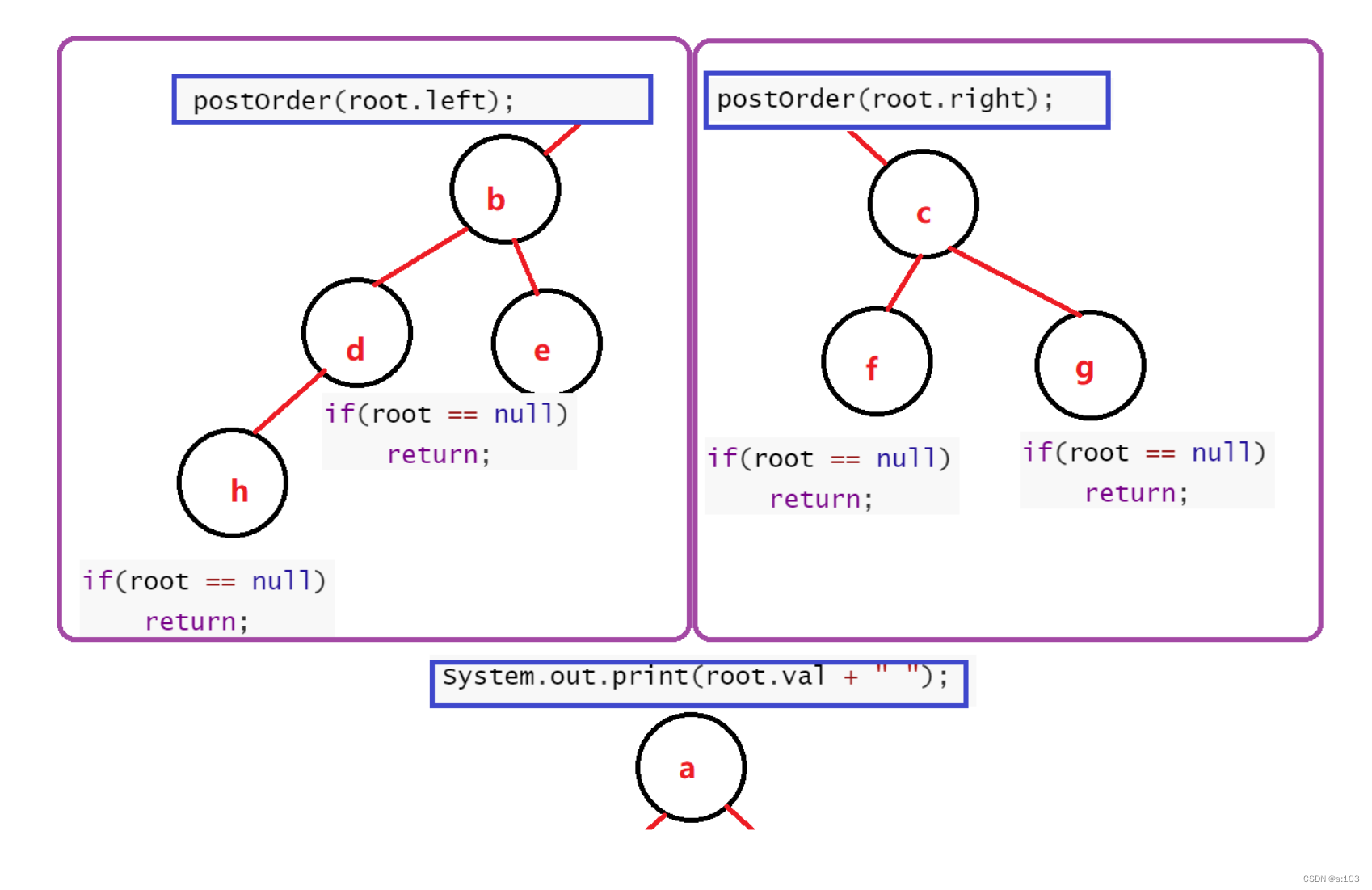
• 线路是一样的：

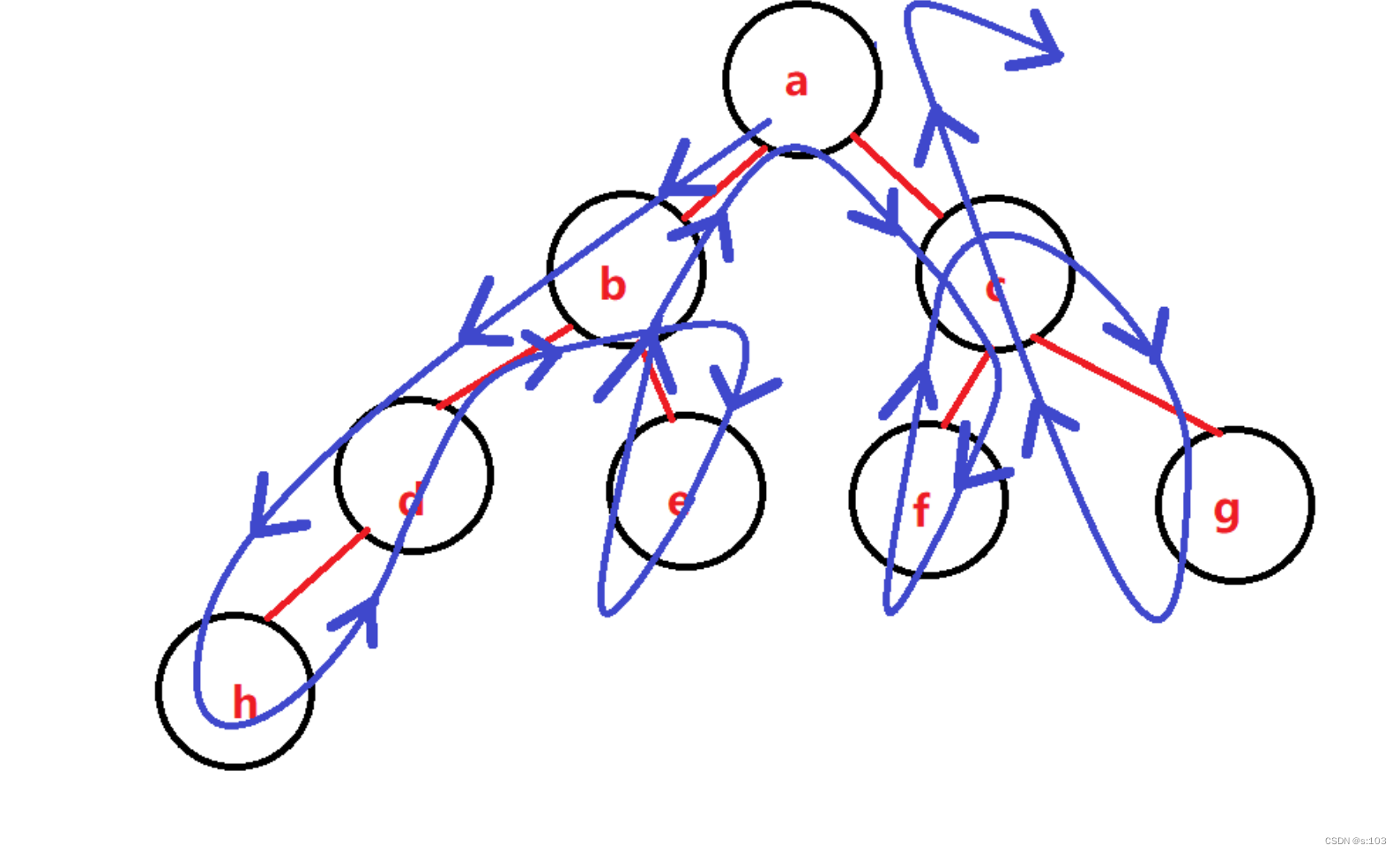
文章到此结束！谢谢观看
可以叫我 小马，我可能写的不好或者有错误，但是一起加油鸭🦆！

如果你能理解这个遍历路线，掌握三种遍历模式，你一定是一个学习二叉树的好手！

后面的题也能轻松应对！

后续会更新更多二叉树知识，敬请期待！