证明电压电流相位差的余弦值和功率因数相等

有没有搞懂？别急，我来用最通俗的语言给你“翻译”一下这个高深的问题！

首先，我们要知道两个主角：“电压电流相位差的余弦值”和“功率因数”。简单概括，相位差就是电压和电流之间的时间差，用θ表示；而功率因数则是用来衡量有多少电能真正被用电设备用来做功的比例。

那这两个看似八竿子打不着的东西为啥能“扯”到一块呢？答案就在下面的推导中！

首先，咱们把电压和电流都表示成正弦函数的形式，就像这样：

电压u(t) = Um * sin(ωt + α)

电流i(t) = Im * sin(ωt + β)

相位差θ就是这两个波形的“时间差”，也就是θ = α - β。

接下来，咱们计算一下瞬时功率p(t)。瞬时功率就是电压和电流的乘积，也就是：

p(t) = u(t) * i(t) = Um * Im * sin(ωt + α) * sin(ωt + β)

这个式子可以用三角恒等式化简一下，最后得到一个包含cosθ和cos(2ωt)的表达式。

关键的一步来了！咱们要计算的是平均功率，也就是有功功率P。由于交流电的频率很高，那些快速变化的cos(2ωt)项在一周期内的平均值为零，所以我们只剩下P = U * I * cosθ。

现在，功率因数cosφ就被定义为有功功率P与视在功率S的比值，也就是：
cosφ = P/S = (U * I * cosθ)/(U * I) = cosθ。

所以，经过一番“折腾”，咱们终于证明了cosθ = cosφ！

概括来讲，，电压和电流的时间差（相位差）和功率因数虽然看起来没啥关系，但通过计算它们的瞬时功率和平均功率，我们发现它们的余弦值其实是“一个模子刻出来的”！这个结论在电力系统中非常重要，因为它可以帮助我们更好地理解和优化电能的使用效率。

再深入思考一下，这个结论还说明了相位差对电能质量的影响。如果相位差太大，意味着功率因数会变低，这会导致供电系统更加“吃力”，需要传输更多的电能才能满足实际需求。这就是为什么工程师们总是想方设法减小相位差的原因啦！

证明：“电压电流相位差的余弦值”和“功率因数”相等。

电压电流相位差的余弦值和功率因数相等，这在《电路分析》中给出过结论，但没有给出详细的证明过程。其次，在电气工程师考试中，也会经常遇到。

电压电流相位差：是指电压与电流之间的时间差，用θ表示。

功率因数表示一个负荷所需要的有功功率和视在功率的比值。

即cosφ=P/S，

其中：

P为有功功率

Q为无功功率

S为视在功率：S = U*I

cosφ为功率因数，φ为功率因数角。

下面证明：cosθ= cosφ

1、首先建立数学模型

电压函数：u(t)=Um * sin(ωt+α)，用极坐标表示(Um,∠α)

电流函数：i(t)=Im * sint(ωt+β)，用极坐标表示(Im,∠β)

θ = ∠α- ∠β

电压有效值为U

电流有效置为I

为了便于计算，我们可以将极坐标系顺时针旋转α，得到下图：

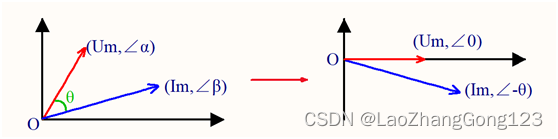
电压函数：u(t)=Um * sin(ωt)，用极坐标表示(Um,∠0)

电流函数：i(t)=Im * sin(ωt-θ)，用极坐标表示(Im,∠-θ)

2、瞬时功率

p(t)=u(t)*i(t)

p(t)=Um * sin(ωt)* Im * sin(ωt-θ)

= Um * Im *[cosθ-cos(2ωt-θ)]/2

= U * I * cosθ- U * I * cos(2ωt-θ)

展开后，瞬时功率为：

p(t)= U * I [cosθ- cosθ* cos(2ωt) - sinθ* sin(2ωt)]

3、有功功率(平均功率)计算

    由于瞬时功率随时间不断变化，工程上应用很不方便,由此引入平均功率。平均功率是指瞬时功率在一个周期内的平均值，又称为有功功率，并用P表示。

令T=2Π/2ω

平均功率：P=(1/T)∫p(t)

P=(1/T)∫