【刷题篇】栈和队列


目录
一.前言🌈
二.有效的括号✨
a.题目
b.题解分析
c.AC代码
三. 用队列实现栈📏
a.题目
b.题解分析(辅助队列法)
c.AC代码(辅助队列法)
d.题解分析(就地存储法)
c.AC代码(就地存储法)
四. 用栈实现队列🍀
a.题目
b.题解分析
c.AC代码
一.前言🌈
各位小友们好久不见,甚是想念!前段时间我们学习了两个重要的数据结构---栈和队列。那么我们的刷题篇也就该提上日程了,本期将带来三道与栈和队列有关的OJ题,它们分别是:
🚀本期的题目有:有效的括号、用队列实现栈、用栈实现队列
注:为了实现方便,本期我们将使用C++来编写代码,利用STL中现有的栈和队列进行实现。
二.有效的括号✨
a.题目

b.题解分析
我们知道,在我们编写的C程序中,会存在着小括号( )、中括号[ ]以及大括号{ },它们总是成对出现且匹配的,满足这个特点的一组括号我们就称它有效。例如{ ( ) [ ] }就是一组匹配的括号,而{ ( [ ) } ] 就不是一组匹配的括号。我们可以发现一个现象,从左往右开始第一个右括号 其前一个括号 必须是与之对应的左括号,否则这组括号就不匹配
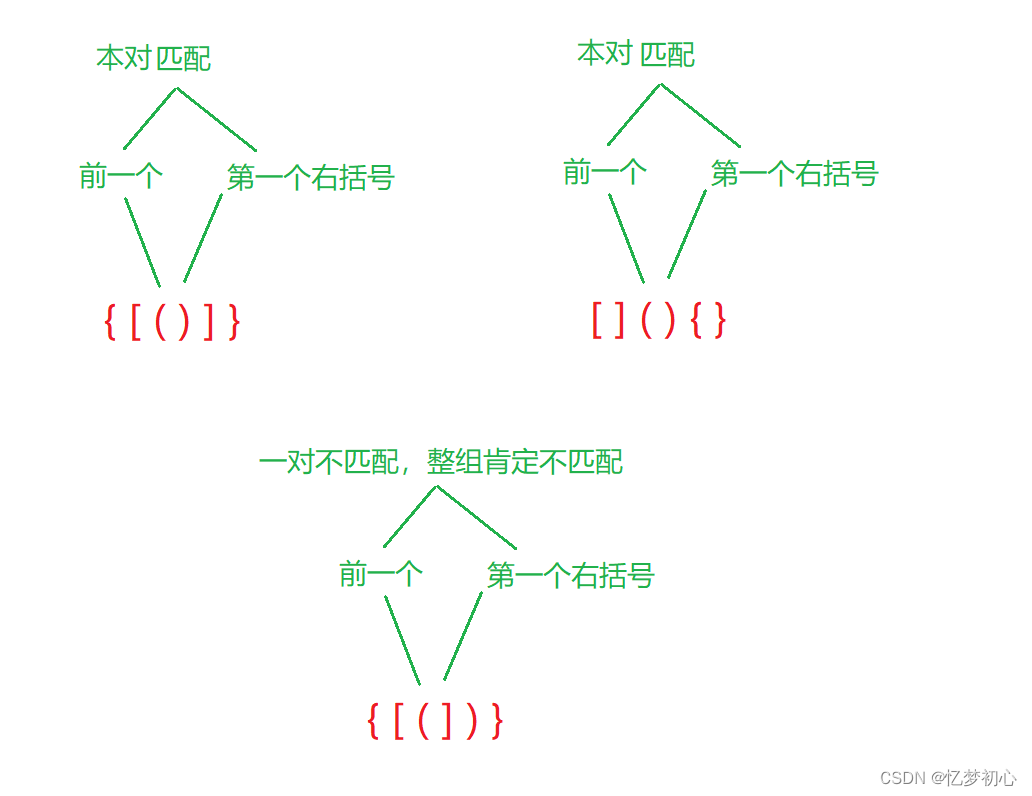
而如果本对括号匹配,我们就可以将本对括号移除,进行下一对括号的判断,直到所有括号都成功匹配,说明本组括号是有效的。如果在这个过程中出现一次不匹配,那就说明本组括号无效。


有了以上思路,那究竟要选择什么合适的数据结构来存放我们的括号呢?
我们自然而然的会想到栈,因为无论是判断是否匹配,移除匹配的括号,我们都只是在其中一端进行操作的。
当我们的指针遇到左括号的时候,我们进行入栈操作。当遇到右括号时,我们就和栈顶的左括号进行比较,如果匹配,则pop出栈,移除匹配的括号;如果不匹配,则直接返回false。依次反复直到遍历完整个字符串。
c.AC代码
class Solution {//存放括号的栈stack<char> sta;
public:bool isValid(string s){//遍历字符串for (int i = 0; i < s.size(); i++){char c = s.at(i);switch (c){case '(':case '[':case '{':sta.push(c);//左括号入栈break;case ')':case ']':case '}':if(sta.empty()) //括号栈为空,匹配失败{return false;}if ((c==')' && sta.top() != '(')||(c==']' && sta.top() != '[')||(c=='}' && sta.top() != '{')){return false; //匹配失败}else{sta.pop();//成功,将匹配成功的左括号出栈}break;default://cout << "输入的字符串有误" << endl;return false;break;}}//遍历完毕,判断括号栈中还有没有剩余的括号if (sta.empty())//为空{return true;}else//不为空,说明左括号多了,匹配失败{return false;}}};三. 用队列实现栈📏
a.题目

b.题解分析(辅助队列法)
本题要求我们用队列来模拟栈。由于队列的特性是先进先出,栈的特性是后进先出,因此我们需要模拟的栈的栈顶实际上是队尾,我们需要在队尾进行一系列操作。特别是出栈,要先将队列前面的元素全部出队后才能执行。

显然前面的元素我们不能直接无视,在它们出队的同时我们要将他们存放起来,以供下次使用。那么我们要怎样存储呢?这里有两个方案:辅助空间存储和就地存储。
我们先来看看辅助空间存储,我们可以再使用一个辅助的队列来存放队尾前面的元素,由于队列先进先出的特性,每个元素的顺序都将保持一致。当我们进行入栈时就入到不为空的队列;进行出栈时将不为空的队列的前n-1个元素移到为空的队列中,然后将剩下的一个元素pop掉。动态演示如下:

c.AC代码(辅助队列法)
class MyStack {queue<int> q1;queue<int> q2;
public:MyStack() {}//入栈void push(int x) {//从不为空的队列放入数据if (!q1.empty()){q1.push(x);}else{q2.push(x);}}//出栈int pop() {if (q1.empty()){swap(q1, q2);}//将前几个元素转移到为空的队列中while (q1.size() > 1){q2.push(q1.front());q1.pop();}int ret = q1.front();q1.pop(); //移除栈顶元素return ret;}//求栈顶元素int top() {//栈顶所在位置即为队尾,直接访问即可if(!q1.empty()){return q1.back();}else{return q2.back();}}//判空bool empty() {//两个队列都为空说明栈为空return q1.empty() && q2.empty();}
};d.题解分析(就地存储法)
上面我们采用了一个辅助队列来进行解题,实际上我们也可以只使用一个队列。出栈的时候只需将前n-1个元素同时出队并再次入队,此时队头元素即为我们的栈顶元素,我们再将其pop,这样依然可以保证原有顺序不变。动态演示如下:

c.AC代码(就地存储法)
class MyStack {queue<int> q1;
public:MyStack() {}//入栈void push(int x) {//放入数据,入队q1.push(x);}//出栈int pop() {//记录当前共有几个元素int count=q1.size();//将前面count-1个元素出队并入队while(count > 1){int val=q1.front();q1.pop();q1.push(val);count--;}//将此时的队头,即栈顶元素出队int ret=q1.front();q1.pop();return ret;}//求栈顶元素int top() {//栈顶元素就是队尾元素return q1.back();}//判空bool empty() {//队列为空说明栈为空return q1.empty();}
};四. 用栈实现队列🍀
a.题目

b.题解分析
本题和上一题基本上一样,区别就是我们这次模拟的是队列。由于队列是先进先出,栈是后进先出,因此我们在模拟出队时依旧要将前n个元素先进行出栈。

那么,我们要怎样将移除的前n-1个元素存放起来呢,可以就地存储吗?
答案是不行的。由于栈是先进先出,出栈和入栈是在同一端进行的,出栈的同时入栈相当于啥也没做。因此我们只能再使用一个栈进行辅助。

我们可以设计两个栈,一个栈存储入队的元素(input),另一个栈用于出队(output)。当进行入栈时,则往input入栈;当进行出栈时,如果ouput为空,则先将input中的元素压入output中,此时output的栈顶元素恰好就是队头元素,然后出栈即可,如果不为空,则直接出栈。动态演示如下:
c.AC代码
class MyQueue {stack<int> input;stack<int> output;
public:MyQueue() {}//入队void push(int x){//往input入栈input.push(x);}//出队int pop(){//output为空,先将input数据移入if (output.empty()){while (!input.empty()){int val = input.top();input.pop();output.push(val);}}//此时output栈顶元素即为队头元素,出栈int ret = output.top();output.pop();return ret;}//求队头元素int peek(){//output为空,先将input数据移入if (output.empty()){while (!input.empty()){int val = input.top();input.pop();output.push(val);}}//栈顶元素即为队头元素int ret = output.top();return ret;}//判空bool empty(){//两个栈都为空说明队列为空return input.empty() && output.empty();}
};以上,就是本期的全部内容啦🌸
制作不易,能否点个赞再走呢🙏