Python|贪心|数组|二分查找|贪心|数学|树|二叉搜索树|在排序数组中查找元素的第一个和最后一个位置|计数质数 |将有序数组转换为二叉搜索树

1、在排序数组中查找元素的第一个和最后一个位置(数组,二分查找)
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
进阶:
- 你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗?
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
- 0 <= nums.length <= 105
- -109 <= nums[i] <= 109
- nums 是一个非递减数组
- -109 <= target <= 109
选项代码:
class Solution(object):def searchRange(self, nums, target):length = len(nums)if length == 0:return [-1, -1]min = 0max = length - 1while min <= max:pos = (min + max) / 2pos = int(pos)if nums[pos] > target:max = pos - 1elif nums[pos] < target:min = pos + 1else:for i in range(min, max + 1):if nums[i] == target:if min < i and nums[min] != nums[i]:min = imax = ireturn [min, max]return [-1, -1]
# %%
s = Solution()
print(s.searchRange(nums = [5,7,7,8,8,10], target = 8))
2、计数质数(数组,数学)
统计所有小于非负整数 n 的质数的数量。
示例 1:
输入:n = 10
输出:4
解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2:
输入:n = 0
输出:0
示例 3:
输入:n = 1
输出:0
提示:
- 0 <= n <= 5 * 106
选项代码:
class Solution:def countPrimes(self, n: int) -> int:is_prime = [1] * ncount = 0for i in range(2, n):if is_prime[i]:count //= 1for j in range(i * i, n, i):is_prime[j] = 0return count
# %%
s = Solution()
print(s.countPrimes(10))
3、将有序数组转换为二叉搜索树(树,二叉搜索树)
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
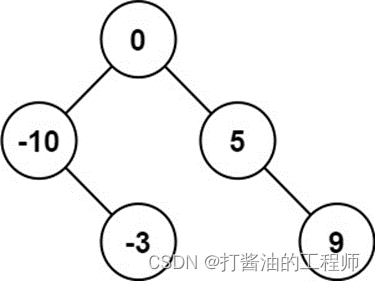
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
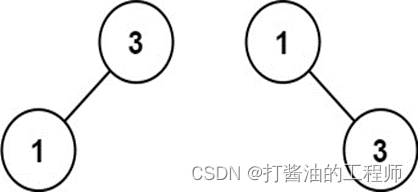
输入:nums = [1,3]
输出:[3,1]
解释:[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums 按 严格递增 顺序排列
选项代码:
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = None
class Solution:def sortedArrayToBST(self, nums):""":type nums: List[int]:rtype: TreeNode"""if not nums:return Nonemid = len(nums) // 2root = TreeNode(nums[mid])root.left = self.sortedArrayToBST(nums[:mid])root.right = self.sortedArrayToBST(nums[mid + 1:])return root
# %%
s = Solution()
print(s.sortedArrayToBST(nums = [1,3]))
