【LeetCode: 337. 打家劫舍 III | 暴力递归=＞记忆化搜索=＞动态规划 | 树形dp】

🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀
🌲 越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样✨
🌲 作者简介：硕风和炜，CSDN-Java领域新星创作者🏆，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎
🌲 恭喜你发现一枚宝藏博主,赶快收入囊中吧🌻
🌲 人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？🎯🎯

🚗 知识回顾 ## 题目回顾

大家再看这道题目之前，可以先去看一下我之前写过的一篇关于打家窃舍算法题的博客，再看这个这更容易理解了。
博客的地址放到这里了，可以先去学习一下这到题目。

• 【LeetCode: 剑指 Offer II 089. 房屋偷盗（打家窃舍） | 暴力递归=＞记忆化搜索=＞动态规划】
• 【LeetCode: 剑指 Offer II 090. 环形房屋偷盗（打家窃舍） | 暴力递归=＞记忆化搜索=＞动态规划】

🚩 题目链接

• 337. 打家劫舍 III

⛲ 题目描述

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

提示：

树的节点数在 [1, 104] 范围内
0 <= Node.val <= 104

示例1:

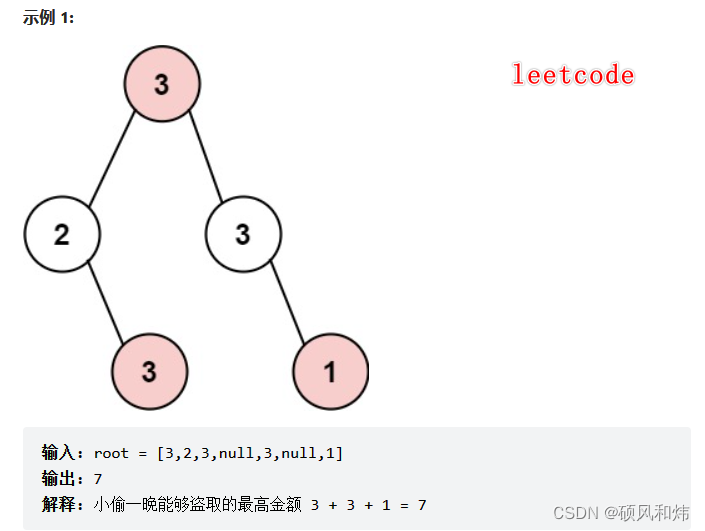
示例2:

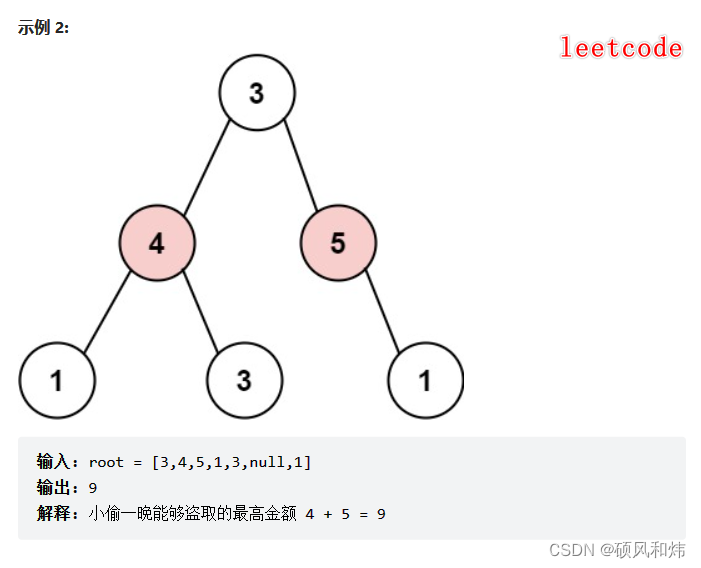
🌟 求解思路&实现代码&运行结果

⚡ 暴力递归

🥦 求解思路

1. 核心思路和我们之前【打家劫舍】系列的题目求解思路是一样的，做这道题之前可以先看一下之前的俩到题目；
2. 这道题目不同的是在树上进行偷取的决策，来到树上的每一个位置的节点，我们可以选择偷取，也可以选择不偷取；
3. 因为当前位置是否偷取是影响后续的状态的，所以我们在设计递归的时候需要一个变量flag来标记当前位置是否选择过，如果当前位置是选择的，那么左右子树是不能进行选择的；如果当前是没有选择过的，那么此时左子树可以进行【选择，不选择】的决策，同样，右子树也是可以进行【选择，不选择】的决策。根据乘法原理，我们可以俩俩组合，最后可以组成四种情况，我们在这四种情况中取得最大的值返回即可。
4. 具体的代码实现如下所示。

🥦 实现代码

/* Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int rob(TreeNode root) {if(root==null) return 0;return Math.max(process(root,true),process(root,false));}public int process(TreeNode root,boolean steal){if(root==null) return 0;if(steal==true){return process(root.left,false)+process(root.right,false)+root.val;}else{int p1=process(root.left,true)+process(root.right,true);int p2=process(root.left,true)+process(root.right,false);int p3=process(root.left,false)+process(root.right,true);int p4=process(root.left,false)+process(root.right,false);return Math.max(Math.max(p1,p2),Math.max(p3,p4));}}
}

🥦 运行结果

⚡ 记忆化搜索

🥦 求解思路

1. 根据我们递归的分析，在递归的过程中会产生重复的子过程，所以我们想到了加一个缓存表，也就是我们的记忆化搜索。

🥦 实现代码

/* Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {private HashMap<String,Integer> map=new HashMap<>();public int rob(TreeNode root) {if(root==null) return 0;return Math.max(process(root,true),process(root,false));}public int process(TreeNode root,boolean steal){if(root==null) return 0;if(map.containsKey(root+"-"+steal)) return map.get(root+"-"+steal);if(steal==true){map.put(root.val+"-"+steal,process(root.left,false)+process(root.right,false)+root.val);return process(root.left,false)+process(root.right,false)+root.val;}else{int p1=process(root.left,true)+process(root.right,true);int p2=process(root.left,true)+process(root.right,false);int p3=process(root.left,false)+process(root.right,true);int p4=process(root.left,false)+process(root.right,false);map.put(root+"-"+steal,Math.max(Math.max(p1,p2),Math.max(p3,p4)));return Math.max(Math.max(p1,p2),Math.max(p3,p4));}}
}

🥦 运行结果

⚡ 动态规划

🥦 求解思路

1. 因为该题目是树形dp，所以我们最后就不改成递推的形式了，我们在原来的递归和记忆化缓存思路上进一步优化我们的递归，让其成为解决所有树形dp的模板；
2. 怎么改呢？我们先来分析一下，首先我们需要将所有可能展开，展开的情况就是一颗二叉树；
3. 那么每一个节点的值是什么呢？每一个节点的值是左右子树节点偷或者不偷的值(注意:这也就是我们设计递归的返回值)；
4. 所以我们可以先根据后序遍历先遍历树，然后到了每一个根节点进行结果的收集。
5. 怎么收集呢？我们开辟一个大小为2的数组，下标0表示不偷，下标1表示偷取，将答案收集到每一个数组中，逐层返回。

🥦 实现代码

注意:此处实现的代码0表示不偷，1表示偷；上面思路中true表示偷，false表示不偷

class Solution {public int rob(TreeNode root) {if(root==null) return 0;int[] ans=process(root);return Math.max(ans[0],ans[1]);}public int[] process(TreeNode root){if(root==null) return new int[]{0,0};int[] left=process(root.left);int[] right=process(root.right);int[] dp=new int[2];dp[0]=Math.max(left[0],left[1])+Math.max(right[0],right[1]);dp[1]=root.val+left[0]+right[0];return dp;}
}

🥦 运行结果

💬 共勉

最后，我想送给大家一句一直激励我的座右铭，希望可以与大家共勉！