Mit6.006-lecture07-BinaryTrees2AVL

一、上次与今日目标
| 序列数据结构 | 操作,最坏情形O | ||||
| 容器(container) | 静态(static) | 动态(dynamic) | |||
| build(x) | get_at(i) set_at(i, x) |
insert_first(x) delete_first() |
insert_last(x) delete_last() |
insert_at(i, x) delete_at(i) |
|
| 二叉树 | n | h | h | h | h |
| AVL树 | n | logn | logn | logn | logn |
| 集合数据结构 | 操作,最坏情形O | ||||
| 容器(container) | 静态(static) | 动态(dynamic) | 顺序(order) | ||
| build(X) | find(k) | insert(x) delete(k) |
find_min() find_max() |
find_prev(k) find_next(k) |
|
| 二叉树 | nlogn | h | h | h | h |
| AVL树 | nlogn | logn | logn | logn | logn |
二、高度平衡
-
如何维持高度h=O(logn)h=\\mathcal{O}(\\log n)h=O(logn),n为树中节点的数量
-
在动态操作中维持树的高度为O(logn)\\mathcal{O}(\\log n)O(logn)的二叉树称为平衡的
-
有多种平衡方式(红黑树、伸展树SplayTree、2-3Tree)
-
首次提出的平衡方式为AVL树
-
三、旋转(Rotations)
-
需要降低树的高度,而不改变遍历顺序,因此我们表示相同序列的项目
-
保留遍历顺序时,如何改变树的结构?旋转!
图1 rotate_right(<D>) 得到图2、图2 rotate_left(<B>) 得到图2
- 旋转重新链接O(1)\\mathcal{O}(1)O(1)指针更改树结构、维持遍历顺序
四、Rotations Suffice
-
声明:O(n)\\mathcal{O}(n)O(n)次旋转可以转换二叉树为任意其他二叉树(拥有相同遍历顺序)
-
证明:按遍历顺序重复执行最后可能的右旋;结果树为经典的链表。每次旋转最后节点的深度增加1。最终链中最后节点的深度为n−1n-1n−1,因此最多执行n-1次旋转。反向旋转得到目标树
-
通过使用O(n)\\mathcal{O}(n)O(n)次旋转,可以维持高度平衡来完全平衡二叉树,但很慢
-
每次操作,我们将耗时O(logn)\\mathcal{O}(\\log n)O(logn)维持树的平衡
五、AVL树:高度平衡
-
AVL树维持高度平衡(也称作AVL属性)
-
如果左、右子树高度最多相差1,那么节点是高度平衡的
-
让节点的偏斜为右子树高度减左子树高度
-
如果它的偏斜为-1、0、1,那么节点是高度平衡的
-
-
声明:拥有高度平衡节点的二叉树,高度为h=O(logn),比如n=2Ω(h)h=\\mathcal{O}(\\log n),比如n=2^{\\Omega(h)}h=O(logn),比如n=2Ω(h)
-
证明:任意高度为h的树,最少节点F(h)=2Ω(h)F(h)=2^{\\Omega(h)}F(h)=2Ω(h)
F(0)=1,F(1)=2,F(h)=1+F(h-1)+F(h-2) >= 2F(h-2) => F(h)≥2h/2F(h)\\ge2^{h/2}F(h)≥2h/2
-
假设从高度平衡树中添加或删除叶子导致不平衡
-
仅叶子祖先的子树高度改变或歪曲
-
改变高度仅为1,因此倾斜幅度$\\le$2
-
点子:从叶子到根,修复祖先的高度平衡
-
重复地再平衡(高度不平衡的)最低祖先
-
-
本地再平衡:给定二叉树节点<B>:
-
倾斜为2且
-
<B>子树的每个其他节点是高度平衡的,
-
<B>的子树可以通过一次或2次旋转达到高度平衡
-
(之后,<B>的高度将等于或小于之前的高度)
-
-
证明:
-
因为B的倾斜是2,所以<B>的右子树<F>存在
-
case1:<F>的倾斜是0、或case2:<F>的倾斜是1
- 在<B>上执行左旋
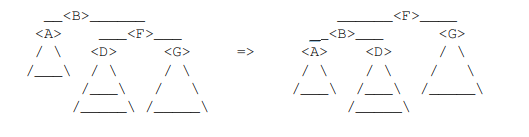
- 让h=height(<A>),那么height(<G>)=h+1,并且height(<D>)是h+1(case1)或h(case2)
- 旋转后:
- <B>的倾斜要么是1(case1),要么是0(case2),因此<B>是高度平衡的
- <F>的倾斜是-1,因此<F>是高度平衡的
- <B>的高度之前是h+3,之后为h+3(case1)、h+2(case2)
-
case3:<F>的倾斜是-1,因此<F>的左子节点<D>存在
- 在<F>上执行右旋,在<B>上执行左旋
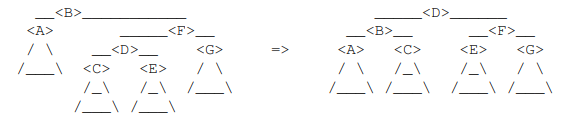
- 让h=height(<A>)。那么height(<G>)=h,height(<C>)和height(<E>)是h或h-1
- 旋转后:
- <B>的倾斜是0或-1,因此<B>的高度是平衡的
- <F>的倾斜是0或1,因此<F>的高度是平衡的
- <D>的倾斜是0,因此D是高度平衡的
- <B>的高度之前是h+3,那么之后是h+2
-
-
全局再平衡:从高度平衡树T中添加或删除一个叶子生成树T’。然后T‘可以使用至多O(logn)\\mathcal{O}(\\log n)O(logn)次旋转转换成一个高度平衡树T’’
-
证明:
-
仅受影响叶子的祖先,T’比T有不同的高度
-
受影响叶子至多h=O(logn)h=\\mathcal{O}(\\log n)h=O(logn)个祖先(它的子树可能已经改变)
-
让<X>为最低的高度不平衡祖先(倾斜度是2)
-
如果一个叶子加到T:
-
插入增加<X>的高度,因此是不平衡的case2或case3
-
旋转降低子树的高度:旋转后平衡
-
-
如果叶子从T中移除:
-
删除使<X>子节点的高度降低1,并非<X>,因此仅不平衡
-
可能让<X>的高度降低1;
-
-
