目录

前言

一、概念

二、代码实现

1.set

2.reset

3.test

三、位图的应用

前言

我们先来看腾讯曾经的一道面试题：

 

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在

这40亿个数中。

 

常规方法：

1. 遍历，时间复杂度O(N)

2. 排序(O(NlogN))，利用二分查找: logN

这道题如果是不可能用常规方法来解决的，因为存储40亿个整形需要的空间太大了，高达16G。

这种情况，我们就可以用到今天的主角——位图。

 

给定的每个整形只有两种状态：在与不在，我们完全可以通过一个比特位的0和1来记录每个数字在不在。这样大大节省了空间，只需要500MB的空间即可。

一、概念

二、代码实现

底层结构我们用一个vector，容器中存储的类型为char。因为一个char类型占用一个字节，我们将八个比特位（一个字节）分为一个区间。

1.set

功能：将给定的数字对应的比特位数字标记为1。

关于数字的位置：我们怎么确定一个数字在第几个字节的第几个比特位呢？

其实很简单，因为一个字节是八个比特位的大小，所以 数字的字节位置 = 数字 / 8，数字的比特位位置 = 数字 % 8。

我们知道，0和1或上一个1，那么该位都为1。所以我们只需要把对应的位置或上1即可。

代码： 

void set(size_t x)
{//i表示在第几个字节,j表示在第几个比特位size_t i = x / 8;size_t j = x % 8;_bits[i] |= (1 << j);
}

2.reset

功能：将给定的数字对应的比特位数字标记为0。

如何做到保证其他位数字不变，特定位置的数字置零呢？

0和1与1都等于它本身，而0和1与0都等于0，所以我们只需要其他位与1，而对应的位置与0，即可做到置零。

void reset(size_t x)
{size_t i = x / 8;size_t j = x % 8;//与上的数字其他位都是1,为了让其他位保持不变//需要reset的位置与上0,为了让其置零_bits[i] &= (~(1 << j));
}

3.test

功能：判定给定的数字对应的比特位数字是否为1。

只需要该位与1，如果该位为0，与1后的数字为0。该位为1，与1后的数字不为零。

bool test(size_t x)
{size_t i = x / 8;size_t j = x % 8;return _bits[i] & (1 << j);
}

完整代码：

#pragma once
#include <vector>
namespace BitSet
{template<size_t N>class bitset{public:bitset(){//_bits.resize(N / 8 + 1, 0);_bits.resize((N >> 3) + 1, 0);}void set(size_t x){//i表示在第几个字节,j表示在第几个比特位size_t i = x / 8;size_t j = x % 8;_bits[i] |= (1 << j);}void reset(size_t x){size_t i = x / 8;size_t j = x % 8;//与上的数字其他位都是1,为了让其他位保持不变//需要reset的位置与上0,为了让其置零_bits[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 8;size_t j = x % 8;return _bits[i] & (1 << j);}private:vector<char> _bits;};}

三、位图的应用

1. 快速查找某个数据是否在一个集合中

2. 排序 + 去重

3. 求两个集合的交集、并集等

4. 操作系统中磁盘块标记

面试题：

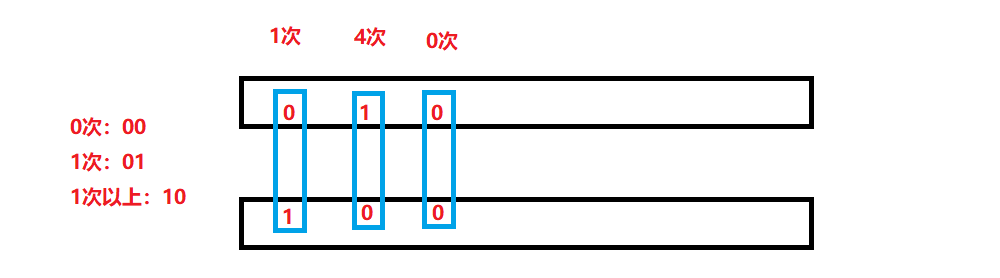
一个数字有三种状态：0次、1次、超过一次。所以我们需要用两个比特位来记录。由于用连续的两个比特位来记录会比较麻烦，我们可以开两个位图，各用一位来记录高位和地位。

这样就能复用我们的bitset了。 

代码：

template<size_t N>class twobitset{public:void set(size_t x){if (!_bs1.test(x) && !_bs2.test(x)) //00{_bs2.set(x);}else if (!_bs1.test(x) && _bs2.test(x))	//01{_bs1.set(x);_bs2.reset(x);}//10不需要管}void PrintOnce(){for (size_t i = 0; i < N; ++i){if (!_bs1.test(i) && _bs2.test(i)){cout << i << endl;}}}private:bitset<N> _bs1;bitset<N> _bs2;};}

思路也很简单，我们开两个位图，如果两个位图中的某一位同时为1，那么就是两个文件的交集。

注意：虽然是100亿个整数，但是整形最大范围还是42亿多，所以是不需要开100亿个空间的。

其实和第一题的解法一样，只不过现在需要多加一种状态，那就是超过2次的我们标记为：11。